前回、前々回のエントリーは何のためにアップしたかというと、発端はいつも読ませてもらっている id:kazuhotel さんの、このエントリーへの突っ込みでした。
重箱の隅つつきとか揚げ足取りとかが大好きな性格の悪い奴なので、さっそく次のようなあらずもがなのブックマークコメントを投入させてもらいました。
送電線の張り方? - デザインのはてな
高圧送電線は6本とか必ず3の倍数なんだぞー…と、本筋と全然関係ないところに突っ込み。
2015/12/19 10:32
しかしブコメを書いた後で、ふと考え込んでしまいました。工業高校、高専、大学などで電気を専攻した人間にとって、高圧送電線の本数が3の倍数になるのは、初年度早々に叩き込まれることなのですが、電気専攻ではない人すなわちほとんど大部分の人に、なぜそうなのかを説明するのは、意外に難事だと気づいたのです。それで、このネタで何かエントリーを書こうかなと思いながら、1ヶ月以上経ってしまいました。
スポンサーリンク
いくつか前提を。
まず初めに、電力は電圧と電流の積だということです。式で書くと…
P(:電力)=V(:電圧)× I(:電流)
となります。しかし、送電線には必ず損失があります。電気ストーブのように電力が熱となって放出されてしまうのです。このロスをPL、送電線の抵抗をRと書くと…
PL = I^2 × R
と、ロスは電流の2乗に比例します。従って送電線では極力、電圧を高く、電流を小さくした方がいいのです。電圧と電流の比率は、変圧器によって変えることができます。
しかし、電圧はいくらでも高くできるわけではありません。あまりに高すぎると、絶縁破壊というものがあって、空気中で放電してしまいます。
我々に身近なコンセントは、前回のエントリーに貼ったgifアニメの右側のような交流電圧を供給しています。この波形は、左側のように回転するベクトルの頂点を、y軸に射影したものと考えることができます。しかし紙の上にはアニメーションを描くことはできません。電気工学では「ベクトル図」と言って、原点を中心にベクトルを描き、それを頭の中で回転させて、射影した波形を電圧や電流としてイメージするのです。
なお日本の場合、周知のとおりコンセントの電圧は100Vです。これは「対地電圧」と言って、大地(アース)の電位を0Vとした電圧のことです。壁のコンセントをよく見ると、穴に大小の違いがあります。これは大きい方の穴が「接地」と言って大地に接続されていることを示しているのです。
発電所で発電した交流電力を送電するとき、電圧および電流の和を常にゼロにしなければならないという制約があります。このエントリーでは、電流の方は無視して電圧だけを考えます。仮に2本の送電線を使って電力を送電するとしたら、それぞれの送電線にプラスマイナスを逆にした対地電圧を発生させれば、対地電圧の和は常にゼロになります。このような送電方式を「単相送電」と言います。
単相送電のイメージを下のgifアニメで示します。右側の赤と青で示したグラフの平均は常にゼロになっていることがおわかりいただけると思います。ベクトル図では、左側のように、大きさが対地電圧の最大値に相当し向きが正反対のベクトルによって表すことができます。

二本の送電線の電圧の差を「線間電圧」と言います。下の静止画像に示す通り、各送電線の最大対地電圧をEとすると、線間電圧の最大値は2Eとなります。つまり二本の送電線の間には、最大で対地電圧の倍の電圧がかかるため、それだけ絶縁破壊が起こりやすくなるのです。
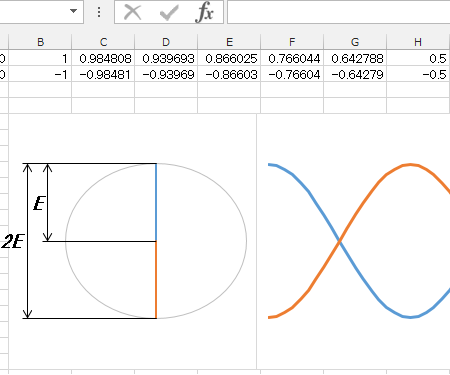
送電線を3本使用することを「三相送電」と言います。各送電線には、それぞれ位相を-120°、0°、120°ずつずらした電圧を発生させます。そうすると、三本の送電線の電圧の和は常にゼロになります。
三角関数の公式を覚えている方は sin(α+β)=sin α × cos β + cos α × sin β と sin 120° = √3/2、cos 120° = -1/2 を用いて証明することもできます。
各送電線の電圧を E sin(θ - 120°)、 E sin θ、E sin(θ + 120°)とすると、
E sin(θ - 120°)+ E sin θ + E sin(θ + 120°)
= E ( -1/2 sin θ + √3/2 cos θ + sin θ - 1/2 sin θ -√3/2 cos θ )= 0
と、θ に関わらず常にゼロになるのです。

三相送電には、どのようなメリットがあるでしょうか。下の静止画像をご覧ください。対地電圧すなわちベクトルの大きさをEとすると、線間電圧の最大値は、ご覧のように正三角形の一辺の長さに等しくなります。従って√3E ≒ 1.73Eと、単相送電の場合より約13%低く抑えることができるのです。
ベクトル図を用いる利点は、このように交流波形をトポロジーに変換して理解できることです。
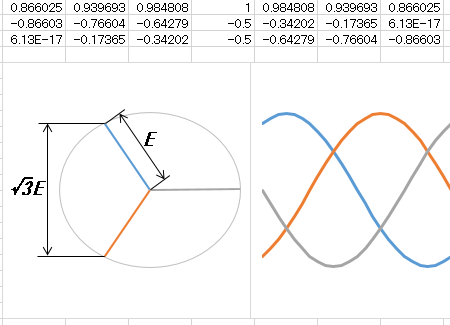
それでは送電線の数をもっと増やせばいいかというと、そうではありません。実は三相送電の場合が、線間電圧を最も低く抑えることができるのです。
仮に四本の送電線を使う「四相送電」というのを考えてみます。この場合、各送電線に位相を90°ずつずらした電圧を発生させると、電圧の和をゼロにすることができます(証明は省略します)。しかし線間電圧の最大値は、下記静止画像に示すように、正方形の対角線によって示すことができます。すなわち各相の対地電圧をEとすると、2Eと、単相送電の場合と同じになります。
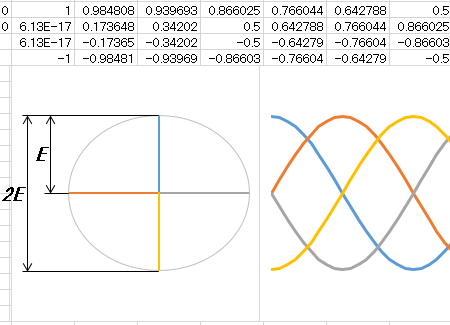
五本の送電線を使う「五相送電」というのがあったとしたら、各送電線に位相を 360° ÷ 5 = 72°ずつずらした電圧を発生させると、電圧の和をゼロにすることができます。しかし線間電圧の最大値は、下記静止画像に示すように、正五角形の対角線によって示すことができます。すなわち対地電圧をEとすると、中心角72°の sin を使って2sin72° × E となり、関数電卓を使うと2sin72° ≒ 1.90 と単相送電とあまり差がないことになります。
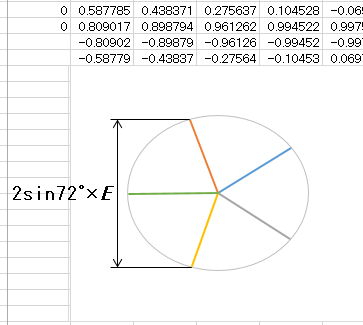
交流電力を送るには三相送電が最適だ、というのが結論です。実際には、万一断線があった場合のスペアのために三相送電を二組、すなわち送電線を六本使用するのが一般的です。
あんまりわかりやすくなかったですね。すみません。
追記:
別の応用例です。
スポンサーリンク