Excelに限らず表計算ソフトで掛け算と平均さえ計算できれば回帰直線くらいなら求められるんじゃないかな？（前編：導出編）

昨日の弊エントリーには多くのはてなスター、コメント、ブックマークコメントをいただき感謝しています。ブコメの一つに乗っからせてもらいます。我々が深淵を覗くとき深淵もまた我々を覗いているように、ブクマカーがエントリーを覗くときブログ主もブクマカーを覗いているのだ…って何を当たり前のことを（いらんことだがブクマカーというのは anonymous diary 通称増田の表記）。

Excel2013で回帰直線グラフを描いてみたらあまりの簡単さに30数年前の学生時代のあの苦労は何だったのかと情けなくなった - しいたげられたしいたけ

今だにMac用にExcel2008使ってるので統計処理できません．Mac用の安価で良い統計ソフト欲しいです・・・

2016/06/01 05:04

b.hatena.ne.jp

おまきざる （id:browncapuchin）さんのような優秀な人には、回帰分析などのツールは必要なときに道具としてサクっと使ってほしいんだけどな、という感想を抱いた。つか一連のExcelによる統計ネタで、タネ本として使っている本をまだ晒してなかったので、遅ればせながら晒してしまう。 

できるやさしく学ぶExcel統計入門 難しいことはパソコンにまかせて仕事で役立つデータ分析ができる本 できるシリーズ

上掲書はExcel2007、2010、2013対応を謳っている。Mac版2008はWindows版だと2007に相当するんじゃなかったっけ？ 違ってたらすいません。Excelの最新版は2016だが、丹念にチェックしたわけじゃないけどそっちでも使えると思う。

スポンサーリンク

それはともかく、前回のエントリーで扱った回帰直線くらいであれば、Excelのバージョンに関わらず、いやExcel以外の表計算ソフトでも、掛け算と平均の計算ができれば求められるんじゃないかなと思ったので、自分の勉強のためにエントリーを書いてみる。

まずは回帰直線を求める公式を導出してみる。前回はいきなりExcelの関数を使用して端折ってしまった。いくつか準備を。n個の変数x：x1、x2…xnの平均（相加平均）を5月27日のエントリーで使った画像の使い回しだけど、次式で与える。

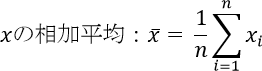
xの分散を、次式で与える。

標準偏差は、分散の正の平方根である。

変数xの他に、やはりn個の変数y：y1、y2…ynがあったとして、xとyの共分散というのを、分散と似た次式で与える。

xとyの共分散は、次の公式でも計算することができる。

証明は「高校数学の美しい物語」さんの「共分散の意味と簡単な求め方」をご覧ください。ただしあちらでは共分散をCov(X,Y)と表記しています。

共分散は、xの標準偏差sxとyの標準偏差syとともに相関係数rを求めるのに用いるなど、それ自体有用なものである。

相関係数に関する説明もまた、「高校数学の美しい物語」さんの「相関係数の数学的性質とその証明」をご覧ください。

「高校数学の美しい物語」さんをたびたび参照するなら、記号もそちらに合わせろよと言われそうだが、これまでずっと使ってきたタネ本『新確率統計』の記号に合わせているもんで。すいません。

いよいよ回帰直線の方程式を求める。回帰直線というのは、変数xとyの間にy=ax+bの関係が成り立つとして、xiから計算したaxi+bと実際のyiの差の二乗が最小になるよう、係数a、bを定めた直線である。すなわち次式のfを最小にしようという訳である。

そのためには、fをaとbの関数と見て、fのaとbによる偏微分がゼロになる条件を求めればよい。偏微分をとるときに変数変換を使っています。高校数学の範囲のはずです。

後半の式を変形して…

1項目はyの平均、2項目はxの平均にaを掛けたものになる。

前半の式を変形して…

両式からbを消去する。

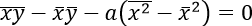
1項目と2項目はxとyの共分散の公式だ！ そして3項目はxの分散の公式にaを掛けたものだ！

だからaすなわち回帰直線の傾きを、共分散と分散の記号を使って書き直すと…

bすなわち回帰直線の切片は、yの平均、xの平均、およびaを用いて…

このような手法を最小二乗法というそうだ。なお以上の導出は、タネ本『新確率統計』P48～49のほとんどそのまんまです。説明を加えて多少はわかりやすく書けないかなと思ったのですが、むしろ改悪だったかも知れません。すいません。

昨日のエントリーに書いた通り、30何年かぶりに導出の過程を辿ってみると、複雑な数式が既知の公式に収斂してゆくさまが、こよなく美しいと感じた。しかし回帰直線の公式を「美しい」と評しているのを、よそで読むか聞くかした記憶はほとんどない。あるかも知れないけど私は知らない。

思うに回帰直線の方程式は、導出してから実際に応用するにあたって、膨大な計算が要求されるため、多くの人は計算間違いに苦しめられ「美しい」という感想を抱く暇がないんじゃないだろうか？ 計算ドリルで90点や95点を取れば「よくできました」と褒めてもらえるだろうが、正しい回帰直線を得るには100点満点以外は許されないのだ！

数学はよく登山に譬えられる。山道を自分の足で踏破した者だけが、頂上に立つ感動を味わうことができるという意味だ。しかし回帰直線の方程式の場合、頂上に立つまでは里山に登る感覚でも、下山ルートがいきなりアルプスの下山路に変わるようなものだろうか？ 頂上に立った感動を覚えている余裕はない。

「美しい数式」の代名詞といえば、オイラーの公式だろう。オイラーの公式も、導出の難易度はそんなに高くない。厳密な議論を要求されないのであれば、複素数とテイラー展開を知っていれば十分のはずだ。一方、オイラーの公式の応用も広範だが、電気工学であればベクトル図など応用にはワンクッション以上挟むため、オイラーの公式自体が呪詛の対象になることが少ないので「美しい」と評してもらえるんじゃないだろうか。

そんなことを、ふと考えた。

ちょっと長くなったので、Excelによる回帰直線の公式の計算は、次のエントリーで。

Microsoft Office Home & Business 2021(最新 永続版)|オンラインコード版|Windows11、10/mac対応|PC2台