Excelに限らず表計算ソフトで掛け算と平均さえ計算できれば回帰直線くらいなら求められるんじゃないかな？（後編：計算編）

前回のエントリー で導出した回帰直線の傾きと切片を求める公式を再掲する。

右辺の分子はxとyの共分散、分母はxの分散である。

右辺の第一項はyの平均、第二項はaとxの平均を掛けたものである。

スポンサーリンク

あえてExcelの関数を使わず代わりにこれらの公式を使って、前々回のエントリーの問題をもう一度解いてみる。グラフは作らない。

問題を再掲。大日本図書『新確率統計』P51から。

［問３］次の表は，ある森林から任意に選ばれた6本のパインの木について，幹の周囲x（単位m）と高さy（単位m）を測定したものである。

x	0.75	0.55	0.72	0.61	0.66	0.58
y	8.7	6.8	7.9	7.0	7.1	6.1

(1) y の x への回帰直線を求めよ．

(2) 幹の周囲が0.64mのパインの木の高さを，回帰直線を用いて推定せよ．

まずはExcelにデータを入力する。右の列に、xの二乗を求める式を入力する。

 さらに右の列にx掛けるyを求める式を入力する。

入力した式をまとめてコピーできるのはご存知ですか？（そういうウエメセ態度は反感しか買わないって＞自分

各列の平均、すなわちx、y、ｘの二乗、x掛けるyの平均を、まとめて求めることができるのもご存知ですか？（しつこいっつーの＞自分 

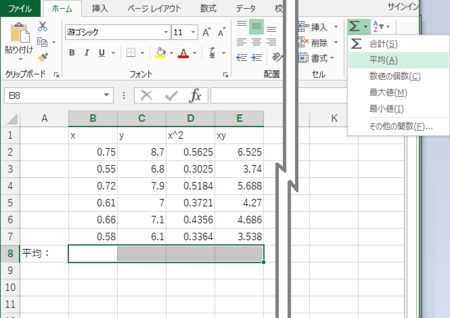
xの分散を、公式を用いて計算してみる。

xの分散を求める公式とは、「xの二乗の平均」－「xの平均の二乗」である（弊5/28付エントリー 参照）。

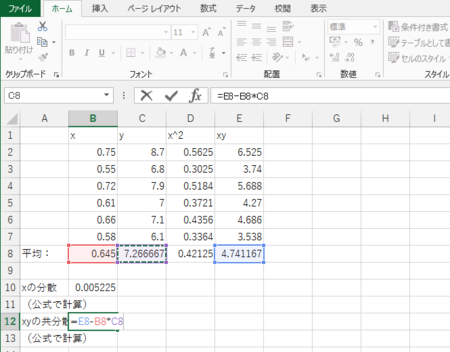
続いてxとyの共分散を、公式を用いて計算する。

xとyの共分散を求める公式とは、「x掛けるyの平均」－「xの平均掛けるyの平均」である（前回エントリー 参照）。

実はExcelには、xの分散を求める関数も、xとyの共分散を求める関数も用意されている。参考までに、関数を使った計算もやってみる。

[fx]（関数の挿入）ボタンをクリックし「関数の検索(S)」に「分散」と入力すると、候補が表示される。Excel2010以降であればVAR.P、Excel2007であればVARPを使用する。Excel2010以降のVAR.S、Excel2007のVARは、不偏分散を求める関数なので結果が異なる（インプレス『やさしく学ぶExcel統計入門』P233など参照）。

「関数の引数」ダイアログボックスより、xの入力されている範囲をドラッグで選択する。

同様に共分散を求める関数を検索する。Excel2010以降であればCOVARIANCE.P、Excel2007であればCOVARを使用する。COVARIANCE.Sは、標本の共分散を求める関数なので、結果が異なる。

引数としてx、yが入力されている範囲をドラッグで選択する。

公式を用いて計算した結果と、Excel関数を用いて求めた結果が一致している。当然とは言いながら。

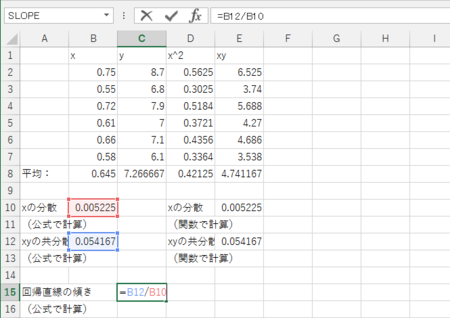
では、いよいよ回帰直線の方程式を求める。まずは回帰直線の傾きを、「xとyの共分散」÷「xの分散」によって求める。

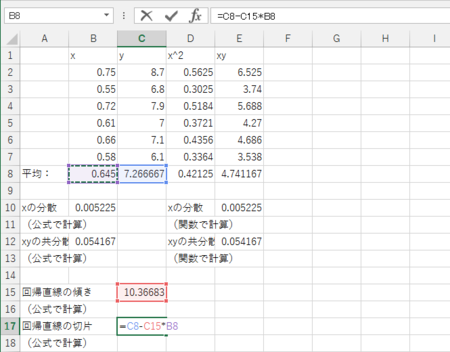
続いて回帰直線の切片を、「yの平均」－「回帰直線の傾き」×「xの平均」により求める。

参考までに、回帰直線の方程式もExcelの関数によって求めてみる。6月1日のエントリーでやったことと全く同じである。回帰直線の傾きは、SLOPE関数で求めることができる。

回帰直線の切片は、INTERCEPT関数で求めることができる。

今回も当然ながら、両者の値は一致している。

まとめると、回帰直線の方程式を求めるには、掛け算と平均しか使わなかったということだ！ 今回はやらなかったが、標準偏差を求めるにしても、新たに必要なのは平方根だけだ。だとしたら、Excelの古いバージョンでも、Excel以外の表計算ソフトでも、統計処理のかなりのことができるんじゃないだろうか？

なお回帰直線に関しては、白いケモノ （id:houyhnhm）さんから興味深い指摘をいただいていますので、感謝しつつリンクを貼らせていただきます。

abyss.hatenablog.jp

単回帰分析の場合、従属変数Yと説明変数Xの意味が異なる。Yは一定ブレ（残差）が生じるがXはブレを想定していない。
「見た目で何となく引く線」とは異なるのはその為である。
直線に対しての「距離」の最小化、とはならない。ここらへん、XとYを入れ替えても問題ない相関とは異なる。

前回までのエントリーで「美しい」と強調したけど、「計算が簡単だからよく利用されているだけ」という解釈も成り立ちそうです（あ、計算が簡単というのは導出が簡単という意味です。計算間違いに苦しめられたことは、くどいほど繰り返しました）。

Microsoft Office Home & Business 2021(最新 永続版)|オンラインコード版|Windows11、10/mac対応|PC2台