ホッテントリに、こんな「はてな匿名ダイアリー」(以下、通称の「増田」と書く)が上がっていた。
この話題、定期的に上がるんだよな。増田に限って言えば、一昨年の「0.999999・・・ってさあ」 「だったらπrもダメってことじゃん」 が同趣旨だった。今回のは、可愛げって点で、これらに負けてると思うぞ。
スポンサーリンク
だけど、読み返すと、この斬り込みは面白かったかな。
先生「例えば,0.333 の場合で考えてみましょう.これを 3 倍したら 0.999 ですよね?
0.3333 の場合は 3 倍すると 0.9999 です.これは 0. のあとに 3 が何個ある場合でも成り立ちます」
中学生「ちょっと待って下さい!確かにそうですが,それは 0. のあとの 3 の数が 3 個とか 4 個とか,
もっと多い場合,例えば 100000 個ある場合ですよね?
一方,この表記法は 0. のあとの 3 の数が ◯◯個あるとはいえません.
だから,それに 3 倍するって計算はできないんじゃないでしょうか?
実際,0. の一番右側の 3 がないから,筆算ができません」
先生「ぐぬぬ」
要するに、無限小数に四則演算が適応できるかは、保証の限りではないのだ。いやこれも「だったらπrもダメってことじゃん」と、言い回しが違うだけで同論旨かな?
ときに、上掲増田のブコメ欄には、予想通り「ε-N〔イプシロン-エヌ〕論法」または「ε-δ〔イプシロン-デルタ〕論法」で証明できるという旨のブコメがいくつも現れた。まあそうだろうと思う。
実は、上掲増田とは全く関係のない個人的事情であるが、最近、ちょっと驚いたことがあった。
とある大学の共通科目(昔でいうなら教養課程かな? 大学によって呼び方は違うだろうと思うけど)で使用されている微積分の教科書を見る機会があった。つか今はそれを使って、微積分の再勉強をしている。
大学数学のスタンダードだと思っていた「ε-N」の説明が、この教科書からは、すっぽり欠落していたのだ。
だからもちろん、あの懐かしい「デデキントの切断」に始まる4定理(すなわちその正体は「実数の公理」であるのだが)もない。
数学専攻とかバリバリ理系のクラスであれば、そんなことはないと思うのだが。
じゃあどうしているかというと、「極限値の性質」として次の4公式を掲げ、これらを公理のようにして、微分の諸定理を導いているのだ。
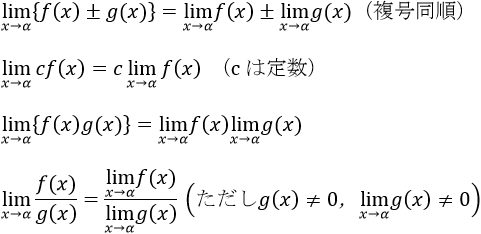
なるほどこれはこれで一つの手だな、とは思った。つか、「ε-N」を用いてこれらの公式を証明したかつての苦労は何だったんだ?
恨みを込めてあら探しをすると、果たして少し後の方で、合成関数の微分法の公式を求めるところで…

とやって…
(注) 条件 Δu ≠ 0のもとで公式を導いたが,この仮定がなくても証明できる.
などと書いてあった。仮定なしで証明するには ε論法が必要なのだ。
元の増田に話を戻すと、「0.999999... = 1」は、つまるところ実数の公理なのだ。
「ε-N論法」を用いて、デデキントの切断に始まる4定理に帰着させるのが、80年前の名著『定本 解析概論』にさかのぼる解析学のスタンダードなのだが、つまるところは約束事なのだ。証明はできない。証明できないことが証明済みなのだ。
もっと言うと、元の増田では、増田の作者が登場人物の中学生の肩を持って、中学生に教師をやり込めさせようとしていることがうかがえる。大学でまともに勉強した教師であれば、この程度で閉口することは、まずなかろう。
もし中学生が、教師の揚げ足をとるつもりで質問しているのであれば、教師は中学生にとって未知の概念をつぎつぎと繰り出して、煙に巻くことは容易であろう。人間は誰しも、自分の知らないことをいきなり持ち出されると、とっさには対応できないものである。
例えばこんな調子で…
先生「君はある演算を行ってその逆演算を行ったら、必ず元の値が得られるという前提で話をしているんじゃないか? 数学では、そんな保証は一切ないんだよ」
中学生「そんなことがあったら、計算がめちゃくちゃになってしまうじゃないんですか?」
先生「めちゃくちゃになろうがなるまいが、現にそういうことがあるのだから仕方がない。例えば大学数学だが、フーリエ級数という、幅広い応用範囲を持つ技法がある。関数の知識になるが、1を0.9+0.09+0.009+…に分解するのと似ていなくもない。ところがフーリエ級数から元の関数を復元しようとすると、ギブスの現象というのが現れて、原理的に不可能だということがわかっているのだ」
中学生「…」
…不毛だよね。
そうでなくて、もし中学生が、知的好奇心に基づいて質問をしているのであれば、そして、いくら時間をかけてもいいのであれば、中学生を飽きさせないだけの面白い話ができるんじゃないかと思う。
私にそれができるか、チャレンジしてみたい気もする。つまり、実数の公理とε-N論法が、なんで必要になるか、それらを使うと何ができるかを、できるだけやさしく自分なりに書いてみたい気がする。
ただし、よく書いているように、一つのエントリーに盛り込める情報量というのは、書籍に換算するとせいぜい1ページか2ページにすぎない。
それどころか、たくさんのアクセスと300を超えるブコメをいただいた下記弊エントリーに至っては、タネ本の1問を書き直したものに過ぎないのだ。
続編のこれが2問分だ。
実数の公理とε-N論法から、さきの極限値の4公式を導くのに、だいたいどの本も1章分くらいを費やしている。
完結させられるのか?
ちなみに、元増田のブコメ欄には、結城浩先生の『数学ガール』シリーズを薦めるブコメもいくつかありました。1巻だけは持っているものの、載っていなかったので検索したら、ε-δが論じられるのは3巻とのこと。未読です。結城先生すいません。読んでみなければ。

数学ガール/ゲーデルの不完全性定理 (数学ガールシリーズ 3)
- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2009/10/24
- メディア: 単行本
- 購入: 37人 クリック: 930回
- この商品を含むブログ (148件) を見る