なんだか急にひらめいたので、今やってる話題はひとまず措いて、先にこちらを書きます。
ネットで仮想通貨の話題が盛り上がっています。「えっ、この人も?」という意外な人までが、投資に参入しているようです。あくまで個人の感想です。また本人に直接そう言ったわけではありません。
他人の判断に口を出すのはヤボというもので、本来「ご健闘をお祈りします」以上のことを言うべきではないのでしょうが、どうにも危うさを感じないではいられません。投資というジャンルは、とうの昔から数学やAIを駆使した専門知識のカタマリになっており、素人が予備知識なしに参入しても、カモにしかならないのではないかと考えるからです。
ときに、以前こちらのホッテントリを見たとき、グラフの形状に共通の特徴がみられるように感じたので、簡単な数学モデルでシミュレートできるのではないかというアイデアを抱きました。
bitFrier さんより、本日(12/26)17:30時点のグラフをサンプルとしてお借りします。

ビットコイン(Bitcoin)価格・相場・チャート【bitFlyer】 より
グラフの立ち上がりは、指数関数を髣髴とさせます。自然界においてグラフが指数関数に似た曲線で増加するパターンは、実はそんなに多くありません。その代表的なものが「飽和曲線」または「ロジスティック曲線」です。ウィキペディアの記事は、こちらです。
また 迫 佑樹(id:McG)さんが、ブログ読者数のシミュレーションに応用した記事が、ホッテントリになったことがありました。
変数名を 迫 さんの記事に合わせた微分方程式を、下記に示します。
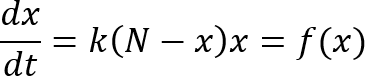
N は元記事では潜在的な読者数ですが、今回の拙記事では仮想通貨に投資される資金の総額と考えることにします。具体的な数値はわかりませんが、一定の上限がある(無限ではない)ことは自然な想像であるはずです。k は比例定数です。
それを今回は、次のように改造します。一定のタイムラグ Δt が存在すると仮定するのです。レートを見てから売買手続きが完了するまでは、どうしたって有限の時間がかかるからです。

これを今回は、解析的に解くのではなく、数値シミュレーションによって解いてみました。解法は「オイラーの方法」と呼ばれる折れ線近似です。すなわち

とします。h は「刻み幅」と呼ばれる定数です。上式を「式(1)」と呼ぶことにします。n はゼロ以上の整数で以下同じです。x0 は初期値です。
近似式の出典は、洲之内治男『数値計算 (サイエンスライブラリ理工系の数学)』P28です。私が使用したのは初版1978(S53)の古い本ですが、新版が出ているようです。
この h を遅延時間にそのまま転用します。 刻み幅と遅延時間には本来別の変数を用いるべきですが、手軽な数値実験ということで、今回はこれで進めます。すなわち Δt = h とした場合を

により計算します。上式を「式(2)」と呼びます。
また Δt = 2h とした場合を

により計算します。上式を「式(3)」と呼びます。
N および k の値は、深い意味なく 前記 迫 さんのエントリー の数値を借用し、N = 1000 、 k = 10^-5 = 0.00001 としました。そしてグラフのカーブが目視で上掲ビットコインのチャートに近くなる h の値を、試行錯誤により探しました。
ツールには Excel を使用しました。データの試行錯誤による再計算とグラフのリアルタイム描画に適しているからです。
下記スクショにおいて、セルC2、C3~D3、C4~E4 には x0 すなわち初期値として数値データ1を入力しています。
またセルD2、E3、F4 には 、以下の数式をそれぞれ入力し、行方向にコピーしています。それぞれ式(1)~(3)に対応します。セル$B$6は N、$B$7は k、$B$8は h の値が入っています。
| D2: | =C2+$B$8*$B$7*($B$6-C2)*C2 |
| E3: | =D3+$B$8*$B$7*($B$6-C3)*C3 |
| F4: | =E4+$B$8*$B$7*($B$6-C4)*C4 |
h =100 としたときに、ビットコインのチャートと似た形状の折れ線グラフが現れました。

式(1)すなわち遅延時間なしの場合が青色のグラフで、これは飽和曲線(ロジスティック曲線)になります。
式(2)すなわち遅延時間 h の場合がオレンジ色、式(3)すなわち遅延時間 2h の場合が灰色のグラフになります。N すなわち市場への資金供給の総額を越えたオーバーシュートが現れるのが特徴です。
灰色のグラフはマイナス値までアンダーシュートしています。仮想通貨にマイナスの値段がつくことはありえないので、より精密なシミュレーションを行うためには、モデルに修正を加える必要があります。
時間軸を、少しずつ増やしてみます。指数関数なので、一気に値が変化します。式(2)すなわちオレンジ色のグラフが周期変動していることと、式(3)すなわち灰色のグラフがマイナス域に侵入するのが特徴的です。

さらに時間軸を増やしてみます。灰色のグラフのマイナス値が一気に増加することが特徴的です。念のために繰り返しますが、現実にマイナスの値段がつくことはありえないので、あくまでシミュレーション上の現象です。

この灰色のグラフに「バブル崩壊曲線」という名前をつけてみたいなんて思うのですが、いかがでしょうか?
なおこのようなバブルの崩壊は、遅延時間を大きくしたときだけでなく、比例定数 k を大きくしたときにも現れます(ただし遅延時間がゼロでない場合)。
* * *
以上の、ごく初等的な数値シミュレーションの結果を踏まえて、仮想通貨の今後の値動きに関して考察してみます。
まず第一に、仮想通貨の値段が、今後ずっと指数関数的に増加することはありえません。このことは100%の確信度をもって断言できます。投資資金の総額は無限ではないからです。つまり今から仮想通貨市場に参入しても、いわゆる「億り人」になることは不可能と覚悟しておいたほうがいいと考えます。
第二に、かと言って必ずしもバブルが崩壊し、仮想通貨が無価値となるとは限らない、とも言えそうです。「市況かぶ全力2階建」記事中のミシシッピ・バブルや南海バブルの時期と比べて、今日の取引に関わる遅延時間は、大幅に短縮されているはずだということと、何度ものバブル崩壊の経験を経て、市場自体も昔に比べて賢くなっているはずだと思われるからです。ただしこの命題に関する確信度は、若干下がります。バブルが崩壊する可能性はゼロだとは断言できません。
けっきょく仮想通貨の価値は、今後ある一定の値段を中心に増減を繰り返すことが、一番ありそうに感じられます。だから、市場価格が割安なときに購入して割高なときに手放すということを繰り返せば、儲けを出すことは可能のはずです。ただしこの操作は、仮想通貨以外の株、先物、有価証券の取引と本質的になんら変わるところはありません。
さらにもう一言言うと、例えば今回Excelに描かせたグラフを現実のチャートと重ね合わせるだけでも、N すなわち市場に流入している資金の総額や、k すなわち取引価格の変動周期を予測するのに利用できる比例係数の、おおざっぱな値を知ることができるのです。
機関投資家やプロのトレーダーは、口には出さなくとも必ずやもっと精密なシミュレーションを行っているに違いありません。金融工学のことはよく知りませんが、デジタル制御工学においては、オブザーバと言って精緻な理論が古くから確立しているのです。今日ではAIがそれに加わっていることでしょう。
そういう人たちを相手に、知識のない素人が運だけを頼りに徒手空拳で立ち向かって、勝てると思いますか?
それでもチャレンジしてみたいと考える人には、「幸運をお祈りします」とだけ申し上げることにします。
スポンサーリンク
