前回のエントリー の続きです。前回のあらずじは、仮想通貨の上昇曲線が指数関数カーブに似ているので、理系にはおなじみのロジスティック方程式
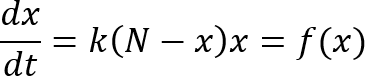
を、遅延時間を加味してこんなふうに改造し、

Excel で折線近似による簡単なシミュレートを行ったら、バブルの崩壊らしきものが観察できた、ということです。以後、この式を「バブル崩壊方程式」と呼んでみる。
* * *
それからさらに、数式をいろいろいじってみた。
まず「バブル崩壊方程式」では、仮想通貨の価格 x がマイナスになるのが気になる。マイナス値が指数関数的に激増する現象は面白かったが、それがなんら現実を反映するものではない。
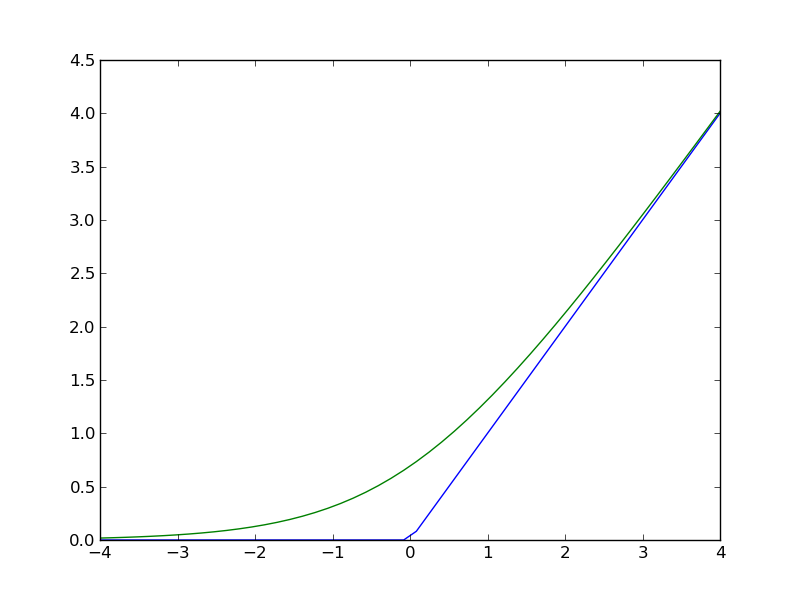
そこでまずは、これも理系にはおなじみの ReLU関数 というのを当てはめてみた。活性化関数 の一種として知られている。
Wikimedia Commons より。CC0 だったので感謝しつつお借りします。
青線グラフがReLU(ランプ関数)、緑線グラフはソフトプラスと呼ばれるやはり活性化関数の一種で、あとで出てきます。
セルと各定数の数値は前回と同じ。数式は if 関数を使って、次のように実装した。
| D2: | =C2+$B$8*$B$7*($B$6-C2)*C2 |
| E3: | =IF(D3+$B$8*$B$7*($B$6-C3)*C3>0,D3+$B$8*$B$7*($B$6-C3)*C3,0) |
| F4: | =IF(E4+$B$8*$B$7*($B$6-C4)*C4>0,E4+$B$8*$B$7*($B$6-C4)*C4,0) |
D2は遅延なし(ロジスティック方程式)、E3は遅延 h 、F4は 遅延 2h の数値を求める数式で、それぞれ行方向にコピーした。h と Δt は本来別の変数にすべきだが、簡易的な数値実験ということで同じにしてしまったのも前回記事と同じ。
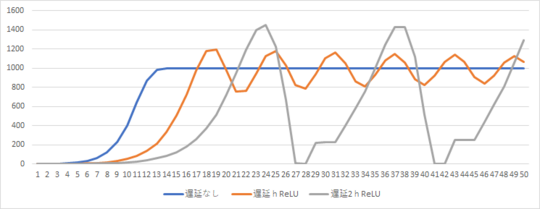
遅延 h(オレンジ色グラフ)は、マイナスの値を取らないので、結果は前回から変化はない。
遅延2h(灰色グラフ)には変化が現れたが、マイナスの部分が折り返され振幅の大きい周期になっただけのように見える。「より現実に近づいた」とは、とても言えそうにない。
スポンサーリンク
思いて学ばざれば則ち殆〔あやう〕し、ロジスティック方程式に遅延時間を加味するくらいの改造は、誰かとっくに思いついているはずだと思って、少し探してみた。
他ならぬウィキペディアの「ロジスティック方程式」の下の方に、ハッチンソン方程式というのが載っていた。ウィキぺなかなか全部読まないんだよね。関数名と変数名を前回記事に合わせて書き直すと、こんな形になる。
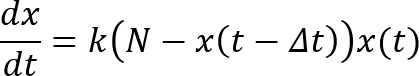
自称「バブル崩壊方程式」と比較すると、一行目の右辺に出てくる2番目の (t-Δt) が t に変わっただけだ。
Excel の数式実装は、すげー楽だった。セルE3が自称「バブル崩壊方程式」、F3がハッチンソン方程式。違いは最後に乗算するセルだけである。文字に彩色して示した。
| D2: | =C2+$B$8*$B$7*($B$6-C2)*C2 |
| E3: | =D3+$B$8*$B$7*($B$6-C3)*C3 |
| F3: | =D4+$B$8*$B$7*($B$6-C4)*D4 |
オレンジ色の折れ線(ラベル f(t-Δt))が自称「バブル崩壊方程式」、灰色の折れ線(ラベル f(t, Δt))がハッチンソン方程式の描くグラフである。灰色のグラフはオレンジ色のグラフに比べて、立ち上がりが飽和曲線に近づいていることと、オーバーシュートおよび振幅が大きくなっていることが確認できる。
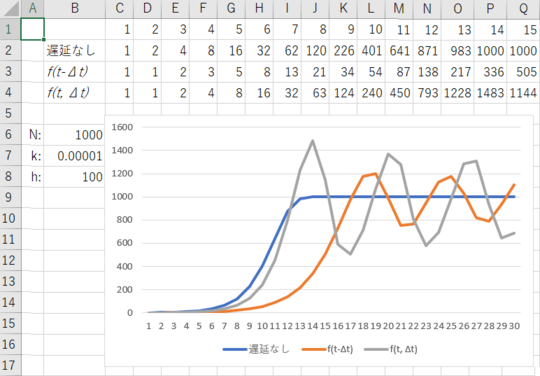
さらにハッチンソン方程式によるグラフには、ReLU関数によるマイナス値の切り捨てを行っても、周期変動が現れないという特徴が見られた!
| D2: | =C2+$B$8*$B$7*($B$6-C2)*C2 |
| E3: | =D3+$B$8*$B$7*($B$6-C3)*C3 |
| F3: | =IF(D4+$B$8*$B$7*($B$6-C4)*D4>0,D4+$B$8*$B$7*($B$6-C4)*D4,0) |
今回はオレンジ色がハッチンソン方程式のグラフ、灰色がハッチンソン方程式のマイナス値をReLU関数で切り捨てた場合のグラフである。アンダーシュートが現れるよう、h = 129 としている。その他の定数の値は、以前と同じだ。
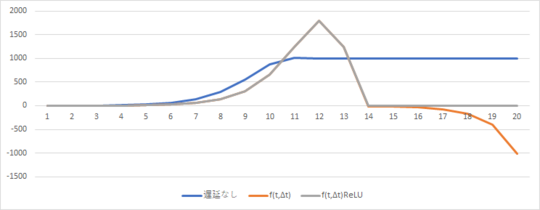
これにより、過去のバブル崩壊時に現れた曲線に、やや近づいたようには見える。だが正直「だから何なんだ?」という感もある。
スポンサーリンク
せっかくだから、もう少しいじってみた。関数の値が不連続にゼロになるというのも不自然に感じたので、前に述べたソフトプラス関数というのを使って、ゼロ付近の丸め方を滑らかにしてみた。
ソフトプラス関数というのは、こんなのである。グラフは先に示した(いずれも「活性化関数 - Wikipedia」より)。
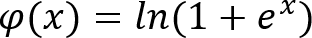
x → +∞ で φ(x) = x、x → -∞ で φ(x) = 0 となるのが特徴である。ただし Excel で EXP を計算させるとオーバーフローエラーが生じるので(正確にはEXP関数の結果をLN関数の引数に入れるとエラーになる)、実装に当たっては IF 関数で x がある値を越えたらφ(x) = x とする工夫を行った。数式は少し煩雑になったので省略する。
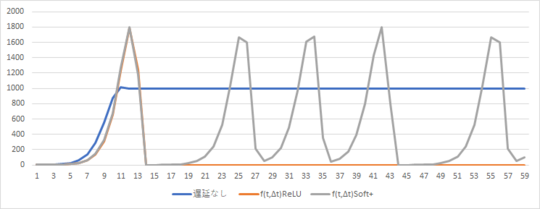
青色グラフが飽和曲線、オレンジ色グラフがハッチンソン方程式+ReLU関数、灰色グラフがハッチンソン方程式+ソフトプラス関数である。各定数の値は、一つ上のグラフと同じものを使用している。
灰色のグラフにおいて、ピークが非周期的に表れるのが特徴である。これは害虫の異常発生やインフルエンザのようなパンデミックが、非周期的に起きることのシミュレーションになっていないだろうか?
* * *
というわけで、仮想通貨市場を我流で数値シミュレーションしようとしたら、結果的に生物学の勉強をしたみたいなことになってしまった。これはこれで面白かったから、自分用に記録を残す。金融工学は金融工学として勉強した方がよさそうだ。つか、そうに決まっている。まこと「思いて学ばざれば則ち殆し」である。
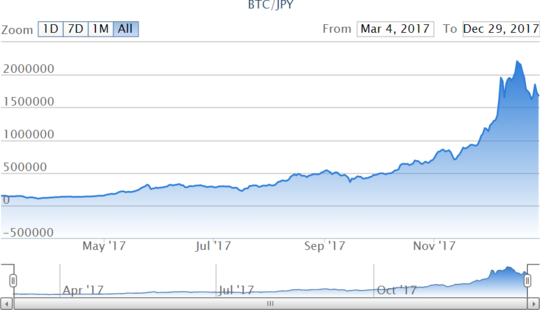
全くの蛇足ではあるが、現実のビットコインのレートは、12月29日13:00現在、こんなふうになっていた。前回同様 bitFrier さんよりお借りします。多分しばらくはボックス相場だろうな。
スポンサーリンク