ハッチンソン方程式のグラフが「バブル崩壊曲線」を描くか否かはピーク値によって決まる？

いつもの悪い癖で、もっと早く書こうと思いながら、気づいたらずるずると半月以上経ってしまった。

Twitter への言及がここのところ多いが、今回はタイムラインにこんなリツイートが流れてきたことがきっかけだった。FF外から引用失礼します。

わろた pic.twitter.com/y6NbQcDaaT

— もちベーコン (@qxqxqxaqua) 2018年1月14日

この画像自体は出所不明、真偽不明のデータと言わざるを得ないのだが、これを見たとき個人的には「はっ」と気づくことがあった。

去年の12月に、こんなエントリーを書いた。

watto.hatenablog.com

この拙記事で言いたかったことは、指数関数的に増加するグラフは、簡単な数値シミュレーションによると

ケース1. 一定値に収束する、すなわち飽和するか… 

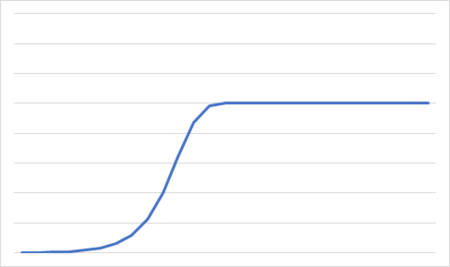
ケース2. 一定値を中心に増減を繰り返す、すなわちボックス相場となるか… 

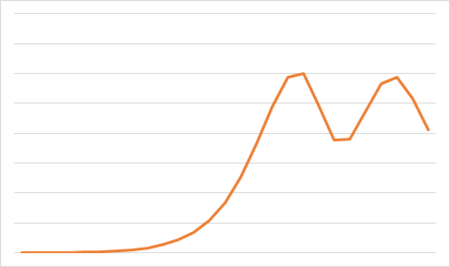
ケース3. アンダーシュートが発生する、すなわちバブル崩壊するかのいずれかで… 

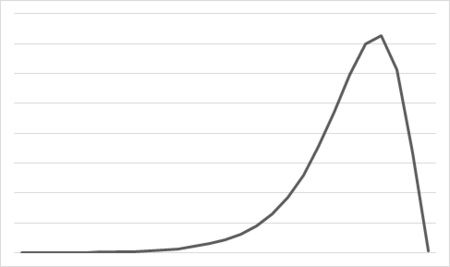
要するに永遠に指数関数的増加を続けることはありえない、ということだった。

だいたい57垓〔がい〕なんて現金が、地球上のどこにあるというんだ？ もし全額換金したら、たちまち世界中がハイパーインフレだ。

しかしそれでも止まることはないのだ。Youtube で有名になったビデオ “Powers of Ten” を思い出さざるを得ない。かりに観測可能な宇宙を1万円札で埋め尽くしたとしても、もし仮想通貨の含み益が指数関数的増加を続けるのであれば、やすやすとその額を突破するであろう。

Powers of Ten™ (1977)

しかし去年の12月の時点では、それでは仮想通貨が今後、ボックス相場となるかバブル崩壊するかの判断は避けた。これ以上手持ちのデータがないと思ったからだ。

だが上掲のツイートを見たとき、判断材料となる手がかりがもう一つあることに、遅まきながら気づいた。

Excelを使った簡易な数値シミュレーションとは言え、シミュレーションを繰り返すうち、グラフがボックス相場を描くかバブル崩壊曲線を描くかは、オーバーシュートの大きさによって決まるのではないかと思ったのだ。ここで言う大きさとは、収束する場合の一定値に対する比率のことだ。

スポンサーリンク

Excelは手軽とはいえ、精度を上げようとすると必要とするセルの数が膨大になるなど扱いにくくなるので、プログラム言語を使うことにした。今の私の環境ですぐに動かせるのは Python だけなので、不慣れを押してコードらしきものをでっち上げてみた。

ハッチンソン方程式の元の数式を再掲。

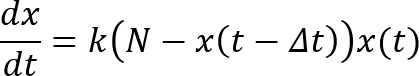
これを、去年の12月26日付エントリー と同様「オイラーの方法」すなわち折線近似で実現するため、次のようなコードにしてみた。

スクリーンからのコピペでも実行できることは確認した。Python のバージョンは 3.6.0 である。

import numpy as np
import matplotlib.pylab as plt
h = 0.01
k = 1.0
N = 10
dt = 5
step = np.arange(200)
t = h * step
x = h * step
for i in step:
    if i <= dt:
        x[i] = 0.1
    else:
        x[i] = x[i-1] + h*k*(N-x[i - dt -1])*x[i - 1]

plt.xlabel("t"), plt.ylabel("x(t)")
plt.plot(t, x)
plt.show()

ゲイン k = 1、飽和値 N = 10 という各定数の値は仮に決めたもので、特に意味はない。グラフの形を見ることが目的である。

遅れ時間 dt = 0 の場合は、ロジスティック曲線（飽和曲線）になる。

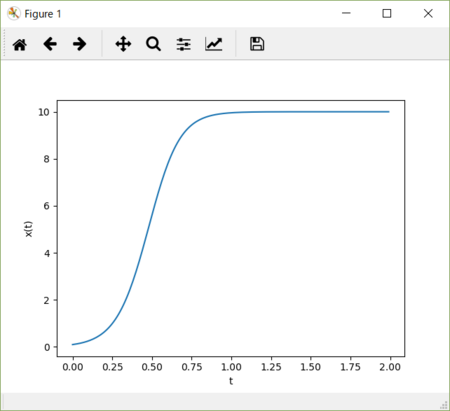
ゲイン k = 1、飽和値 N = 10 はそのままで、遅れ時間 dt = 5(×0.01=h) の場合のグラフ。すなわち上掲コードをそのまま貼り付けたときの結果は、こうなるはずだ。

プログラムの都合上、遅れ時間 dt は整数と刻み幅 h の積で表現している。

遅れ時間が非零の正値である場合、オーバーシュートが発生する。

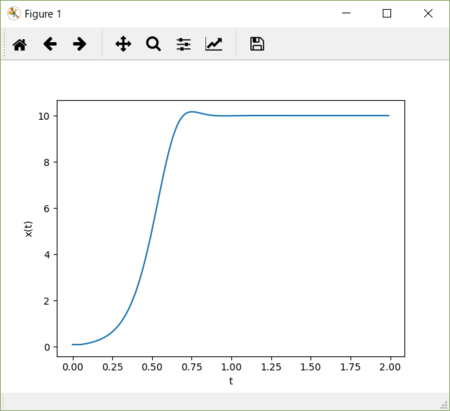
他の定数の値はそのまま dt = 10 とした場合。オーバーシュートの量が増大する。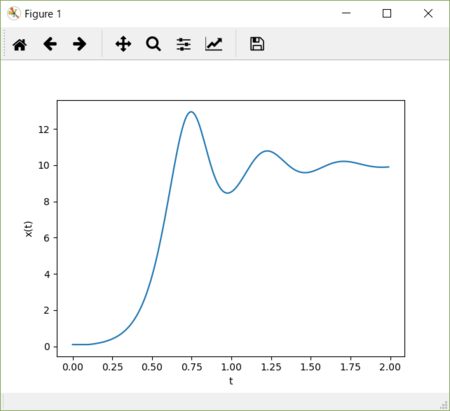

dt = 15 のグラフ。振幅がさらに増大する。

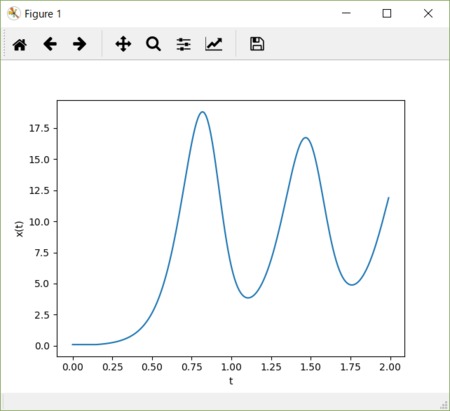
dt = 20。振幅の下限が横軸すなわちゼロに接近する。

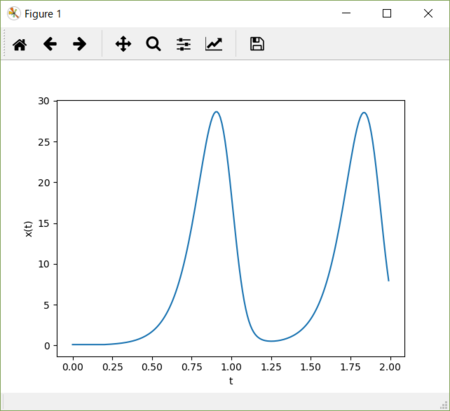
dt = 25。下限が横軸に接触しているように見える。

Excelによる近似計算では、すでにアンダーシュートが始まっている値だが、Excelの近似は刻み幅 h ＝0.1 とあまり小さく取らなかったので、誤差が大きかったのかも知れない。

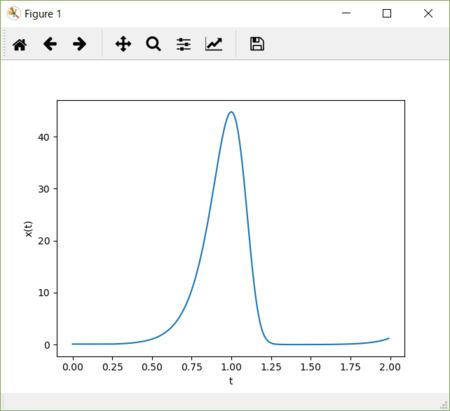
dt = 30。横軸（t軸）をもっと先まで取ると、アンダーシュートが観察される。

ということは、アンダーシュートの発生は、数式の本質的なものか（解析的に出現を示せるものか）、それとも近似誤差によるものかという検討も必要になりそうだが、今後の課題としよう。

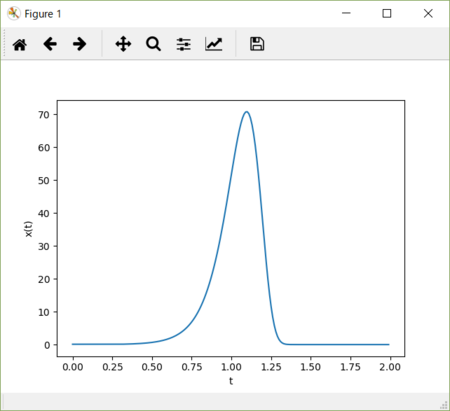
なお N、k を変更した場合も、グラフのスケールすなわち縦軸と横軸の比に変化は生じるものの、グラフの形状としては共通したものが現れる。

飽和値 N = 10 はそのまま、ゲイン k = 0.5、遅れ時間 dt = 10とした場合のグラフ。

横軸の方向に間延びしているが、k = 1、dt = 5 のグラフと似ている。

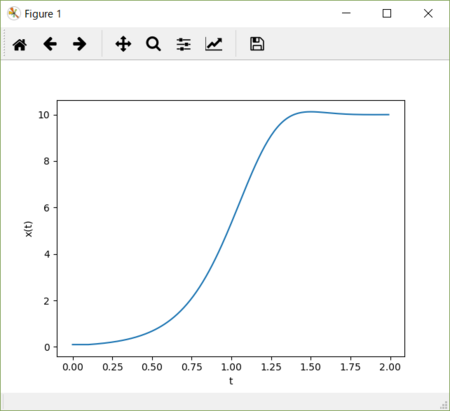
k = 1.5、dt = 10 のグラフ。今度は横軸方向に圧縮されているが、k = 1、dt = 15 のグラフに似ている。特にピーク値がほぼ同じだ。

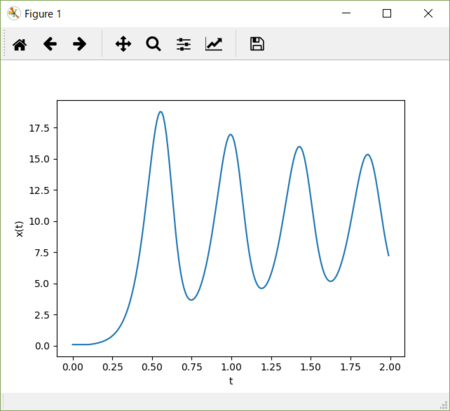
k = 2.0、dt = 10 のグラフ。横軸方向にさらに圧縮されているが、k = 1、dt = 20 のグラフに似ている。やはりピーク値がほぼ同じである。

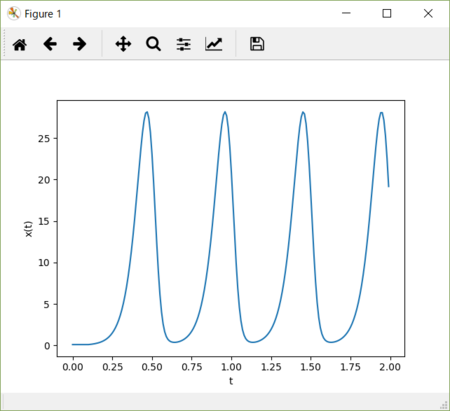
実はハッチンソン方程式の定数 N、k、dt のうちどれか一つの定数の変化に関しては、t、x を適切な t’、x' に変数変換することによって、他の定数を変化させた式と同じ形にすることができるのだが、煩雑になるのでこの記事ではその議論は省略する。

ここで言いたいことは、ハッチンソン方程式を用いたモデルにおいては、オーバーシュートの大きさ（Nに対する比）によって、グラフが増減を繰り返すかアンダーシュートが生じるかの予測ができるはずだということだ。

そして結果を分けるオーバーシュートの値は、今回のハッチンソン方程式モデルを用いた簡易な数値シミュレーションによると、だいたいNの5～7倍のようだ。もう少し絞り込めるかも知れない。

スポンサーリンク

さて、最初のツイートの話に戻る。もしも本当にビットコインの含み益が垓の桁に達しているのであれば、レートにマイナスはないので、ビットコインの今後のレートはバブル崩壊曲線のコースをたどるだろう。

ではビットコインの時価総額は、現実に近い値としてはどのくらいになっているのだろう？ これはビットコインの発行量とレートの積によって簡単に計算できる。

検索して出てきた数字によると、ビットコインの2017年末の発行量は約1,600万BTCとのこと。レートは目下変動が激しいけど、1BTC≒ 100万円とすると、時価総額は約16兆円となる。

これが市場規模として適正と言えるだろうか？ 総務省のサイトによると、日本の産業別の市場規模は、2014(H26)年の数字で鉄鋼 約23兆円、電気機器（除情報通信機器）約31兆円、輸送機械 約52兆円、建設（除電気通信施設建設）約52兆円、卸売 約57兆円、小売 約38兆円…とのことだった。詳細な数字は次のリンク参照。

総務省｜平成26年版 情報通信白書｜日本の産業別実質市場規模（国内生産額）の推移

あるいは株価の時価総額で近い数字を探すと、Yahoo! ファイナンスの時価総額（最終更新日時：2018年2月2日）の数字で上位からトヨタ自動車 約25兆円、三菱ＵＦＪフィナンシャル・グループ 約12兆円、日本電信電話 約12兆円、ＮＴＴドコモ 約11兆円、ソフトバンクグループ  約10兆円…これもソースへのリンクを示す。

時価総額上位：株式ランキング - Yahoo!ファイナンス

その他、ビットコインへの投資家数を概算して時価総額を投資家数で割ってみるなど、簡単に入手できるデータをいくつか集めてみた。

結論だけを書くと、もちろん正確なことはわからないが、ビットコインのレートに関する限り、レートのグラフのオーバーシュートすなわちピーク値は、適正値（もしそんなものがあるとするならば、だが）より少なくとも桁が2つか3つ大きいのではないか、という印象を持った。あくまで素人がネットで集められるデータの範囲だが。

長々と書いてきたけど、言いたかったことは以下の通り。

去年の12月29日の拙記事 の最後に「多分しばらくはボックス相場だろうな」と書いてしまったが、前言撤回で、今後ビットコインのレートはかなり下がるんじゃないかというのが、簡単な数値モデルに基づく現在の私の予測である。

ということを、きっかけとなったツイートを1月14日に見て以来、書こう書こうと思いながら、なかなか書けずに半月間温めていたら、その間にコインチェック事件が起きたり、インドなどいくつかの国で仮想通貨に対する厳しい規制が実施されたりで、目下、仮想通貨全般のレートが下降局面にある。

参考までに今回も bitFrier さんより、本日14:30現在のレートをお借りしスクショを貼らせていただきます。

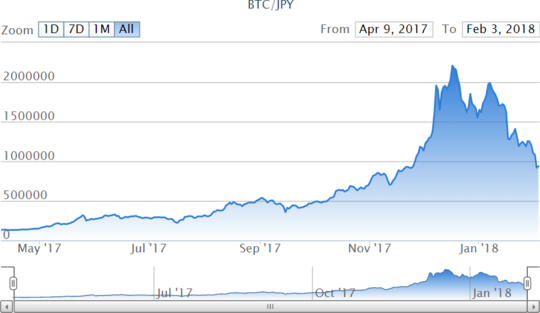
スポンサーリンク