ツイッターに流れてきた問題である。FF 外から引用失礼します。
高校生A「「³√4+2³√10」と「6」どちらが大きいけ?」
— ねこ (@nekonyannyan821) 2020年9月18日
高校生B「んー。とりあえずどちらも3で割る?f(x)=³√xとすれば一方は(4,f(4))と(10,f(10)の2:1内分点のy座標じゃん?他方f(8)だから・・」
高校生A「あーなるほど!」
教員「(さっぱりわかんらん)」
私もさっぱりわからんかった。
FF さんでもある id:Sampo さんの、次のコメントを読んで、ようやくわかった、気がした。
ちなみに私は、ねこ @nekonyannyan821 さんのツイートは Sampo さんのRT経由で読んだ。
3で割ると、「⅓³√4+ ⅔³√10」と「³√8」の比較になります。
— 投機的実行《アクセラレーション・ブースト》 (@yuba) 2020年9月19日
³√xは上に凸の曲線だから、内分点は曲線よりも下に来ると。
Excel でグラフを描いてみた。
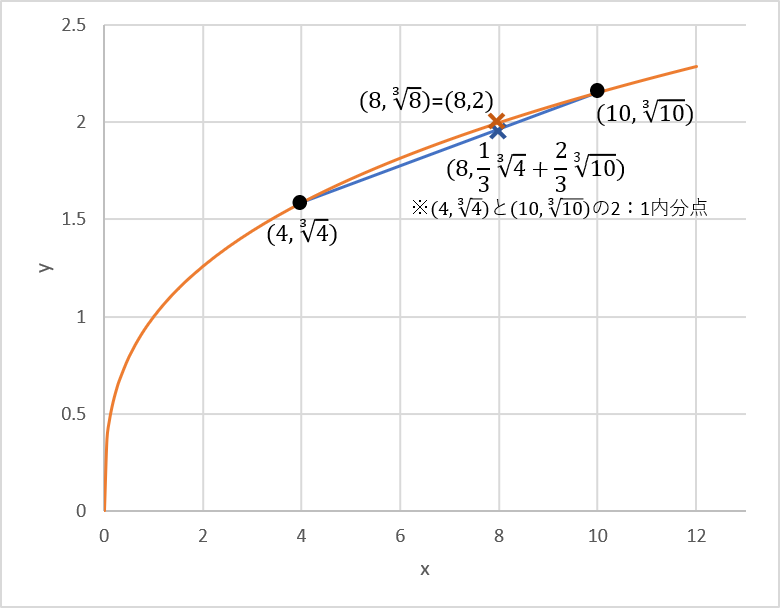
オレンジ色のグラフが y = ³√x である。
グラフ上の2点 (4, ³√4 )、 (10, ³√10 ) を結んだ線分を青色で表す。
青色の線分の x = 8 における点(グラフ上の青い✖)が、高校生 B の言うところの「(4,f(4))と(10,f(10))の2:1内分点」である。
この点の座標が
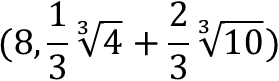
であり、y 座標の値に3を掛けると高校生Aのいう「³√4+2³√10」になるのだ!
そしてオレンジ色のグラフの x = 8 における点(グラフ上のオレンジ色の✖)の座標は
(8, ³√8) = (8, 2)
であり、y 座標の値に3を掛けると6になる。
y = ³√x のグラフは上に凸なので(オレンジ色の✖は青い✖の上にある、すなわち) ³√4+2³√10 < 6 というのが結論である■
念のため数値計算すると ³√4+2³√10 ≒ 5.89627 < 6 である。
改めて ねこ さんの最初のツイートを読み返すと、2~3行目の高校生Bのセリフの中に必要な情報が全部含まれているではないか!
私は Sampo さんのヒントをもらい、自分でグラフを描いて、ようやくわかった。
どうやって思いつくんだろう、こういう問題と、解法。
でも高校生Aや高校生Bのような奴らって、実在するだろうね。
オチをつけるためいらんこと言いの悪癖を発揮すると、高校生Aと高校生Bは進学校に通う男子学生を自然に想像してしまうが、あえてネットロア的なマックで隣の席に座った女子高生で脳内再生してみると(だってそれだけの学力を持った JK は必ずいる)、昨今のジェンダーフリーへの理解を深めるトレーニングになるような気がするし、自分のコンプレックスをさらに自虐的にいたぶることができるようにも思う。
スポンサーリンク