一昨日(4/29)付 に続いての数独(ナンプレ)ネタの連投になるが「番外編」とタイトルするのは去年の10/22付以来、約半年ぶりである。まあ独自研究といったつもりである。
一昨日付のほうに書いたことだが、1つの問題中に同時に2つの井桁が成立するとき、どちらの井桁に着目しても除外できる数字の候補は同じではないかということに気づいたので、それをまとめたい。
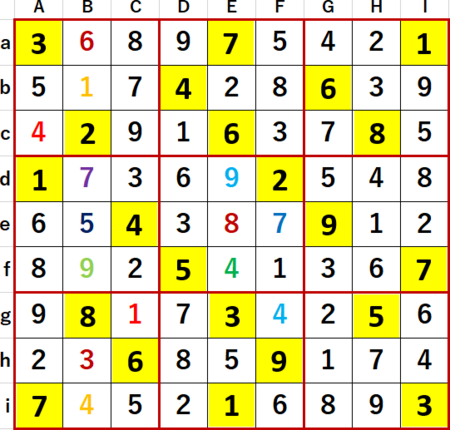
タネ本『超激辛数独1』からページをさかのぼって問題を2題示す。まずはP74の67。難易度はLevel10+、作者は 我ヒトにあらず さん。初期値を背景色黄色で示す。
今回からタネ本Solutionsに倣って、列を表す大文字アルファベットと行を表す小文字アルファベットも付加してみた。これまで「最上行最左列」などと表記してきたがAaと簡潔に表せるからだ。Aaには4が入っている。もっと早くやればよかったと思うが、改めるのに遅すぎることはないとも言うので。
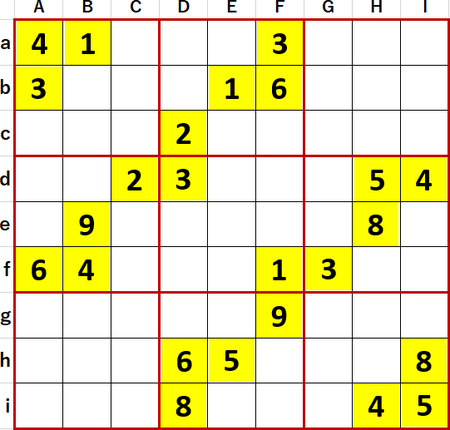
確定できる数字は確定し、確定できないマスには候補の数字のメモを書き尽くした状態が下図。
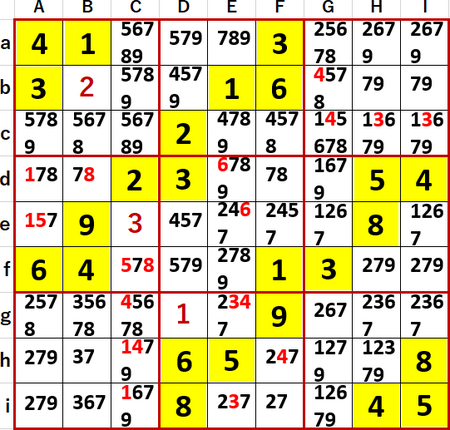
P118のヒントには
(abf・CDG)…5井桁
(abf・CEG)…8井桁
と書いてあった。でもヒントは見ないで解いたよ、といらんことをつけ加えてみる。
まずはヒントの1行目から見ていく。5が飛車にらみを利かせるマスを灰色で、(abf・CDG)…5井桁を構成する空白マスを濃いオレンジで(3連井桁だ!)、それ以外の5を候補に含むマスを薄いオレンジで着色する。
井桁理論について簡略におさらいしつつ、除外できる候補を確認する。
この図の場合a行、b行、f行の3行において、5が入るのはC列、D列、G列の3列に限定される。
もしa、b、f以外の行のC列かD列かG列に5を入れたら、a、b、f行では5が入る空白マスが足りなくなる。
よってa、b、f行以外のC、D、G列の候補から5を除去することができる。この問題の場合、具体的には空白マスcC、cG、eD、gCに入る数字の候補から5を除去することができた。上図中ではフォント色を灰色に変えて示している。
もう一言、この作業を「行方向に着目して井桁を見つけ、列方向の候補を除いた」と形容してみる。
ところが同じ問題の同じ状況においては、(ceg・ABF)…5という3連井桁を見つけ出すこともできるのだ!
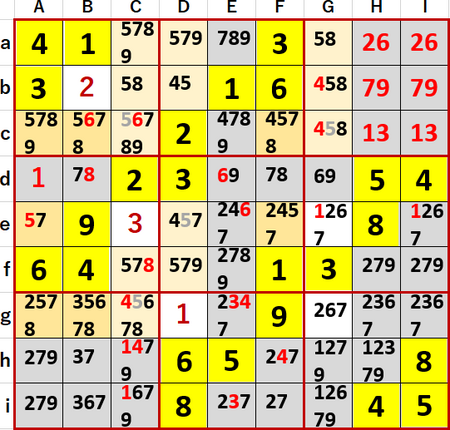
この場合A列、B列、F列の3列において、5が入るのはc行、e行、g行の3列に限定される。
もしA、B、F以外の列のc行かe行かf行に5を入れたら、A、B、F列では5が入る空白マスが足りなくなる。
よってA、B、F以外の列以外のc、e、g行の候補から5を除去することができる。具体的には空白マスcC、cG、eD、gCに入る数字の候補から5を除去することができた。上図中ではフォント色を灰色に変えて示している。
またこの作業は「列方向に着目して井桁を見つけ、行方向の候補を除いた」と形容してみる。
さっきの「行方向に着目して井桁を見つけ、列方向の候補を除いた」場合と、除けた候補が完全に一致しているではないか!
ちなみに私がどっちを使って解いたかは忘れた。
一例だけなら偶然かも知れないけど、問題を解いていると同様の現象が次々と現れる。
同じ問題をもう少し進行させてみる。
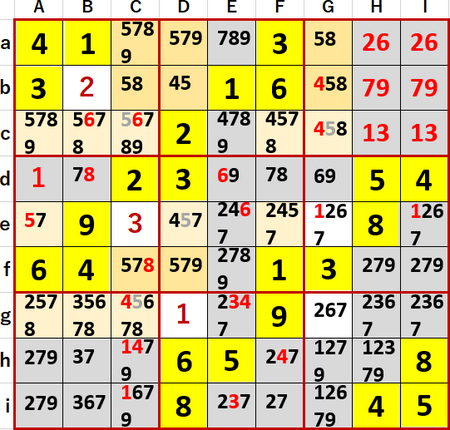
ヒント2行目「(abf・CEG)…8井桁」なのだが、先般と同じ着色(8の飛車にらみ:灰、ヒントの8井桁:濃い橙、それ以外の8の候補:薄い橙)を行ったのが次図である。
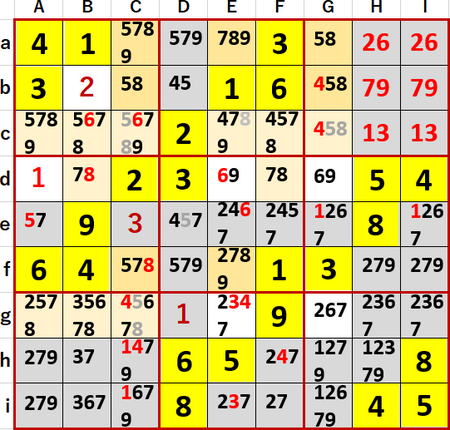
これは「行方向に着目して井桁を見つけ、列方向の候補を除いた」作業であり、結果として空白マスcC、cE、cG、gCに入る候補から8を除去することができた(フォント色灰色で表示)。
前図と同じ状況において、「列方向に着目して井桁を見つけ、行方向の候補を除」く作業をやってみると、(cdg・ABF)…8井桁というのが見つかった!
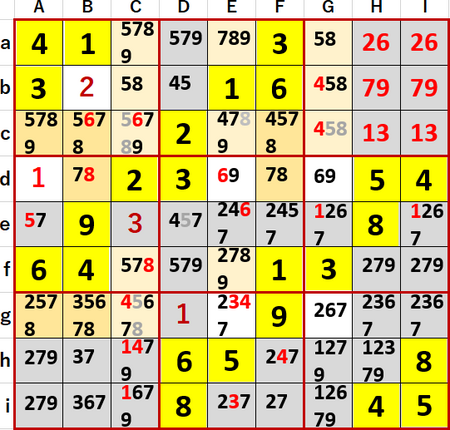
この結果、除去できる候補はcC、cE、cG、gCの8で、一つ前の図の場合と全く同じである。
ここでもどっちを使ったかは覚えていない。人間の思考にはクセがあるから、どっちかに偏っている可能性が高いと想像するのだが。
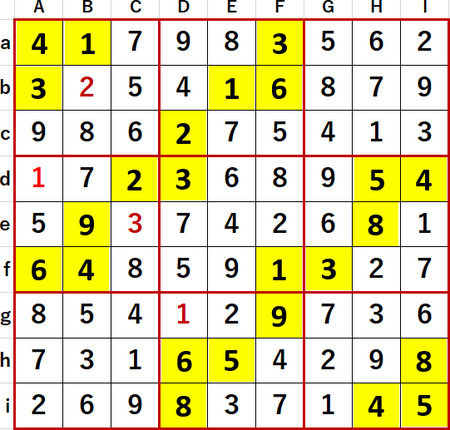
結論としてはセルcGに4が確定したことをきっかけに多重選択の連鎖的解消が始まり、次図のような最終形を得ることができた。Solutions P118と一致している。
もう1問、解いてみる。68、70は「予約」解法が大きな役割を果たすのでスキップしてP76の69を。難易度はLevel10+、作者は 鴈野敏生 さん。初期値を背景色黄色で示す。
確定できる数字を確定し、確定できないマスには候補の数字メモを書き尽くした状態。
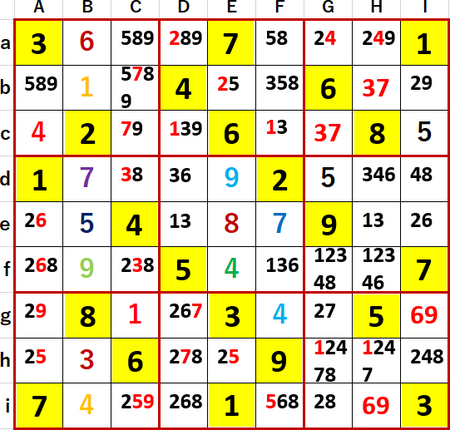
Solutions P119のヒントには
Ab・Ah・Eb・Eh…5井桁
Ib・Ie・Ig…2・6・9予約
Ab・Ag・Ib・Ig…9井桁
と書いてあった。
ヒント1行目を図示するため、5の飛車にらみ:灰、5井桁:濃い橙、それ以外の5の候補:薄い橙で着色した。今回は単純井桁、X-Wingだ。
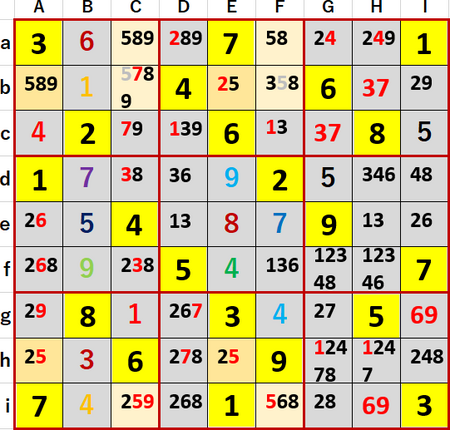
これにより空白マスCb、Fbの候補から5を除外することができた。
列方向に着目して井桁を見つけ、行方向の候補を除く作業だった。
同じ5について、行方向に着目して井桁を見つけ、列方向の候補を除く作業をやってみる。
Ca・Ci・Fa・Fiというのが見つかった。
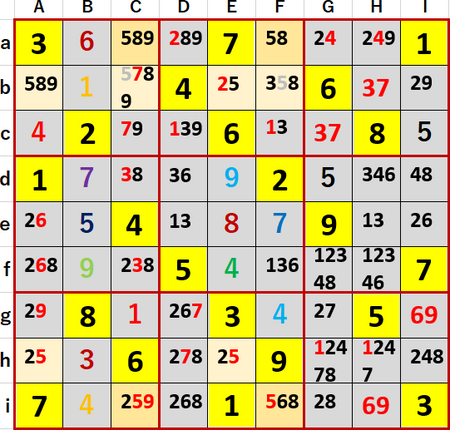
これにより候補から5を除外することができる空白マスはCb、Fbで、一つ上の図の場合と同じだった。
実は私は、ヒント2行目の「Ib・Ie・Ig…2・6・9予約」と3行目「Ab・Ag・Ib・Ig…9井桁」を使わないで、代わりに(beh・AEI…2井桁)というのを用いて解いた。3連井桁、メカジキ法である。
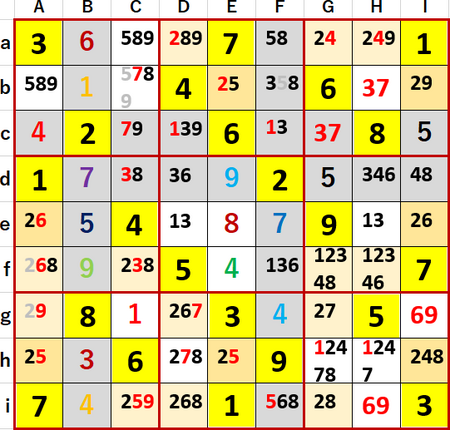
この結果Af、Agの空白マスに入る候補から2を除外でき、特にAgに9が確定したことをきっかけに、多重選択の連鎖的解消を開始させることができた。
これは行方向に着目し列方向の候補を除外する作業だったが、列方向に着目し行方向の候補を除外する作業も、あえてやってみた。
(afgi・CDGH…2井桁)というのを見つけた。4連井桁、ゼリーフィッシュ法である。
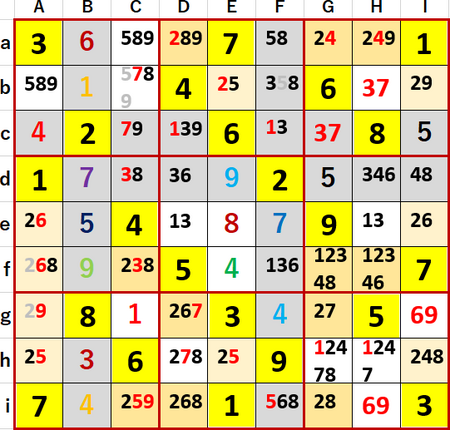
この結果でもAf、Agの空白マスに入る候補から2を除外できたことは、これまでと同様である。
Agに9が確定したことをきっかけに導出した最終形を示す。ヒントとやり方が違ってもSolution P119と一致していることには変わりない。
他にも何問か当たっているが、1つの問題中に同時に2つの井桁が成立するとき、どちらの井桁に着目しても除外できる数字の候補は同じという経験則の例外には、未だ遭遇していない。
この法則に、名前を付けたい。「井桁ケンカせずの法則」なんてどうでしょうか?
またこの法則は、何らかの形で証明ができるんじゃないだろうかという気がする。
まだ固まったわけではないが温めているアイデアないわけではない。いずれ続編を書くつもりで、ブログタイトルに「その1」と入れてみた。