考えがまとまっていませんが、速報的に。
前回のエントリーには、1日で1万9千超のpvをいただき、感謝しています。ありがとうございました。

また何名もの方からブログにて言及をいただきました。こちらも感謝しつつ、失礼してリンクを貼らせていただきます(公開順)。
コメント欄やブックマークコメント欄にも、いくつかの興味深いご指摘をいただきました。感謝します。
すみません、量が多くて確認が追いつきませんが、少しずつ読ませていただいています。
とりわけ前回のエントリーでは「自明解」としてゾロ目(111、222、333…)のみを挙げましたが、何人かの人からご指摘をいただいた通り、キリ番(100、200、300…)も自明解(計算結果は0)であることに言及しておくべきでした。今回の趣旨にも関係がありますので、先に一言しておきます。
冒頭でも述べた通り、今回は速報的なエントリーです。
この手の数論めいた問題に共通するやっかいさと面白さは、データの上限にキリがないことだと思います。
今回の問題の場合、3桁という縛りを外してもゾロ目やキリ番の自明解は存在します。
4桁の場合、自明解は、1000、2000、3000…、1111、2222、3333…です。非自明解を、今回も力づくで計算してみます。
前回のExcelシートをちょっと改造して、2桁目と3桁目の数字として00~99の100通りのデータを入力する手間を惜しまなければ、簡単に調べることができました。
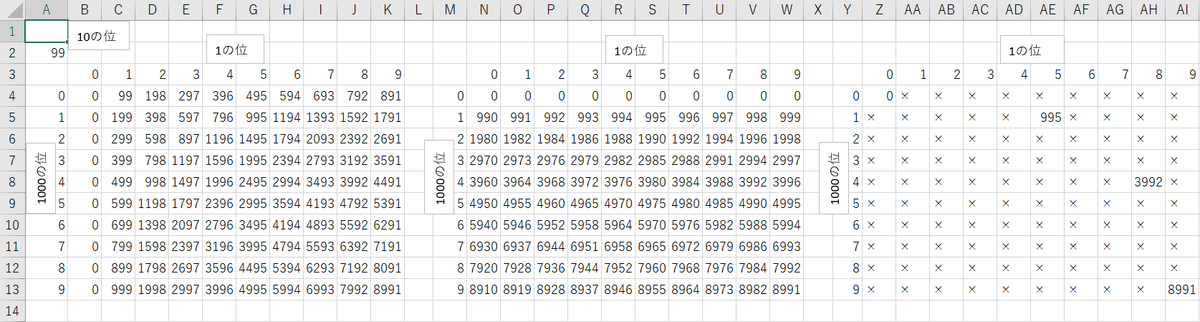
前回との違いは、セルN4の数式 "=(10*$A4+$A$2)*B$3" を "=(100*$A4+$A$2)*B$3" に変更してセルW13までコピーするだけでした。
あとはセルA2に0~99の100通りの数字を入力すればよかったのです。
結果として、見落としがなければ次の6通りの非自明解が見つかりました!
1664 166×4=1×664= 664
1995 199×5=1×995= 995
2665 266×5=2×665=1330
4847 484×7=4×847=3388
4998 499×8=4×998=3992
7424 742×4=7×424=2968
追記:
b:id:asedaruma さんからブコメで
6545 654×5=6×545=3270
の漏れをご指摘いただきました。ありがとうございました。
また何人かの方からブコメやトラックバックで
164、1664、16664…
195、1995、19995…
265、2665、26665…
498、4998、49998…
が無限桁で条件を満たすこともご指摘いただきました。ありがとうございました。
追記おわり
追記の追記:
3桁の4つの非自明解は、すべてこのタイプ!
追記の追記おわり
それでは5桁以上の場合はどうなるでしょうか? Excelでは面倒ですが、プログラムを書いて計算時間を惜しまなければ、しらみつぶしの計算はそれこそ無限桁まで容易に可能でしょう。制限はコンピュータの能力のみです。
しかし、それを解析的に求めることはできるのか? 非自明解は無限桁まで存在するのか? 分布はどうなっているのか?…等々の問題は、数論的にちょっと面白い問題になるのではないかという予感がします。
ですが前回のエントリーでも書いた通り、私の手に遥かに余るという予感もあります。無責任にも問題として投げっぱなしにしておきます。
スポンサーリンク