自己満足的数独(ナンプレ)のプレイ記録である。前回はこちら。
タネ本ニコリ『超激辛数独4』終盤に至って難問目白押しである。むしろウェルカムそう来なくっちゃ。
難度が上がるということは、最も単純な数値化としては2大解法「n連井桁」と「n国同盟」のnの数が増大することだ。しかし、いずれもnには4という上限がある。行方向にn連井桁が成立していれば、列方向には同時に最大9-n連井桁が成立する。行または列または3✕3ブロック中にn国同盟が成立していれば、同時に最大隠れ9-n国同盟が成立する。よって、いずれも5より小さい数字が必ず現れるというわけだ。
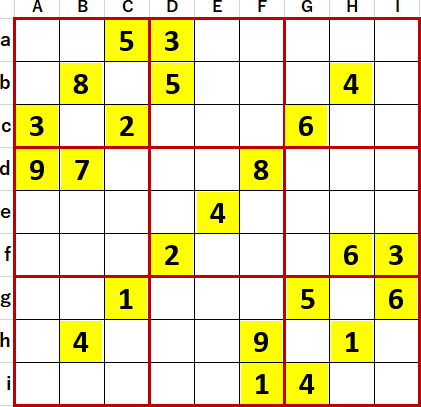
だからと言って、4国同盟が出現する問題の難度が最も高いとは言い切れない。少し前に解いた問題だが『超激辛数独4』P71 64。作者 G さん。難易度Level10+。初期値を背景色黄色で示す。
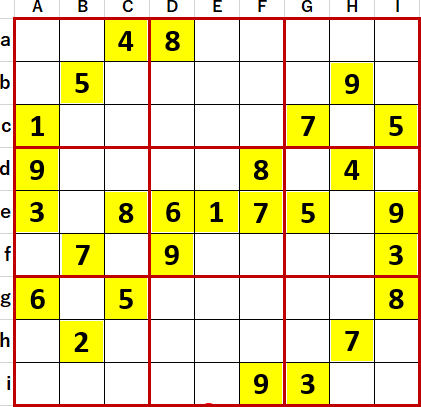
初等解法で埋められるマスを埋め、埋められないマスには候補として入りうる数字のメモを書き尽くした状態のスクリーンショットが次図。
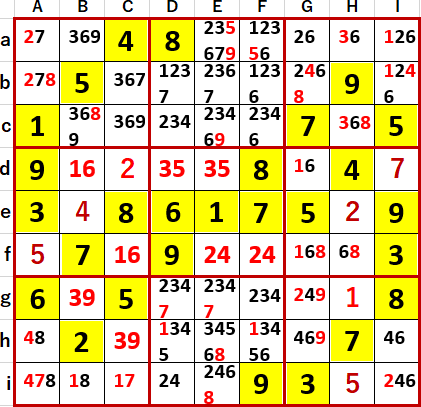
下段中央3×3ブロック中に2・3・4・7 4国同盟(1・5・6・8 隠れ4国同盟)を見つけた。
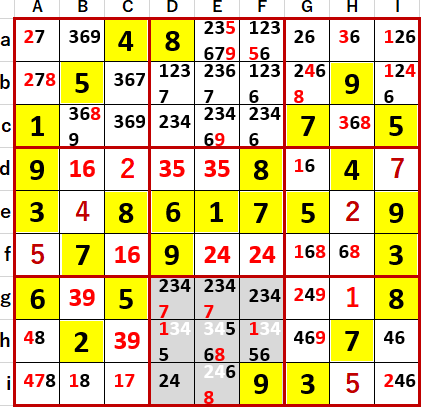
これによりBgに3、GgとChに9が確定し、これらをきっかけに、あっさり多重選択の連続的解消が始まった。
得られた最終形を示す。Solutions P117と一致している。
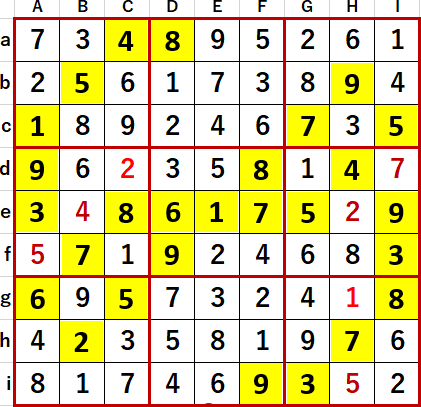
同ページのHintには
Bg・Ch…3・9予約
1…Bi・Ci→Dh・Eh・Ei・Fb…1・5・6・8予約
と書いてあった。1行目は2枚目(2枚上)のスクショに反映済み、2行目前半はニコリさん呼称「いずれにしても理論」のヒントにおける記述で、下段中央3×3ブロックのi行の候補から1が除外されるという意味だと思われる。
手こずったのが、直近で解いたP78 71。先に書いてしまうが、3国同盟ないし隠れ3国同盟以上の難度の解法は使わなかった、にもかかわらずである。作者 高由良りむ さん。難易度Level10+。初期値を背景色黄色で示す。
埋められるマスを埋め、埋められないマスには候補として入りうる数字のメモを書き尽くしたのが、次のスクショ。この状態を導くのに3および5の井桁を使用したが、省略する。
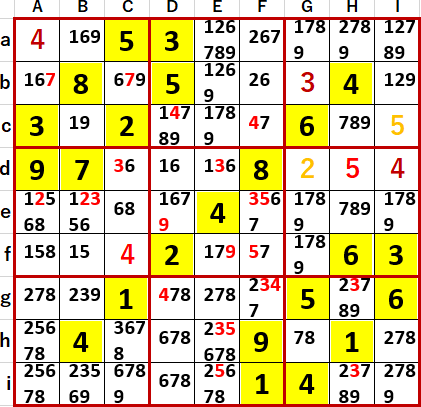
中段行方向に1のローカル呼称「2の2の3」が見つかった。これにより中段中央3×3ブロックDeとEfの候補から1を除外することができた。
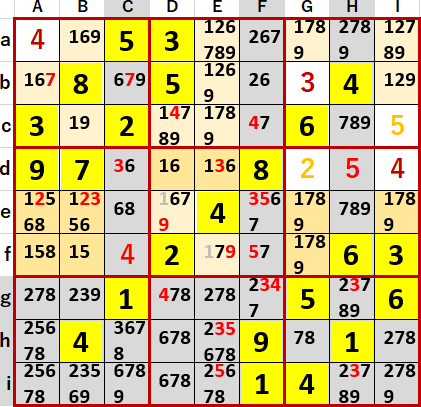
これを受けてe行に2・3・5 隠れ3国同盟(1・7・8・9 4国同盟)が発覚した。n国同盟は同盟を構成するマス以外の候補から同盟を構成する数字を除外し、隠れn国同盟は同盟を構成するマスの候補から同盟を構成する数字以外を除外する。
中央3×3ブロック2の2の3によりEaとEbの候補から6が除外できた。
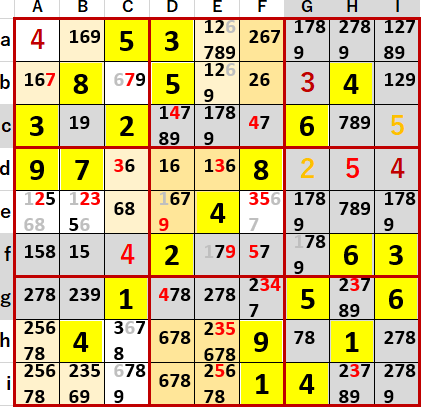
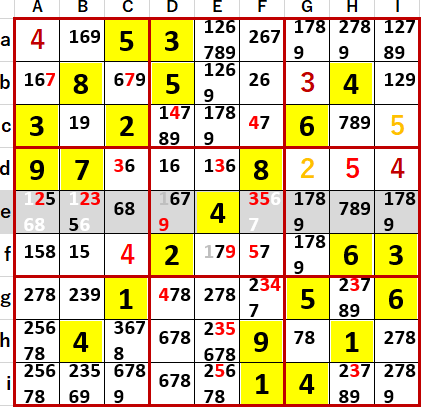
これでE列に3・5・6 隠れ3国同盟が発覚した。
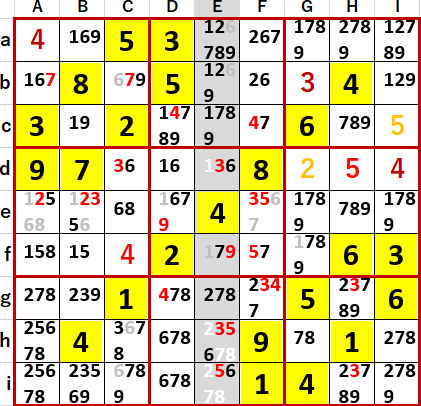
下段中央3×3ブロックDhとDi 6のいずれにしても理論により、Ddに1が確定した。だがまだ多重選択の連続的解消には至らなかった。
多重選択の連続的解消に至ったのは、同じく下段中央3×3ブロックだがEgとFgの2いずれにしても理論を適用することにより、下段左側3×3ブロックに2・5・6 隠れ3国同盟が発覚した。あとから振り返ると、これを見つけるのが一番苦労した。
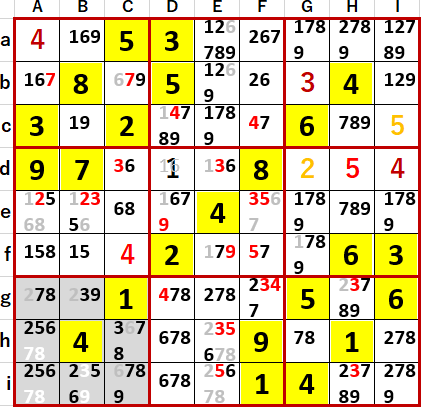
2・5・6 隠れ3国同盟は、A列とi行にも適用できることがわかった。
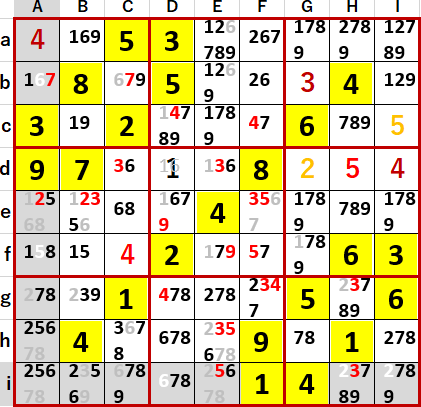
Abに6、Ihに2が確定したことをきっかけに、ようやく多重選択の連続的解消が始まった。
得られた最終形を示す。Solutions P119と一致している。
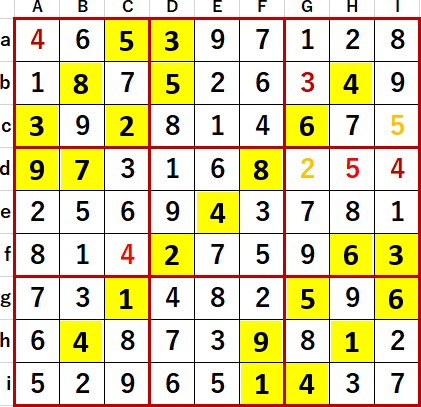
同ページHintには
5…Eh・Ei→Hd…5
Cd・Ed・Ch・Eh…3井桁
Ae・Be・Fe…2・3・5予約
Ed・Eh・Ei…3・5・6予約
Ah・Ai・Bi…2・5・6予約
Ae・Ah・Ai…2・5・6予約
と書いてあった。1行目&2行目は、省略した部分にあった。3行目は8枚目6枚上、4行目は10枚目4枚上、5行目は11枚目3枚上、最終行の6行目は12枚目2枚上のスクショに対応している。今さらながら、図番をつけときゃよかった。
今回は(も?)タイトルに偽りありで、単純にn国同盟や隠れn国同盟のnが大きいことより、最終形を導くまでに必要な手数が多ければ多いほど困難を感じることを結論にしたほうがよさそうである。
ただし4国同盟や隠れ4国同盟を、この71ほど何段も仕込んだ問題が作れるかどうかは、問題を作った経験のない私にはわからない。
弊ブログはアフィリエイト広告を利用しています
