すみません、今回はお詫びからです。8月19日付拙過去記事(現在公開停止中)でニコリ『超激辛数独2』P55 48について「別解のある問題ではないか?」と書いてしまったのですが…
私が解く過程および最終形として得られた図として示した画像に対して、ブックマークコメントにて「AaとAeに2が、CbとCiに6が重複している」というご指摘を頂きました。ありがとうございました。
あああ、これは言い訳のしようがないミスです。大変失礼しました。作者の ちばけいすけ さんにも、お詫び申し上げます。ごめんなさい。
改めて解いてみた最終形です。Solutions P113および同ページのヒントとも矛盾はありませんでした。
数独(ナンプレ)を解くにあたっての最大の敵は自分自身のミスだと、拙過去記事で何度となく繰り返しています。弊ブログにアップロードしなかったものの「解けた」と思った問題の中にも、ミスを犯してそれに気づかぬまま「解けた」と思い込んでいる問題が何問もあるかも知れません。
8月19日拙記事は自己検証の結果、公開する意義が見当たらないと判断し前述の通り非公開にしました。そうするとLevel10+に突入して以後の記事がなくなるため、その後に解いた問題のうち難度が高いと感じたものを2問ほどアップします。いずれも1度で解けず、2晩以上寝かして最終形にたどり着いた問題です。
サムネイルは いらすとや さんからお借りします。

https://www.irasutoya.com/2015/11/blog-post_117.html より
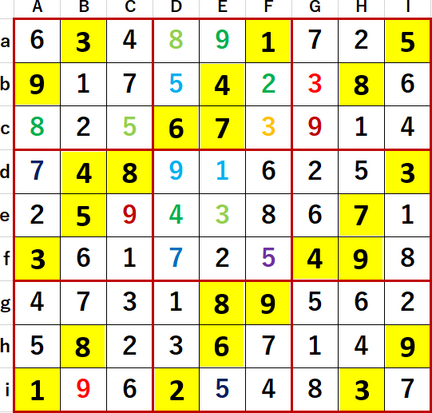
まずは『超激辛数独2』のP63 56。難易度Level10+、作者 高由良りむ さん。初期値を背景色黄色で示す。

ローカル呼称「2択先書き法・改」にて初等的に埋められるマスは埋め、埋められないマスには候補の数字を書き尽くしたのが次図。ローカル呼称「井桁塗り分け法」による井形のチェックも並行して行ったが、井桁は見つけられなかった。

少し時間がかかったがローカル呼称「2の2の3」解法により最初の手がかりを見つけた。

下段3行の7に着目すると、中央と右側の3×3ブロックにはh行とi行にしか存在しない。もし左側の3×3ブロックでh行かi行に7を入れると、中央と右側の3×3ブロックのどちらかには必ず7を入れられない行が出現する。よって下段左側3×3ブロックの7はg行に入り、同ブロックh行とi行の空白マスの候補から7を除外することができる。
これによりChに3が、Ciに9が確定する。またCdの9の2択の片割れが消えるので、残りの9がAdに確定する。
しかしこれだけでは、多重選択の連鎖的解消は導けなかった。
決定打は、上段左側3×3ブロックで2・4・5・7の4国同盟ないし1・3・8・9の隠れ4国同盟を見つけたことだった

行または列または3×3ブロックにおいて確定マスがM個ありN国同盟が成立すれば、同時に隠れ9-M-N国同盟が成立する。
よって最も難しいのは…
M=0の時の4国同盟と隠れ5国同盟、5国同盟と隠れ4国同盟
M=1の時の4国同盟と隠れ4国同盟
である。
つまり4国同盟ないし隠れ4国同盟を見つけることは、このパターンの解法テクニックでは難易度最高と言えよう。
これまでの経験上、3国同盟or隠れ3国同盟はなんとか見つけられるようになったが、4国同盟or隠れ4国同盟を見つけるのは、場数を踏んでいないためまだまだ困難を感じる。
ともあれこの結果、上段左側3×3ブロック中で4がc行にしか残らなかったためHcに8が、Icに5が確定し、ようやく多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P115と一致している。

同ページのヒントには
7…Ag・Bg→Ch…3
Aa・Ab・Ba・Bb…1・3・8・9予約
と書いてあった。
1行目は3枚上の図の「2の2の3」のことだと思う。
2行目は2枚上の図に対応する。「予約」は「N国同盟」「隠れN国同盟」に対応するニコリさんの呼称である。
続いて『超激辛数独2』P66 59。難易度Level10+、作者 我ヒトにあらず さん。初期値を背景色黄色で示す。

初期値と候補を埋めていく過程で「井桁塗り分け法」により見つけられた井桁は、4のBa・Bg・Ha・Hg列方向単純(AGI・bfh行方向3連)だけだった。

初等解法により決定できるマスは決定し、決定できないマスには入る数字の候補メモを書き尽くした状態が、次図。

この問題の特徴は、初期値に7が存在せず、全ての未確定マスの候補に7が残ったことだった。
初期値に特定の数字が存在しない問題はよくあるが、「一気通貫」「総消去法」「いずれにしても理論」といった初等解法でその数字が確定できたことがほとんどで、この問題のように全ての未確定マスにそれが残ることは珍しい。
それが原因で、苦戦を感じた。
まず見つけた手掛かりは、「2の2の3」解法により下段左側3×3ブロックからC列以外の5の候補を除けることだった。

5の何度目かの井桁塗り分け法チェックをやっているときに見つけたので、スクショに塗り分けが残っています。残した方がわかりやすいかなと思って残した。
(なお後でヒントを参照したところ、C列の2・5予約で同様の結果を得ていた。あっ、なるほど)
この結果を踏まえてi行に2・5・9隠れ3国同盟ないし1・3・7・8 4国同盟が見つかった。

F列に「一気通貫」を適用することにより、Fbの1が確定した。
この1が3の2択の片割れを消すことにより、Fcの3が確定した。
だが、まだ多重選択の連鎖的解消には至らなかった。
もう一度、井桁をチェック。Ba・Bi・Ha・Hiに3の列方向単純井桁(ACI・bdh行方向3連井桁)が見つかった

この結果を受けて、a行に3・4隠れ2国同盟が見つかった。

H列の「一気通貫」によりHeに1が確定し、これでようやく多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P116と一致している。

同ページのヒントには
Cg・Ci…2・5予約
Ci・Ei・Fi…2・5・9予約
Ba・Bi・Ha・Hi…3井桁
Ba・Bg・Ha・Hg…4井桁
Ba・Ha…3・4予約
と書いてあった。下から2行目の4井桁を私は1行目の2・5予約に先立って見つけたが、結果に影響を与えないのだろう。
スポンサーリンク