自己満足的数独(ナンプレ)のプレイ記録である。前回はこちら。
タネ本であるニコリ『激辛数独』シリーズ(と言っても1と2のまだ途中までしかやってないが)の2大解法は「井桁」と「予約(N国同盟)」であるが、直前拙記事の何回かには「井桁より予約の方が個人的には苦手だ」と書いてきた。
その理由について、井桁についてはローカル呼称「井桁塗り分け法」というのを開発した旨も、何度となく述べてきた。
しかし井桁も舐めてはいけない。『超激辛数独2』のP69 62で、またも未知のパターンに対面した。難易度Level10+、作者 Gemini さん。初期値を背景色黄色で示す。
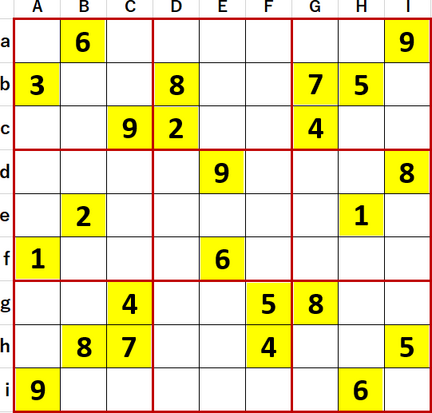
まずはローカル呼称「2択先書き法・改」にて初等解法で埋められる空白マスは埋め、埋められないマスは候補として入りうる数字で埋め尽くすことを試みる。その過程で井桁塗り分け法も同時進行的に適用している。
次図は6について、井桁塗り分け法を適用しているところ。
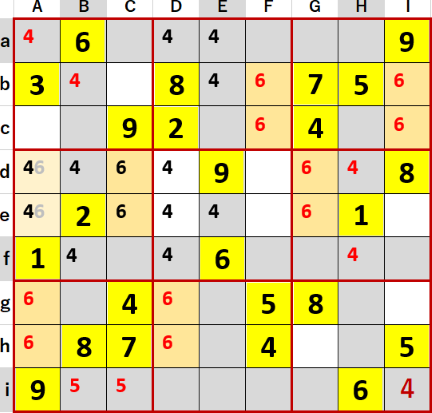
上図では6の初期値が飛車にらみを利かせるマスを灰色で、井桁を構成するマスを濃い目の橙で、井桁が候補の数字から6を除外するマスを薄い橙で着色している。
6についてはAg・Dg・Ah・Dhに行方向単純井桁、Cd・Gd・Ce・Geに列方向単純井桁が見つかった。これによりAdとAeの候補から6を除外できた。
なおFb・Ib・Fc・Icには独立単純井桁が存在している。すなわち1度に3つの井桁が併存している状態である。
そんなで1~9までのすべての数字につき、初等的に埋められるマスは埋め、埋められないマスには候補の数字を書き尽くした。埋めたマスについては埋めた順にExcelカラーパレットの左からフォント色を与えている。3×3ブロックで候補が2択になる数字については、フォント色赤を与えている。
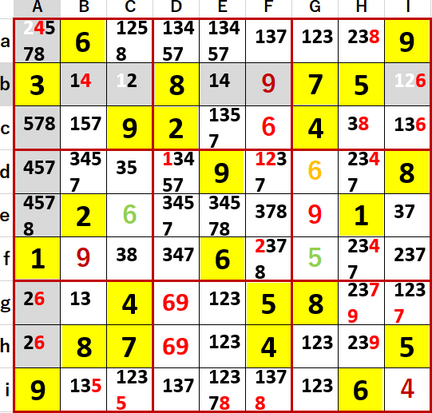
b行Bb・Ebの1・4 2国同盟、A列Ag・Ahの2・6 2国同盟はすぐに見つかったので、それぞれの2国同盟により決定したマスを埋めた次図が、実質スタートだった。
というより、この状態から進展がなく、何晩か寝かせた。
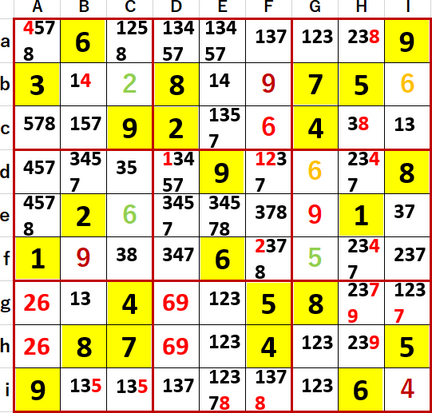
前回9月1日付記事 で述べた単純ミスを最終形だと思い込んでいた問題は「勝敗」で言うとしたら間違いなく「負け」だが、『超激辛数独1』を解いていたときの拙過去記事には「Hintを見ることを敗北と定義する」と何度か書いていた。
『超激辛数独2』に入ってからは、まだ解けずにヒントを見た問題はなかった。
そろそろ「負け」を覚悟しなきゃならないかなと思いながら、何巡目かの井桁の再チェックを行ったとき、1について井桁が成立するのをずっと見逃がしていたことに、やっと気づいた。
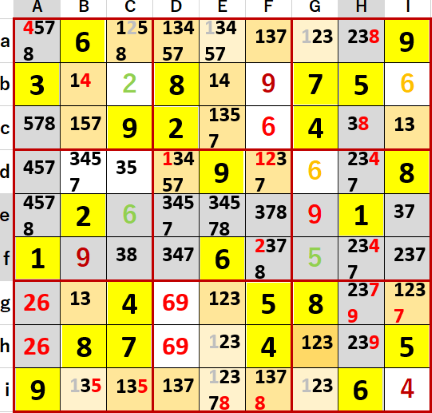
すなわち(CDF・adi)の列方向および(BEI・bcg)行方向3連井桁であるのだが、そしてそれらの井桁により薄い橙で着色したマスに入る候補から1が除外されるのだが、しかし両井桁の干渉を受けない単独のマスGh(より濃い橙で着色)が残っているではないか!
こんなケースは初体験だ! こういう事態を、どう認識したらいいのだろう?
愚考は後述するとして、いくつかのマスの候補から1が消えた結果を整理してみた。
G列のローカル呼称「一気通貫」により、Ghに1が確定した。
上段右側3×3ブロックではIcのみに1の候補が残るので、同マスに1が確定した。
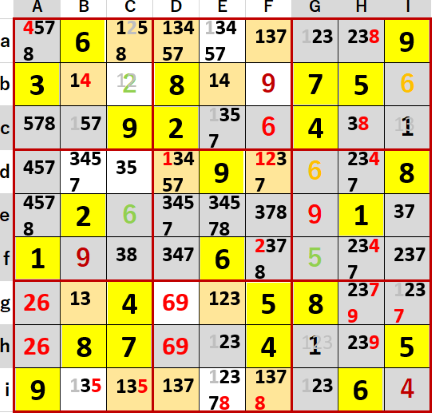
これらを受けて1について整理し直すと、(CDF・adi)の列方向3連井桁とBb・Eb・Bg・Egの行方向単純井桁が残った。
結論を急ごう。3について井桁の再チェックを行ったところ、Ec・Hc・Eh・Hhの行方向単純井桁が見つかった。
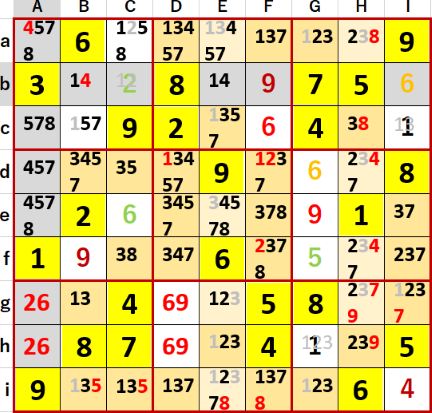
中段右側3×3ブロックで3が候補に残るのはI列のIeとIfのみ。
「いずれにしても理論」によりIgの候補から3が消えるので、g行では一気通貫によりBgに3が確定した。
この3を手がかりに、多重選択の連鎖的解消が始まった。
得られた最終形を示す。Solutions P117と一致している。
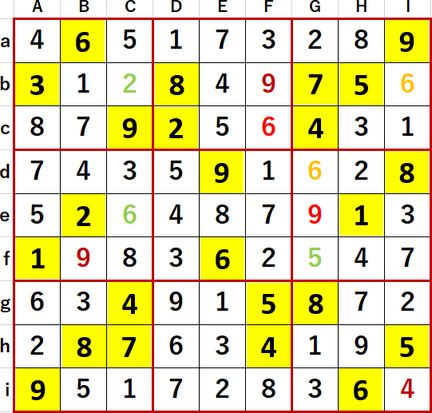
同ページのヒントには
(BEI・bcg)…1井桁
Ec・Hc・Eh・Hh…3井桁
Ac・Ae・Ec・Ee…5井桁
と書いてあった。
上2行は確かに使ったが、5の井桁は使ったっけ?
まあいい、この問題での個人的なもっぱらの関心事は、5枚目(4枚上)の図で、行方向の井桁からも列方向の井桁からも干渉を受けないマスGhが1つだけ残ったことを、どう解釈するかだ。
2枚目の図で6の井桁をチェックしたとき、行方向井桁とも列方向井桁とも重ならない独立井桁が見つかったことを書いた。独立井桁は過去記事に何度か出てきた。
過去の独立井桁はすべて2マス×2マスだった。3マス×3マス以上の独立井桁も存在する可能性はあるが、まだお目にかかったことはない。
他の井桁の干渉を受けない単独のマスは、1×1の仮想的な井桁と考えるのが、もっもらしく感じられる。仮想的と言ったのは、未確定候補は同一行or列or3×3ブロック中の複数マスに存在しないと生き残れない=確定してしまうからだ。確定してくれた方がありがたいのだけど。そもそも全てのマスを確定することが、数独というパズルの目的なのだけど。
現に今回のGhにも1がただちに確定した。
今後もし同様のケースに出くわしたら「1×1仮想井桁」とローカル呼称することにしよう。
1×1仮想井桁は出てきたら即確定と考えてよさそうな気がするが、未検証である。
突飛な喩えを思いついた。他人に通じにくそうな喩えを思いつくことにはメリット少ないし私の数多い悪癖の一つと言っていいが、記憶に残すために。
何十年も昔、『ホーキング、宇宙を語る』という本を読んだことがある。
故ホーキング博士の「ブラックホール消滅理論」を一般読者向けにわかりやすく解説した書だった。
うろ覚えだが同書によると、不確定性原理により真空中では粒子と仮想粒子(反粒子)の対生成と対消滅が常に繰り返されているという。
ブラックホールの表面でも、この現象は行われている。
このときもし粒子がブラックホールに吸収されると、仮想粒子は単独では安定的に存在できない。
もし仮想粒子がブラックホールに吸収されると、粒子のみが外部に放出される。これが「ホーキング放射」と呼ばれる現象であり、この現象の結果ブラックホールはものすごく長い時間をかけてではあるが徐々に質量を失い、やがて「蒸発」するという。
どこが合っているかというと、「1×1仮想井桁は単独では存在できない」というところだけだが…

