自己満足的数独(ナンプレ)のプレイ記録である。前回はこちら。
上掲記事では最終形を導く決定打となる井桁を見つけるのに苦労し、その理由として井桁の干渉を受けない単独マスが存在した旨を述べた。井桁の干渉を受けない単独マスについては、戯れに「1×1仮想井桁」というローカル名称を与えた。仮想というのは「安定して存在できない」という意味である。
だけど1×1仮想井桁は、以前にも見た記憶があった。しかし過去問を解いたExcelファイルは残してあるのだが、サルベージはできなかった。探す手がかりがないのだ。
だがその後すぐ1×1仮想井桁が出現した問題に出くわした。案外ありふれた現象なのかも知れない。
タネ本ニコリ『超激辛数独2』P77 70。難易度Level10+、作者は ぷろちゃん さん。初期値を背景色黄色で示す。
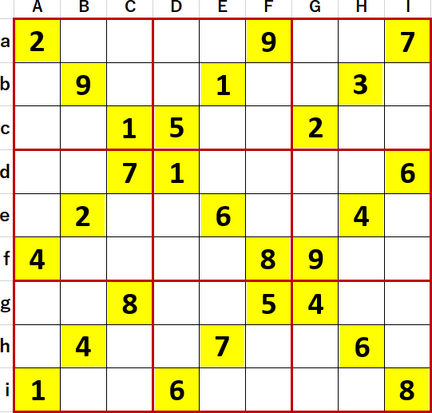
「2択先書き法・改」にて初等解法で埋められる空白マスは埋め、埋められないマスは候補として入りうる数字で埋め尽くそうとしているところ。その過程で井桁塗り分け法も同時進行的に適用している。
次図は8のチェックを行っているところ。

Ab・Gb・Ac・Ge に行方向単純井桁、(BEH・acd) に列方向3連井桁が見つかった。これにより Ac、Ad、Ga、Gd の候補から8を除外できた。
8が飛車にらみを利かすマスを灰色で、井桁を構成するマスを濃いめの橙で、井桁が候補から8を除外するマスを薄めの橙で着色している。
これは、ありきたりの井桁操作である。
次図は4の井桁チェックを行っているところ。

Ed・Fd・Ei・Fi に行方向単純井桁、Ca・Cb・Da・DB に列方向単純井桁が見つかった。これらの井桁に濃いめの橙で、井桁が候補から4を除外するマスに薄い目の橙で着色している。
より濃い橙で着色したIcは、両井桁から干渉を受けない単独マスすなわち1×1仮想井桁である。
このマスは4が即確定でいいと考える。
こうしたチェックを1~9すべての数字に対して行い、埋められるマスは埋め、埋められないマスには候補の数字のメモを書き尽くしたのが、次図である。

Ea・Ec の 3・8 2国同盟および Gd・Gh の 3・5 2国同盟は、比較的容易に見つかった。

この結果を受け、g行に 1・2・3・9 4国同盟ないし 6・7 隠れ2国同盟が見つかった。

この状態から再び井桁チェックを行ったところ、Df・If・Dg・Ig に 3 の行方向井桁が見つかった。

これで多重選択の連続的解消が始まった。
得られた最終形を示す。Solutions P119 と一致している。

同ページのヒントには…
4…Da・Db→Ic…4
Db・Fb・Fc…2・6・7予約
Ab・Gb・Ac・Ge…8井桁
Gd・Gh…3・5予約
Df・If・Dg・Ig…3井桁
と書いてあった。
1行目は3枚目(6枚上)の図に、
2行目と4行目は5枚目(4枚上)の図に、
3行目は2枚目(7枚上)の図に、
5行目は7枚目(2枚上)の図に、
それぞれ対応していると思われる。
