自己満足的数独(ナンプレ)のプレイ記録である。タネ本ニコリ『超激辛数独1』を前回、前々回で終了して、同『超激辛数独2』に突入した。
どうでもいいことだが、これら2エントリーは当初1エントリーにまとめるつもりだった。だから『さらば宇宙戦艦ヤマト 愛の戦士たち』のAmazon画像をサムネに選んだのだが、「さらば」と「対ラスボス総力戦」が揃ってないと必然性弱かったかなと思わないでもない。「さらば」しか合ってないのだったら『さらばシベリア鉄道』でもよかったじゃないか、とか。古い話ばっかりだな。えーっと、えーっと、さらば青春の光! なんの関係があるのだ?
ともかく以前に述べた通りニコリさんの問題集には「超激辛」以上のランクはないのだから『超激辛数独2』しかないとアマポチしたのだが、難易度Level9、9+、10、10+のうちのLevel9に戻るのはなんだかなと思わないでもなかった。波動砲一発、スペシウム光線一閃、ライダーキック一蹴で解ける問題が続きそうな気がしたので。
実際P8 1、P9 2はそんなイメージに近かった。1は「井桁」が、2は「予約」が決定打となった。
だがP10の3以降に手をつけたところ、これは一筋縄ではいかないと思った。手を変え品を変え…って「井桁」と「予約」しかないけど、コツコツ候補を減らしていくしかないと感じた。難易度的には10あるいは10+と言われても驚かない。油断してるとあたかも平成ライダー第3作『仮面ライダー龍騎』の主人公・城戸真司が最終回直前でモンスターに…やめとこそれこそ必然性ないので。
今回はP10の3を取り上げる。難易度は Level9、作者は アラームじ さん、初期値を背景色黄色で示す。
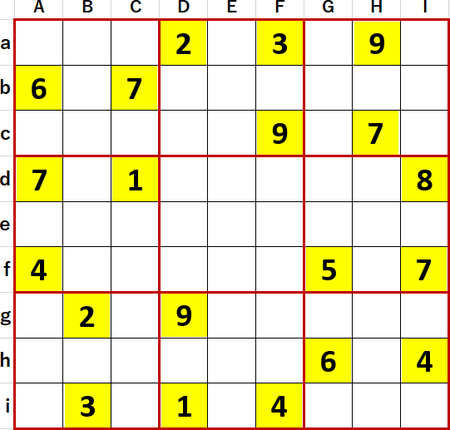
まずはローカル呼称「2択先書き法・改」にて初等解法にて埋められるマスを埋め、埋められないマスには候補として入りうる数字のメモ書きを書き尽くしてみる。
そうするとC列にCa・Chの5・8予約あるいは隠れ2国同盟がすぐに見つかった。Cc・Ce・Cfの2・3・9 3国同盟と言ってもいい。行、列、3×3ブロックで確定マスがM個ある場合、N国同盟が成立していれば同時に必ず隠れ9-M-N国同盟も成立している。
「隠れ同盟」と「影の同盟」表記揺れあるな。今さら統一できないから気にしないことにしょう。
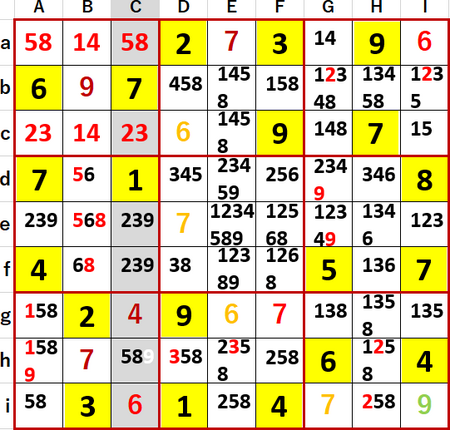
同盟は同盟国以外のマスから候補を消し、隠れ同盟(影の同盟)は同盟国から候補を消す。Chの9が消えたことにより、下段左側3×3ブロック中で2択の片割れだったAhの9が確定する。
この9をきっかけにローカル呼称「一気通貫」によりHhに1が確定し、2の下段右側3×3ブロック中の2択片割れが消えたことによりHiに2が確定する。

もしこれだけで多重選択の連鎖的解消が始まり最終形が導出できたのであれば「必殺技1発で倒せた」と比喩するところである。難易度レベルによっては、そうした問題もある。
だが超激辛最弱とは言えLevel9では、そうはいかない。
次に見つけたのはHb・Hgの5・8隠れ2国同盟だった。Hd・He・Hfの3国同盟と言ってもいい。

この結果確定したセルはなかったが、いくつか候補が消えたことによりGb・Ib・Gg・Igに3の列方向井桁(X-Wing)が出現した。この結果、Gd・Ge・Heの候補から3を除外できた。
列方向井桁が発覚すると同時に行方向井桁が、行方向井桁が発覚すると同時に列方向井桁が発覚することがある。行方向井桁は同じ列の候補を消し、列方向井桁は同じ行の候補を消すが、両者が消す候補は同じである(ローカル呼称「井桁ケンカせずの法則」)。この場合、(ACDEH・cdefh)の5連井桁が見つかった。
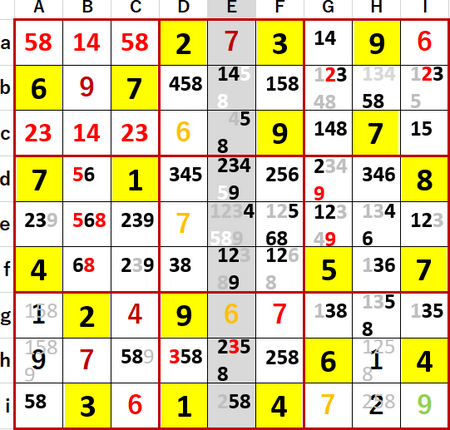
次図には3が飛車にらみを効かすマスを灰色で、井桁を構成するマスを濃い橙で、井桁により候補が除外できるマスを薄い橙で着色している。
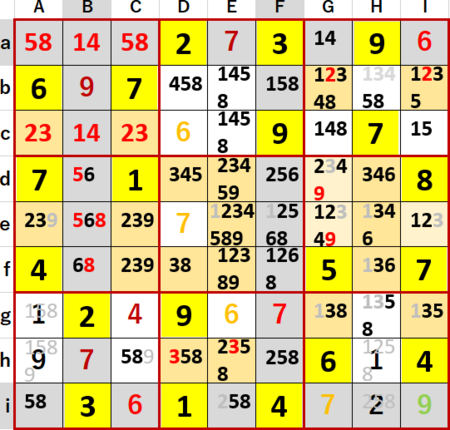
この候補削減を受けて、左側上段3×3ブロック中で2・3隠れ2国同盟または1・4・5・8 4国同盟が、f行で3・6・8 3国同盟または1・2・9 隠れ3国同盟が発覚した。

そうすると中段左側3×3ブロックで3はe行にしか存在しなくなるから、ニコリさん呼称「いずれにしても理論」により中段中央および中間右側3×3ブロックのe行の候補から3が除外できる。
次図は候補削減にはつながらない、すなわち寄り道でしかないが、ちょっと面白い現象が起きたのでスクリーンショットを撮った。
再度3の井桁をチェックしたところ、Ac・Cc・Ae・CeおよびGb・Ib・Gg・Ibの単純井桁ならびに(DEH・dfh)の3連井桁が確認できた!
一度に3つの井桁! こんなこともあるんだ。
ちなみにそれぞれの井桁の交点となるマスの候補に3はないため、すなわち井桁により削減可能な候補がないため、いつもやる「行方向井桁」「列方向井桁」の分類はこの場合不可能である。
なんで3の井桁の再チェックをしたかというと、候補がごっそり消えたのでこれで連鎖的解消につながらないかと期待したからである。2枚上の図の5連井桁が2つに分割されたということだが、期待は外れた。

結論を急ごう。井桁のチェックはすべての数字について行わなければならない。1の井桁をチェックしたところ、Ecから候補が削減できた。
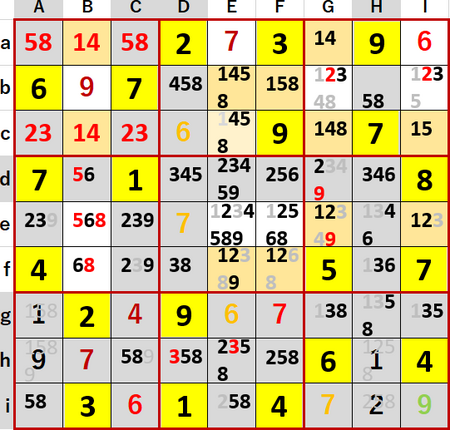
4の井桁をチェックしたところ、やはりEcから候補が削減できた。

両者の結果を受けてE列の5・8 2国同盟が出現し、これをきっかけにようやく多重選択の連鎖的解消が始まった!
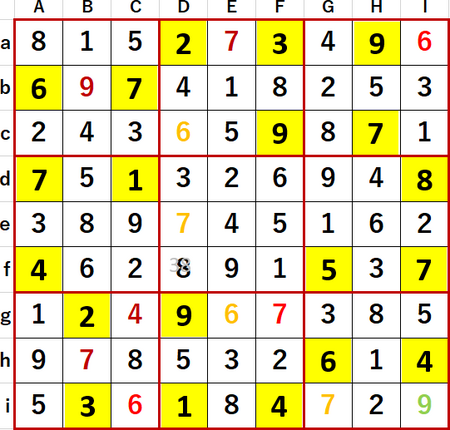
最終形を示す。Solutions P102と一致している。
同ページのヒントには、こう書いてあった。
Ac・Cc…2・3予約
Ba・Bc…1・4予約
Aa・Ai…5・8予約
1行目、2行目は2枚目の図に反映されている。3行目は最後から2枚目、最初から数えると10枚目の図に対応している。
途中の説明、すっ飛ばし過ぎじゃね? つか繰り返しになるが、超激辛最弱のLevel9にしては難しすぎね?


![仮面ライダー龍騎 Blu-ray BOX 1 [Blu-ray] 仮面ライダー龍騎 Blu-ray BOX 1 [Blu-ray]](https://m.media-amazon.com/images/I/61IbjQBpQRL._SL500_.jpg)