自己満足的数独(ナンプレ)のプレイ記録である。前回はこちら。
初めて見るケースが出現したので、記録に残す必要を感じた。誰にとって必要かというと、自分以外には思いつかないが。
初めて見るケースといえば前回記事の「1度に3つの井桁」だってそうだったし多数あるが、先に書いてしまうと一つの空白マスに1から9までの9つの数字がすべて候補に残るというケースに遭遇したのだ。自分の記憶違いでなければ初見である。
だがそれを記述すると分量的にはあっけないくらい少なく、体感した苦労と見合っていないのが悔しい。これも他人には関係ないことだが。だけど解くのに苦労したということが少しでも伝わらないかと、この間〔かん〕で手ごわいと感じた別の問題について述べた上で、後半で現象が現出した問題について述べる。やっぱ伝わらないか。
まずは解くのに苦労した別の問題の方から。ニコリ『超激辛数独2』P33の26。Levelは10に突入している。作者は printf さん。初期値を背景色黄色で示す。

ローカル呼称「飛車にらみ」など初等的に確定できるマスは確定し、確定できないマスには候補として入りうる数字をメモ書きしたのが次図。確定した数字には、確定した順番にExcelカラーパレットの左からフォント色を与えている。メモ書きは同一3×3ブロック中で2択となる数字については、重要情報なのでフォント色を赤にしている。

この状態で、一晩寝かせた。解決の糸口は、A列で3、6、7、8の4国同盟ないし1、2、9の隠れ3国同盟を発見したことだった。

M個の確定マスがある行or列or3×3ブロックでN国同盟が成立していると、同じ行or列or3×3ブロックには隠れ9-M-N同盟が必ず成立している。N国同盟は同盟に加入していないマスから候補の数字を消し、隠れ同盟は同盟に加入しているマスから候補の数字を消す。
この結果、下段左側3×3ブロックで片割れが消えた3がChに確定した。
さらに左側3×3ブロックで7につきローカル呼称「2の2の3」が適用可能だった。

すなわち中段と下段の左側3×3ブロックでは、7がB列とC列にしか残っていない。だから上段左側3×3ブロックでA列以外に7を入れると、必ず中段と下段の左側3×3ブロックで7を入れられるマスが不足する。よって上段左側3×3ブロックのB列、C列の候補から7が除外できる。
これでCcに4が確定し、ここから多重選択の連鎖的解消がスタートした。最終形を次図に示す。Solutions P108と一致している。

同ページのヒントには
Ad・Ah・Ai…1・2・9予約
3・7…Aa・Ab・Ac→Bc・Cc…4・5予約
と書いてあった。
1行目は2枚目(3枚上)の図に示した1、2、9隠れ3国同盟に対応する。
2行目は3と7がA列にしか入れられないという意味だろう。3枚目(2枚上)の図に対応すると思われる。断言しないのは、よくわからないからである。「Ccに4が確定する」と言った方が早えーだろとも思うし、さりとてそれを超激辛シリーズのヒントの文法ではどう記述したらいいのかもわからない。
つまるところ、私は『超激辛』シリーズ2大解法のうち、「井桁」より「予約」(N国同盟) の方が苦手だと言いたかった次第である。井桁のほうはローカル呼称「井桁塗り分け法」という攻略法を開発したが、予約のほうは効果的な攻略法をまだ見つけられないでいる。ちなみにスキップした問題の大半は、主に「井桁塗分け法」で解いた。
ということで、今回の主題となるP40 33の初期値を示す。作者はやはり printf さん。難易度もやはりLevel10。

数字が確定できるマスは確定し、確定できない数字には候補の数字のメモ書きを書き尽くそうとしている過程のスクリーンショットを1枚だけ貼る。下段中央3×3ブロック中の1、5、7予約(3国同盟)ないし2、4、9予約(隠れ3国同盟)は、比較的容易に見つかった。
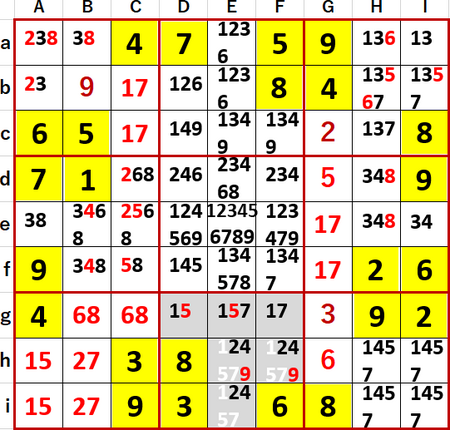
先に述べた通り、この問題で最も特徴的だと感じられたことは、Eeの候補に1から9までのすべての数字が残ったことだった。こんなことは過去の記憶にない。

候補の数字が多いということは、予約を見つけ出すのも難しくなるということだ。
その意味では、この問題の難度はmaxのはず。しかし『超激辛』シリーズではLevel10の上にまだLevel10+があるというのが解せない。
そしてこの問題の場合、そのEeを含むe行に予約を見つけたことが、解決に結びついたことも特徴的だと感じた。正面突破を強いられたわけだ。

e列に3、4、8の3国同盟ないし1、2、5、6、7、9の隠れ6国同盟が発覚し、これによりBeに6が確定したことを手がかりに、多重選択の連鎖的解消が始まった。
もっとも、一番ありふれた2国同盟を見つけたとき、いちいち隠れ7国同盟なんて言わないから、隠れ6国同盟には言及しなくてもよかったかも知れない。
最終形を示す。Solutions P110と一致している。

同ページのヒントには
Bh・Bi…2・7予約
Ae・He・Ie…3・4・8予約
Df・Dg…1・5予約
と書いてあった。
1行目は4枚上の図に反映済みである。
2行目が今回主題の2枚上の図に対応している。
3行目は、よくわからない。多重選択の崩壊の過程で必要となる局面があったのかも知れないが、覚えていない。
スポンサーリンク
