自己満足的数独(ナンプレ)プレイ記録である。前回はこちら。
ニコリさんの「超激辛」シリーズには難易度Level9、Level9+、Level10、Level10+の4段階の問題が収録されている。前3者の問題数は少なく、難易度最高のLevel10+が半分以上を占めている。「超激辛シリーズ」の主役はLevel10+なのだろう。
今やっている『超激辛数独4』全91問中、Level9は5問で終わりで、6問目からLevel9+に突入した。それを記念(?)して、エントリーを立てる。
今回は3問アップする。まずP13 6。作者 我ヒトにあらず さん。
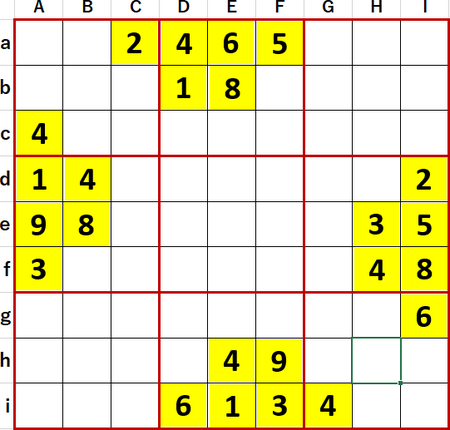
初等的に埋められるマスを埋め、埋められないマスには候補の数字を書き尽くした状態を示す。
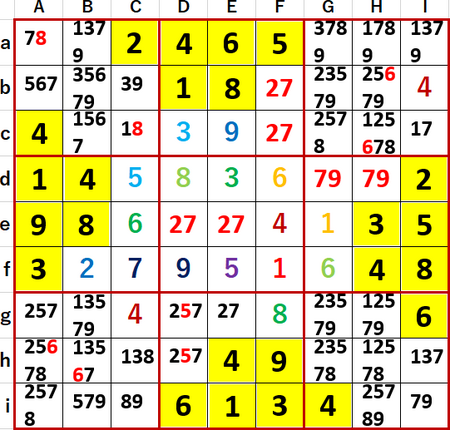
g行に2・5・7 3国同盟が見つかったので、Bg・Gg・Hgの候補からこれらの数字を除くことができた。
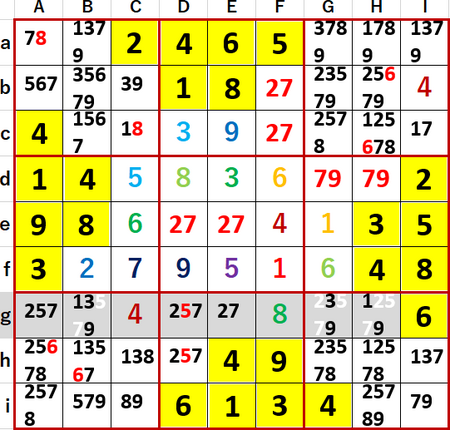
すると下段右側3×3ブロックに1・3・7・9 4国同盟が発覚した。これによりGh・Hh・Hiの候補から、これらを除くことができた。
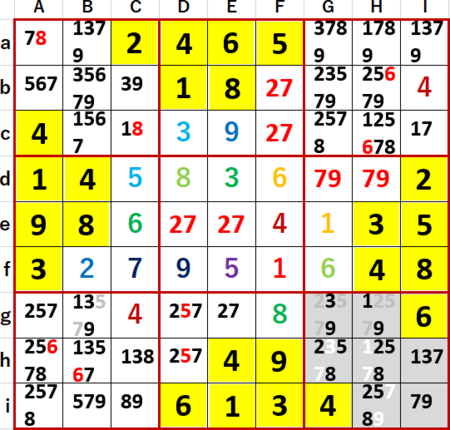
そうすると同ブロックで7はIh・Iiどちらかにしか入れることができない。よってニコリさん呼称「いずれにしても理論」によりI列のこれら以外のマスには7が入れられないことになり、Icに1が確定した。
この1をきっかけに、多重選択の連鎖的解消が始まった。
最終形を示す。巻末のSolutions P103と一致している。
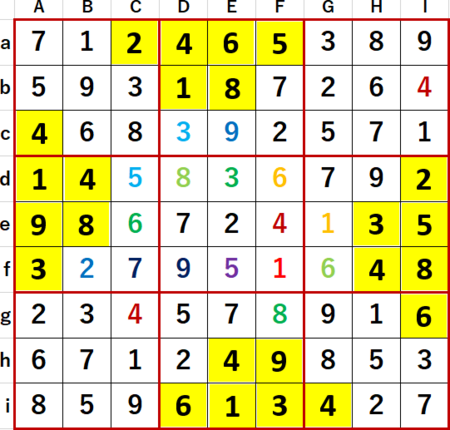
同ページのヒントには
Bg・Gg・Hg…1・3・9予約
Gh・Hh・Hi…2・5・8予約
7…Ih・Ii…Ic→1
と書いてあった。
1行目は2枚目(3枚上)のスクリーンショットに、2行目は3枚目(2枚上)のスクリーンショットにそれぞれ対応しているが、N国同盟ではなく隠れN国同盟のほうで記述してある。
3行目は「いずれにしても理論」である。
次にP14 7。作者 福神ヅケ さん。
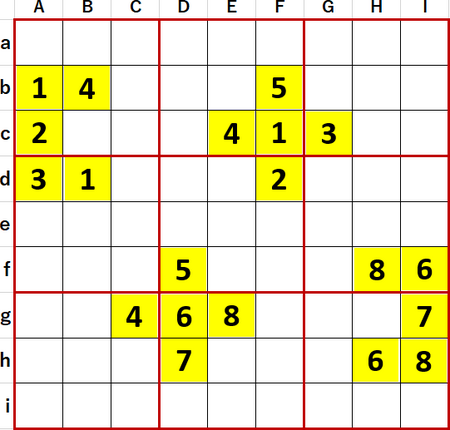
初等的に埋められるマスを埋め、埋められないマスには候補の数字を書き尽くした。この問題で特徴的だったのは、この段階で下段左側3×3ブロックに2つの2国同盟と1つの3国同盟が発覚したことだった。
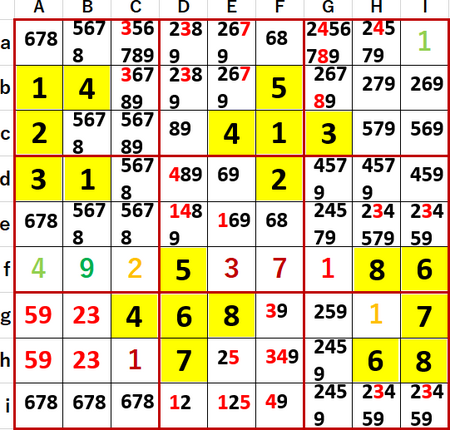
ただし、その次の段階でG列のGa・Gbの6・8隠れ2国同盟を見つけるのは、ちょっと苦労した。
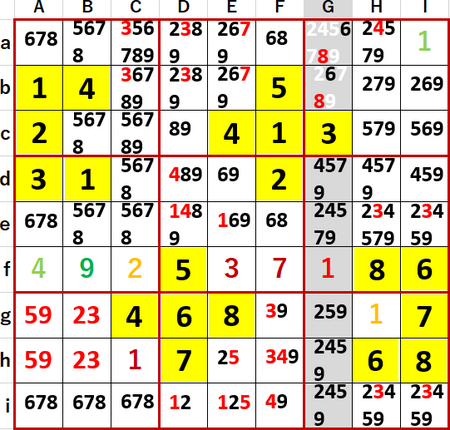
この隠れ2国同盟は上段右側3×3ブロックからも候補の数字を消すことに加えて、新たにa行にFa・Gaの6・8 2国同盟が発覚した。
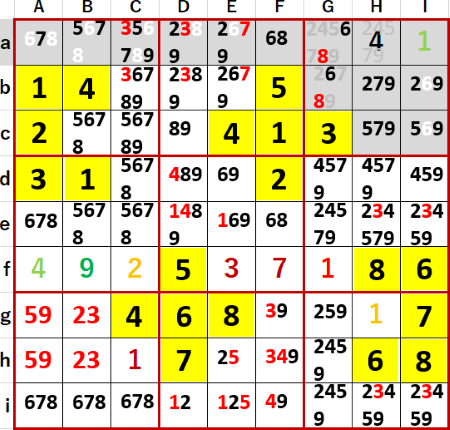
Aaの7の確定をきっかけに、多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P103と一致している。
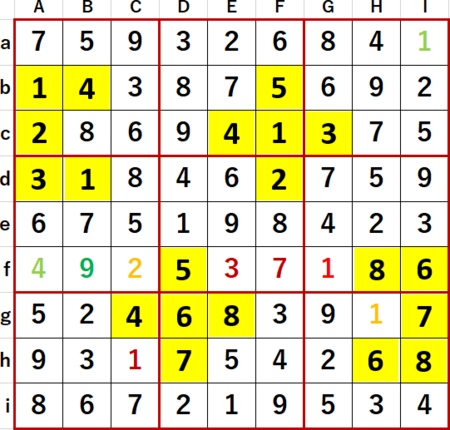
同ページのヒントには
Fa・Fe…6・8予約
Ai・Bi・Ci…6・7・8予約
Bg・Bh…2・3予約
Ga・Gb…6・8予約
Fa・Ga…6・8予約
と書いてあった。
1行目、言われてみれば確かにそうなっているが、使わなかったぞ! 役に立ったのかコレ?
2行目と3行目は4枚上のスクショに反映済みである。
4行目は3枚上の、5行目は2枚上のスクショに、それぞれ対応している。
もう1問。P15 8。作者 3次関数 さん。
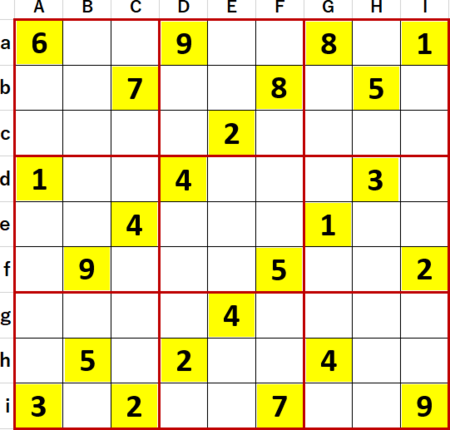
初等的に埋められるマスを埋め、埋められないマスには候補の数字を書き尽くした。

A列に7・8・9 3国同盟が見つかった。

これを受けて上段左側3×3ブロックに2・3・4・5 4国同盟ないし1・8・9 隠れr3国同盟が見つかった。
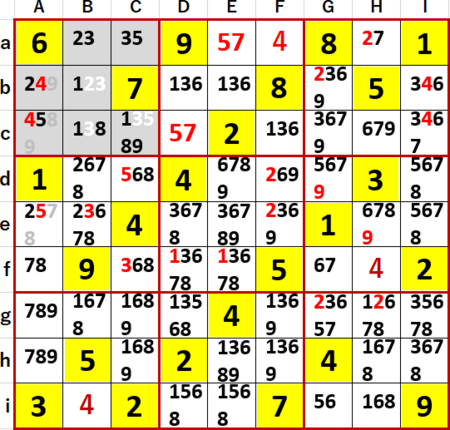
Bbに確定した1をきっかけに、多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P103と一致している。
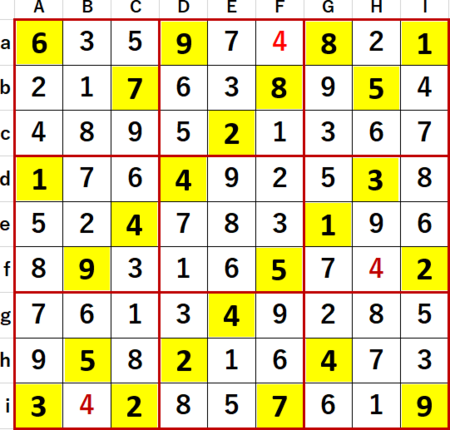
同ページのヒントには
Ab・Ac・Ae…2・4・5予約
とだけ書いてあった。3枚上のスクショの、隠れ3国同盟の方での表記である。
そゆえば『超激辛4』では、ここまで「井桁」解法を使ってないな。そのうち出てくるだろうけど。
