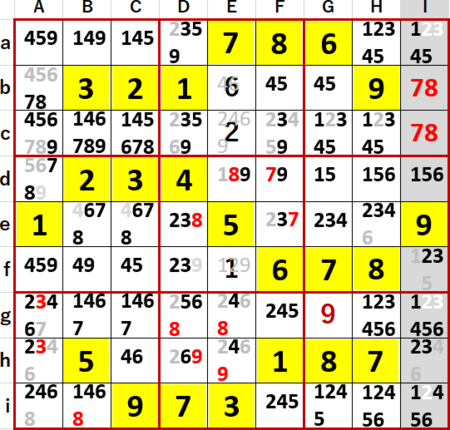
自己満足的数独(ナンプレ)のプレイ記録である。前回昨日付け拙エントリーの最後で「予約」あるいは「N国同盟」解法において、N国とN+1国の複数の解釈が同時に成り立つケースが発生し驚いた旨を書いた。
そんなこと、そうそうあるんだろうかとN国同盟を主力として解いた別の問題を、もう一つチェックしてみた。タネ本『超激辛数独2』のP51 44。難易度Level10、作者は アラームじ さん。初期値を背景色黄色で示す。
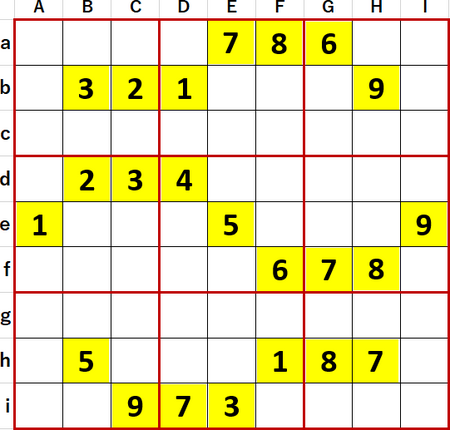
問題自体の難度は、昨日の40よりこの44の方が高かったように感じた。最終形を導くまでに、かかった手数が多かったのだ。
初等的解法で埋められるマスは埋め、埋められないマスには候補の数字を埋め尽くしたのが次図。埋められたマスはGgの9だけだった。井桁解法を適用できる数字はなかった。
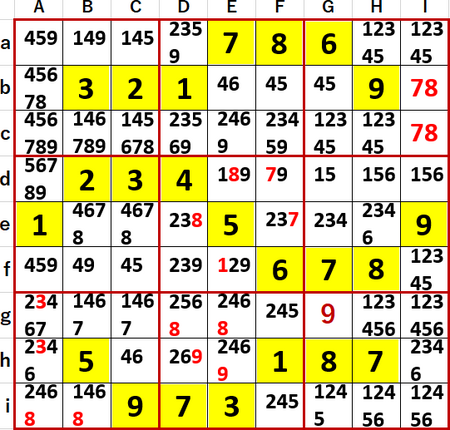
この問題でも、N国同盟が同時にいくつか発覚した。

b行の4・5 2国同盟は一目でわかった。
他にd行と中段右側3×3ブロックの1・5・6 3国同盟、およびF列の2・4・5 3国同盟を見つけた。
最後の一人反省会で改めて述べますが、まだ見落としがあります。
b行の4・5 2国同盟は、Ebの6を確定した。
d行の1・5・6 3国同盟は、中段中央3×3ブロックの1の2択の片割れを消すので、同ブロックEfの1が確定した。
それらを反映させ、消せる候補を消して整理したのが次図。

中段右側3×3ブロックとf行に4・5・9 3国同盟が発覚した。
あとでやる一人反省会で言及するが、f行は2・3 隠れ2国同盟でもある。
前図を受けてA列に7・8 2国同盟が発覚した。
また中段中央3×3ブロック中で2はD列にしかないので、上段中央3×3ブロックと下段中央3×3ブロックのD列の候補から2を除くことができた。ニコリさん呼称「いずれにしても理論」である(『超激辛数独2』P3

上段中央3×3ブロック中のD列の候補から2が消えたことにより、同ブロック中のマスで2が候補に残るのはEcだけになった。よってこのマスに2が確定した。
これを受けh行に2・3 2国同盟が…
I列に、やはり2・3 2国同盟が発覚した。
この結果、上段右側3×3ブロックで2が候補に残るマスはHaだけになり、このマスに2が確定した。
a行で候補に3が残るマスはDaだけになり、このマスに3が確定した。
これでようやく多重選択の連鎖的崩壊が始まり、最終形を導くことができた。
Solutions P112と一致している。

今回はヒントとの照合は省略する。以下、一人反省会である。
わりと多くのN国同盟を使ったから、一つくらい前回40のようなN国同盟とN-1国同盟の複数解釈が成り立つケースがないか探してみたが、そういうものは見当たらなかった。
もっとたくさんに当たるのならともかく、1問くらいじゃムリか。
代わりに次の見落しを見つけた。2枚目の、候補の数字を埋め尽くした状態の続きであるが、f行に4・5・9 3国同盟あるいは1・2・3 隠れ3国同盟が成立しているのを見落としていた! 消える前の1は、2・3にくっつけることができたのだ。
仮にここから進めたら、どうなるだろうとやってみた。
しかしd行1・5・6 3国同盟(7・8・9 隠れ3国同盟)により中段中央3×3ブロックEfの1を確定させると(3枚目の図に相当)、以降はf列2・3 2国同盟と同じ状態に収斂することがわかった。
前回40もそうだったが、安易な喩えだけれど最終形という頂上が1つなので、それを目指す登山ルートは複数あってもいずれ収斂するものかも知れない。

山登りのイラスト(男性) | かわいいフリー素材集 いらすとや より。規約の範囲で改造しています。
追記:
N国同盟とN+1国同盟の解釈が同時に成り立つケースは P75 68 で2例目を見つけた。