自己満足的数独(ナンプレ)プレイ記録である。前回はこちら。
タネ本のニコリ編著『ポケット数独 上級篇1』(ソフトバンク クリエイティブ) も残り僅少となり、次は何をやろうか少し考えた。1があるってことは2をやればいいのだが、パターンがわかってきて解く時間が短くなり、せっかくだからもう少し難しい問題があればチャレンジしたいと思ったのだ。
折よく「はてなブログ」の「おとなり日記」という機能が、id:muranaga さんのこちらの記事を紹介してくれました。私よりずっと長く数独を解かれている方のようです。突然のIDコール、失礼します。
ニコリさんのシリーズにはいくつものタイトルがあるが、『上級篇』のほかに『激辛数独』というシリーズがあり、それが何年か前に易しめの『難関数独』と最難関の『超激辛数独』に分かれたようだ、とのことだった。
ちょっと迷って、この中ではいちばん古い『激辛数独1』というのをアマポチしてみた。『難関』と『超激辛』に分かれたということは、どちらのレベルの問題も収録されているということであろうと考えたのだ。
届いた本が手元にある。体裁は『上級篇』とそっくりだった。まえがきにあたる数ページの『数独の解き方』に続いて、ひたすら問題。上級篇と同じ105問あって巻末に SOLUTION(解答編)が置かれていた。
『上級篇』との違いは、Levelが2から10までの9段階に分類されていることと(『上級篇』はLevel7~9の3段階)、作者の名前またはペンネームが載っていることだった。
『激辛』でLevel2? といぶかしく感じたが、実際の難易度は解いてみなきゃわからない。
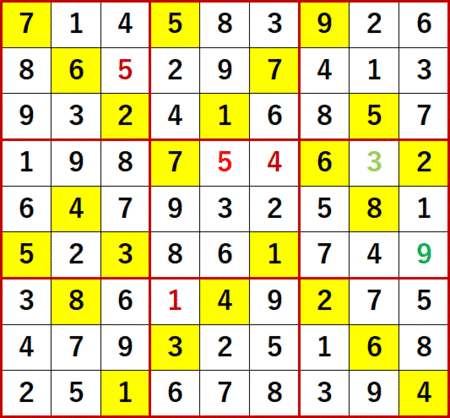
まずは『上級篇』のコンプリートを目指そう。今回解いたのは P106の99。Level9である。
初期状態を背景色黄色で示す。

解法は少しずつ手直ししている。前回までの拙記事では1から順に初等解法で埋められるマスを埋めると書いたが、初期値に出てくる数字の数がいちばん多いものから手をつけたほうが手数がさらに若干省けることに気づいた。
この問題の場合1、2、4、5、6、7、8がそれぞれ3つでタイか。3つばっかりだな。
そういう場合は、登場回数が最も少ない数字から最も遠い数字を起点とするのだ。
いちばん少ないのは9の1つ…1から始めるしかないじゃないか!
この問題の場合、たまたま1から始めるのがいちばん合理的と判断ついたということで、何の問題もない。
1の飛車にらみによって1つのマスが埋まった。1の入る候補の空白マスが9×9ブロック中で2択に限定される場合は、1巡目からフォント色赤でメモする。「2択先書き法・改」とローカル呼称している解法である。
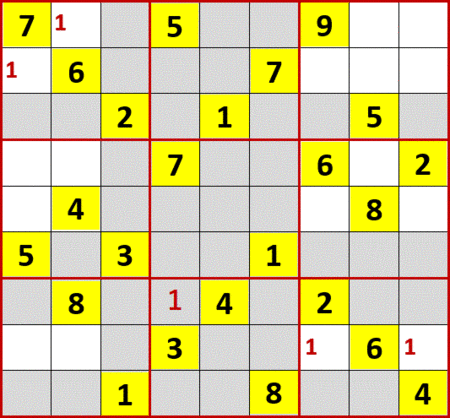
2では1巡目から埋められるマスはなし、いくつかの2択をメモ書きした。
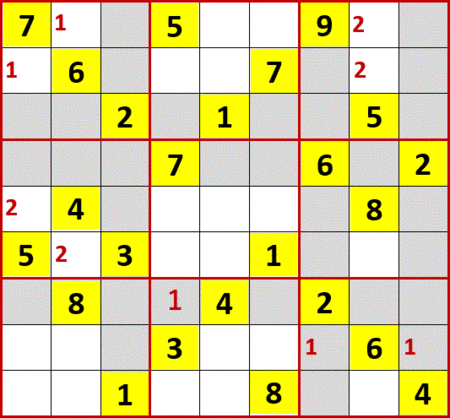
3は埋められるマスも2択となるマスもなかった。
4、5、6、7について同様の操作を行った。
8で劇的なことが起きた。
左側中段3×3ブロック中上から4行に8が2択となるマスが横に並んでいるので、google:ロックされた候補 と呼ばれる解法により、他の3×3ブロックの上から4行目には8が入れられないことがわかる。
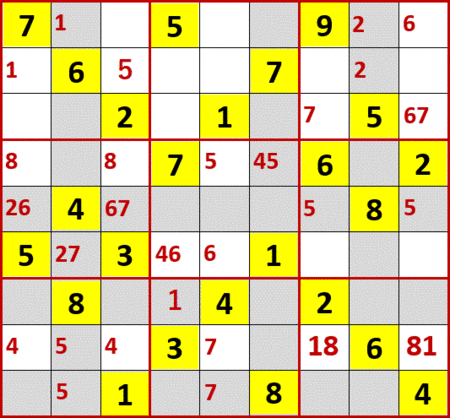
これにより中段中央3×3ブロック中下から4行目左から4列目と5列目に、6と8の「2国同盟」が成立する。この2つの空白マスに入る数字は、6か8に限定されるということだ。
2国同盟は重要なので、目立つようにフォントサイズを拡大している。
そうすると4はどうなるかというと、6と8の二国同盟が成立しているマスには入れられない。もし入れたら、6と8を入れる空白マスが不足するからだ。つまり4は、これらのマスからはじき飛ばされる。
よって上から4行目右から4列目に残った4の2択の片割れが、めでたく確定される。
こうして確定した4が、5の2択の片割れを消す。そうすると上から4行目右から5列目(左から5列目でもある)の5が確定する。
前回同様、初等解法で確定した数字はExcelのカラーパレットの順にフォント色を変えている。あとから思考過程を追跡するためだ。
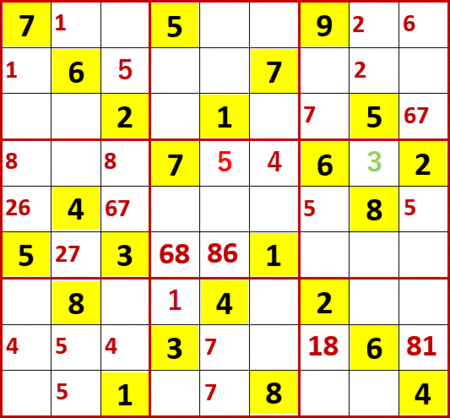
これで終わりではない。上から4行目に着目すると、左側中段3×3ブロック中の空白マスには3を入れることができない。同一ブロック中に3があるからだ。
そうすると同行の右から2列目に最後に残った空白マスに、3が確定するのである。「一気通貫」とローカル呼称している解法である。
どや!
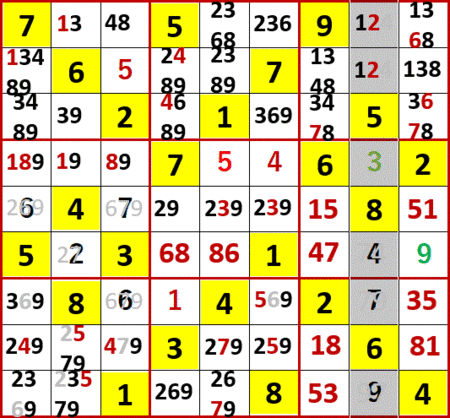
こんなふうにして、初等的に埋められるマスはすべて埋め、空白マスには入れられる候補の数字をすべてメモ書きした状態が、下図である。
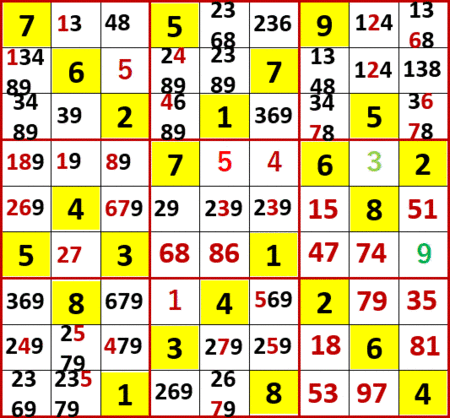
初等的でない手がかりで、最初に気づいたのは中段中央3×3ブロック中の、上から5行目(下から5行目でもある)の2、3、9の「変形3国同盟」である。
他の3×3ブロックの上から5行目の空白マスには2、3、9は入れられない。もし入れたら「変形3国同盟」を構成しているマスに入れられる数字が不足するからだ。
これにより最左列上から5行目の空白マスに入る数字の候補から2と9が消え、6だけが残った。つまりこのマスの6が確定した!
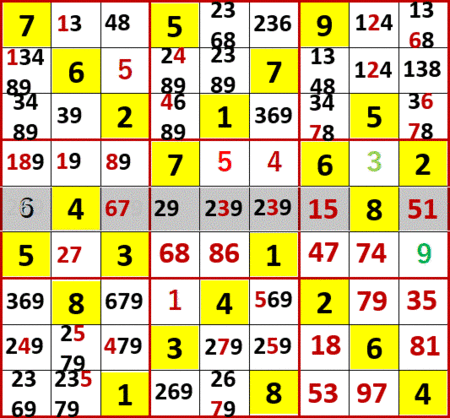
確定したマスのメモ書き数字は、フォント色を目立たぬ灰色にして残している。ローカル呼称「候補メモ最後まで残す法」である。残す数字消す数字を間違える単純ミスはどうしても避けられないので、追跡する手がかりのつもりである。
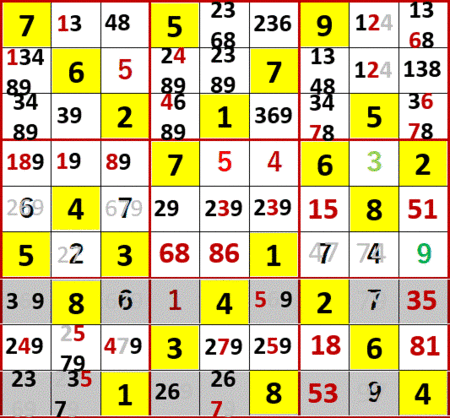
この6を足場にして、同3×3ブロック中で2と7が確定した。2択の片割れが次々と消えたということだ。
新たに確定した6、2、7は、それぞれが飛車にらみする空白マスの候補から自分と同じ数字を消す。
今の場合、効果は列方向にしか波及してないな。
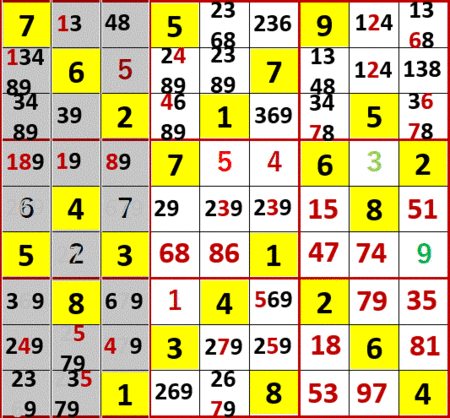
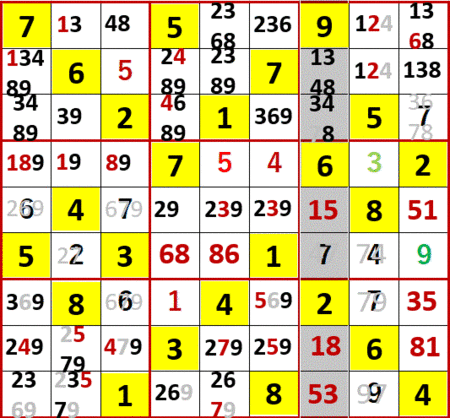
だけど左から3列目に着目すると、6が候補として残るマスは下から3行目しかなくなった。初等解法「一気通貫」である。よってこのマスの6が確定した。
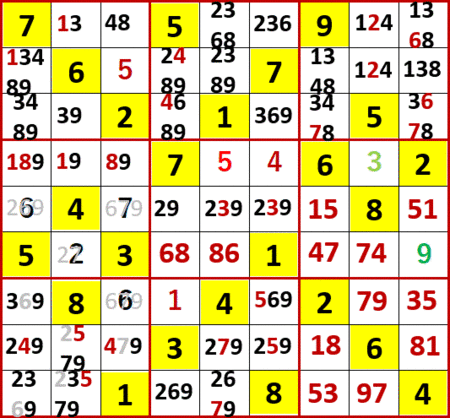
以降この6を手がかりに、候補が消えマスが確定してゆく様子を、何枚かの静止画で貼る。
最終形までは行ってない。
以前だったらgifアニメ化していたところだが、わかりにくいばかりで労多くして功少ないので、今はよすようになった。
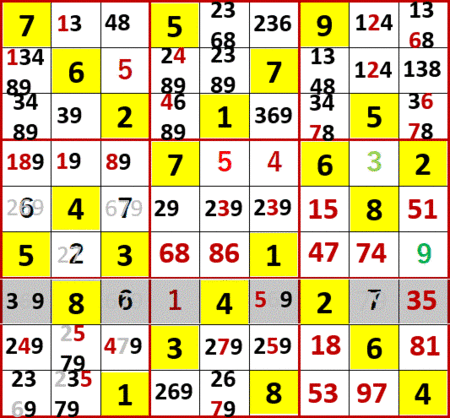
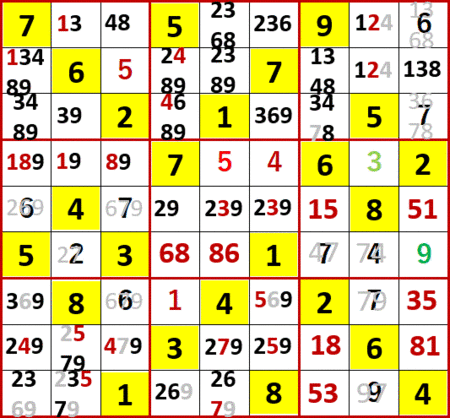
最終形を、候補数字のメモを外して貼る。ANSWERS P126と一致している。