数独(ナンプレ)の自己満足的プレイ記録の連投になります。前回の拙記事はこちら。なんだか知らないけど前回のサムネイルがペヤングの企画商品みたい。
8月から4ヶ月ばかりかけて遊ばせてもらったニコリ編著『ポケット数独 上級篇1』(ソフトバンク クリエイティブ)、ついに最後の105までやり切ってしまったので、数独ネタの連投になるがエントリーを上げたかった次第。
『上級篇1』全篇を通じていちばん難しいだろうと思ったのは、ラストの105(P112)ではなく、103(P110)じゃなかったかという気がする。しかし私の側でも慣れがあったのだろう、寝かすことなく即日解けた。
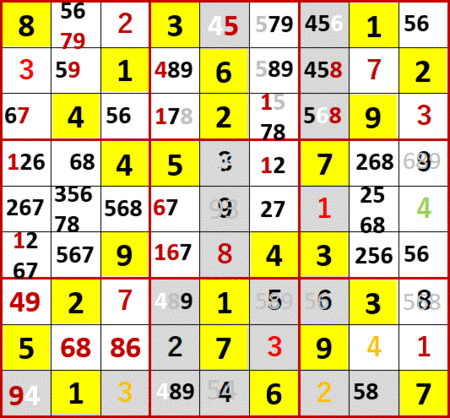
103初期値を、例によって背景色黄色で示した。

ローカル呼称「飛車にらみ」など初等解法により埋められる数字は埋め、ローカル呼称「2択先書き法・改」により空白マスに入れられる可能性のある数字のメモ書きを書き尽した状態が下図。初等解法で埋めた数字は、記憶のトレースの手がかりのためExcelカラーパレットの順にフォント色を変更している。候補の数字が入る空白マスが同一3×3ブロック中で2択になる場合は、メモ書きのフォント色を赤にしている。
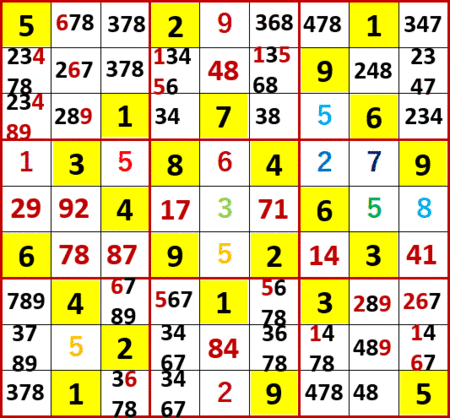
のっけから大技が必要になった。ローカル呼称「2の2の3」である。『上級篇1』を解くに当たって今のところ最後に開発した解法なので、自分の中では「最後の技」と呼んでいる。
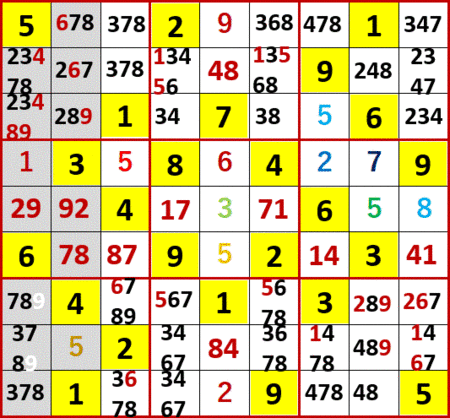
左側の上段、中段、下段3×3ブロック中の9に着目する。上段、中段は左から1列目と2列目にしか9はないが、下段だけは左から3列目にも存在する。もし下段3×3ブロックで1列目に(この図の場合存在しないが、もしあれば2列目にも)9を入れたら、上段か中段3×3ブロックで9を入れられる列が不足する。よって下段では左から3列目に9を入れるしかなく、1列目の(もしあれば2列目も)9は候補から除外することができる。
これが解法「2の2の3」の考え方である。
これにより、左から3列目、下から3行目の9が確定する。
この9が同3×3ブロック中の2択の6の片割れを消すため、左から3列目最下行の6も確定する。かように同一ブロック中での2択は重要である。
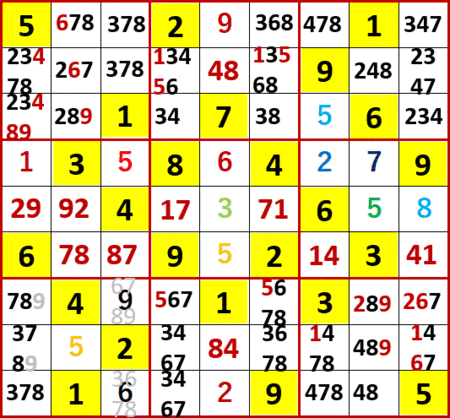
確定した9と6は、横にらみによりいくつかのマスから自分と同じ数字の候補を消す。
縦方向には消せる候補はなかった。
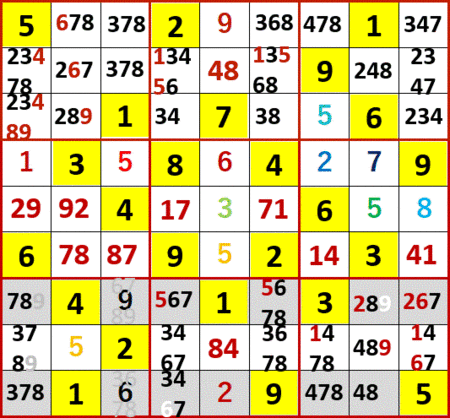
右側下段3×3ブロックで、2択の9の片方が消えたので、下から2行目右から2列目の残りの9が確定する。
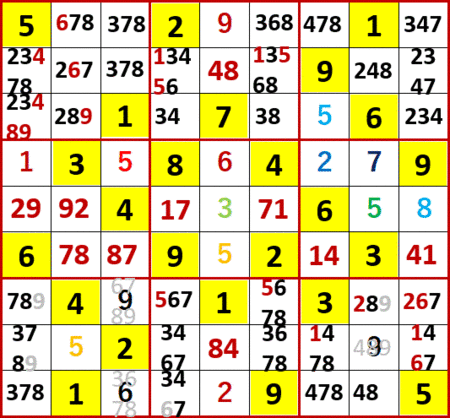
これらを踏まえて、初登場の解法パターンが出現した。今度は上段の左側、中央、右側3×3ブロック中の4に着目する。左側と中央の3×3ブロックでは4は2行目と3行目にしか存在しないが、右側3×3ブロックでは最上行にも存在する。
右側ブロックで2行目か3行目に4を入れたら、左側と中央どちらかでは2行目か3行目に4を入れることができなくなる。よって右側3×3ブロックの2行目と3行目の候補から4を除くことができる。
先ほどの「2の2の3」を列バージョンとすると、こちらは行バージョンである。
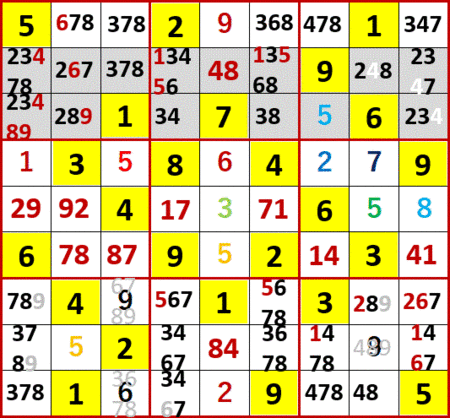
さらにこの結果を踏まえて、右側上段、中段、下段3×3ブロックの4に着目する。
上段ブロックの4のいくつかが消えたため、上段と中段では4の候補は右から1列目と3列目にしか存在しなくなった。下段3×3ブロックでは1列目から3列目まで、すべての列に4が存在する。よって下段ブロックでは4は右から2列目にしか存在することができず、よってagain最下行右から2列目の4が確定する。
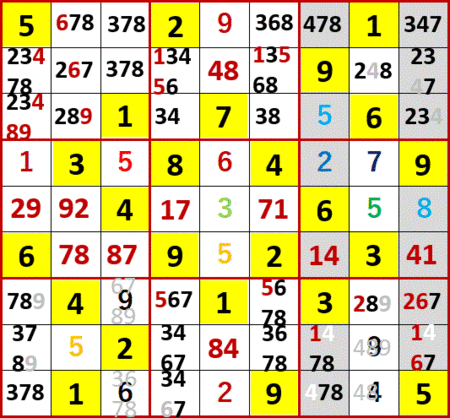
つまり「2の2の3」をカスケード使用(連続使用)したのだ。見落しがなければ『上級篇1』中でそういう解法が必要になったのは、この問題だけだった。
だが同じ解法のカスケード使用は、これまでにもたびたび出現したので戸惑うことはなかった。
しかし『上級篇』を順を追って解いていったからできたことで、もし初見でこんな問題に当たったらぜってー解けなかったと思う。
ただし最終形に行きつくには、もうひと工夫が必要だった。
上から2行目に着目すると、最左列の2と4、左から5列目(右から5列目でもある)の4と8、右から2列目の2と8が「変形3国同盟」を構成していることに気づいた。
上から2行目の他の空白マスのいずれかに2か4か8を入れると、3国同盟を構成しているマスに入れる数字が不足する。よって3国同盟以外の空白マスに入るう数字の候補から、2と4と8を除外することができる。
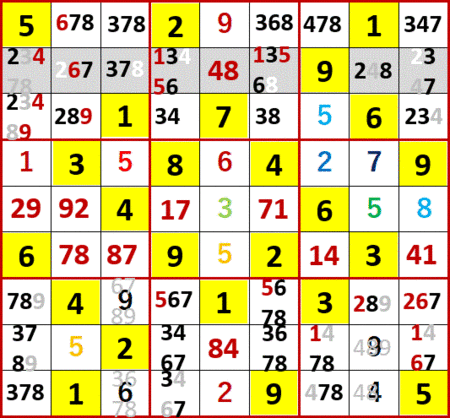
この行ではさらに最右列と左から3列目に3と7の2国同盟が成立し、これらの結果右から2列目上から2行目の6が確定する。
この6が確定されるマスや消す候補を手がかりに、一気に多重選択が崩れ始めた。
思い出してみると「3国同盟」、「変形3国同盟」もけっこうな大技だった。大技というのはマスターするのに場数が必要だったという意味である。
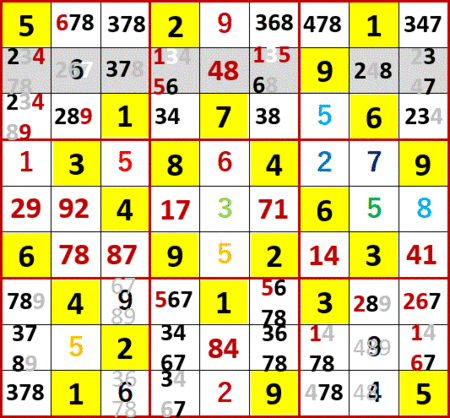
最終形を示す。ANSWERS P126と一致している。
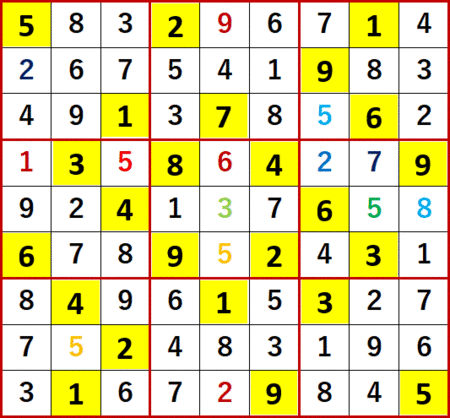
103に比べると104、105は、最終ページで出てくる問題にしては、ややこしい解法を必要としなかったように思う。
ただしあくまでややこしい解法が必要なかったというだけで、私の単純ミスなどの理由により解くのにはきっちり苦労した。この場合、苦労というのは楽しませてもらったという意味である。
次図は104(P111)の初期値である。
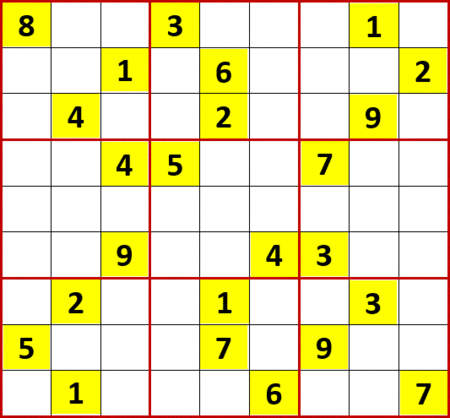
初等解法で埋められるマスを埋め、空白マスに入れられる候補の数字をメモし尽したのが次図。
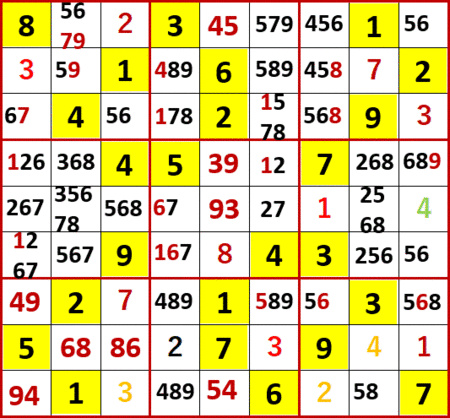
最右列の5と6の2国同盟、左から4列目の4、8、9の3国同盟が即座に目に入った。
これらの列から除外できる候補を除外すると…
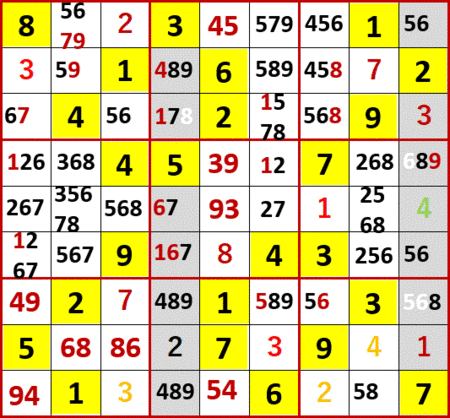
最右列下から3行目の8が確定し、この8が縦横の自分と同じ数字を候補から消すことにより…
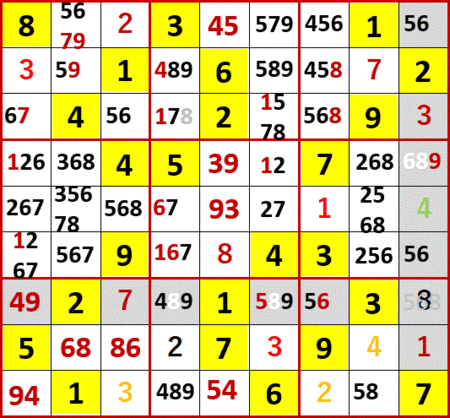
最右列上から4行目の9が確定する。9は同じ行の9を空白マスに入る候補から消す。
下から3行目では最左列と左から4列目の4と9が2国同盟を構成し、同行の他の空白マスに入る候補から4と9を消す。
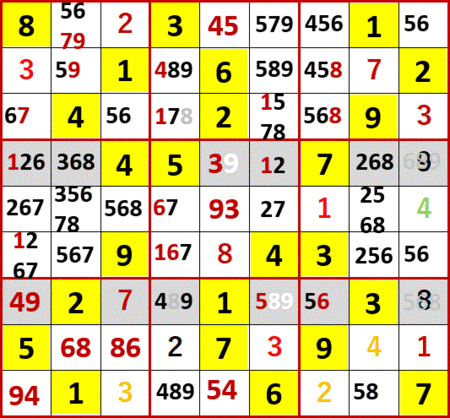
あとは多重選択が崩れるところを何枚かの静止画で。gifアニメ化は、わかりにくいのであきらめている。
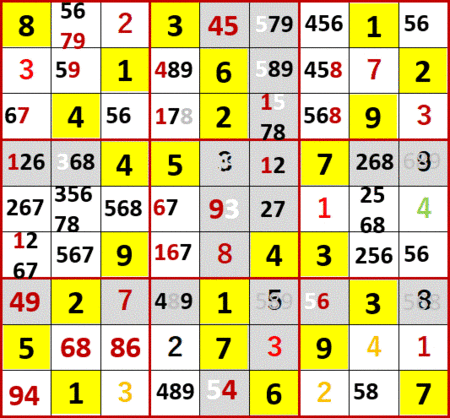
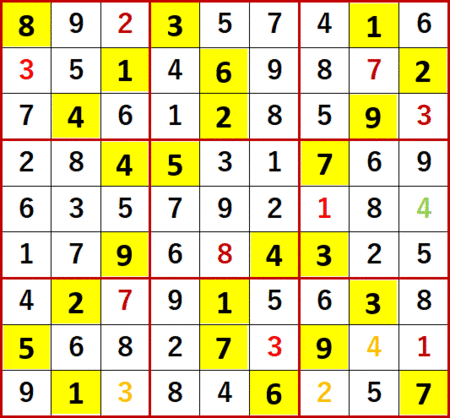
最終形。ANSWERS P126と一致している。
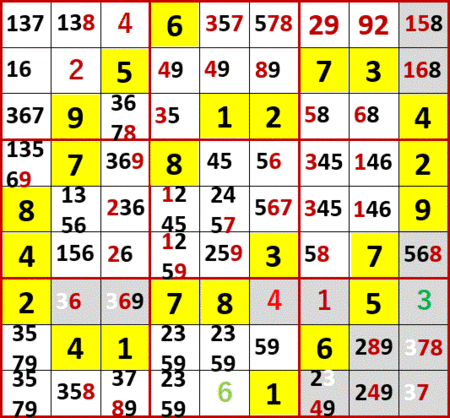
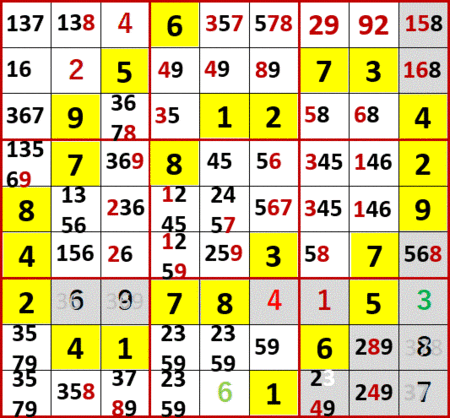
上級篇1最後の問題105(P112)は、もっと易しかった。次図が初期値。

埋められるマスを埋め、候補の数字も埋め尽そうとしたところで、最右列下から3行目にローカル呼称「総消去法」で3が確定きることに気づいた。

1と5は同一行(同一3×3ブロックでもある)にある。
2と4は同一行と同一列にある。
6は同一3×3ブロックにある。
7と8は同一行にある。
9は同一列にある。
そしてこの3を手がかりに、初等解法だけで最終形まで行きついてしまったのだ!
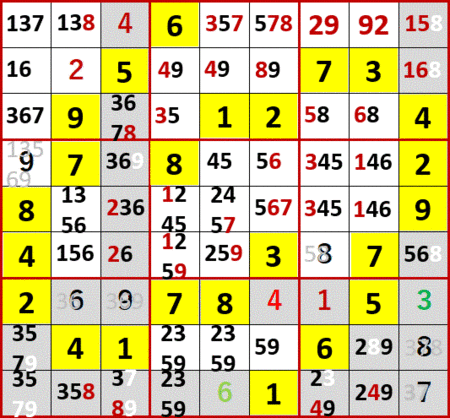
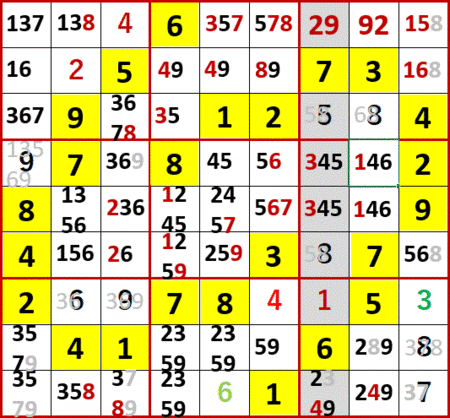
最後までは貼らないけど、静止画を多めに貼る。数独をやったことがある人には、解説いらないんじゃないかな?
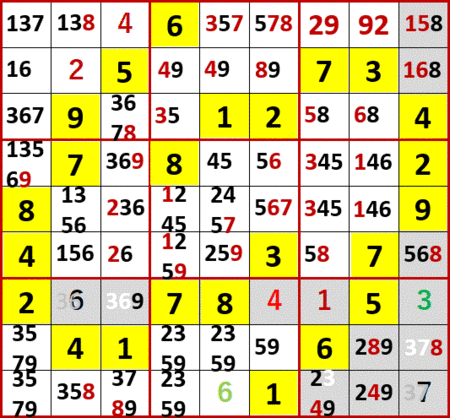
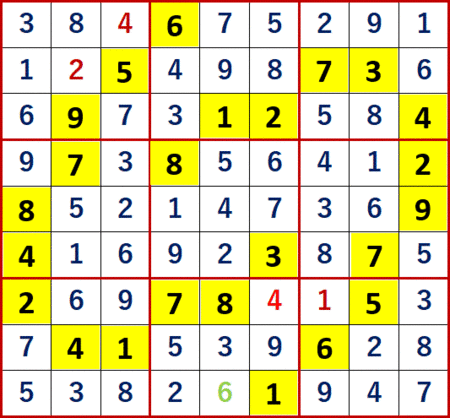
最終形。ANSWERS P127と一致している。
ものすごくヘンな感想だけど、ネットミームと化している伝説のwebマンガ『ソードマスターヤマト』最終話を思い出した。「奴は四天王の中でも最弱…」とか言ってる残りの三天王(?) が一コマでやられちゃう、あれ。
貼っていいのかな?
何故に今!?
— ギャグマンガ日和 公式 (@gagmanga_biyori) 2022年11月9日
まさかの「ソードマスターヤマト」トレンド入り🎊
これを記念して、伝説の『ソードマスターヤマト』最終話を全ページ公開✨
夢野カケラ先生はいかにして前代未聞の最終話を作るに至ったか…そして、最終話1話前に起きた「誤植事件」も語られる第85幕「ソードマスターヤマト」は無印5巻‼ pic.twitter.com/kLwWMCMn7O
そゆえばローカル呼称と称してヘンな解法の名前を毎回いちいち記しているのは、「新必殺音速火炎斬!」のような必殺技名を叫ぶ機会が現実生活ではありえないという笑えるネット指摘(?)が念頭にあるからである。
問題を解くとき「総消去法!」「変形3国同盟!」「最終解法、2の2の3!」と、思う存分脳内で技名を叫んでいるのである。脳内だけですよ! ホントですよ!
そして私にとってのベルゼバブの魔龍城は、多分こいつだろう。

