自己満足的数独(ナンプレ)プレイ記録の連投である。昨日(6/1)付拙記事ではニコリさん『超激辛数独5』序盤と言っていい全91問中9問目にして難度高い問題に遭遇したことを書いたが、続くP17 10はさらに体感難度高く感じたので、ネタにしたいと思った。あくまで個人の感想です。
最初に結論を書いてしまうと、最終局面において「2の2の3」とローカル呼称している解法の連続使用が必要となった。「2の2の3」は、決して難しいテクニックではない。また過去記事を検索すると、いちどきに行方向と列方向に同時に適用できた問題を取り上げたこともあった。しかし今回の問題がなんで難しいと感じたかというと…先走りすぎはよくないな。順を追って説明しなければ。
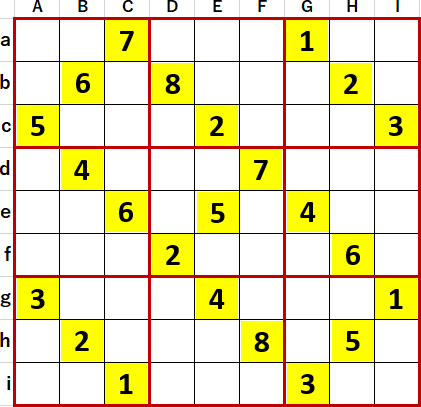
そのP17 10、作者 アラームじ さん、難易度Level9+。初期値を背景色黄色で示す。初期値に9が現れない。
弊ブログはアフィリエイト広告を利用しています
初等解法で埋められるマスを埋め、埋められないマスには候補として入りうる数字のメモを書き尽した。初期値のない9が候補に多く残った。こういう現象は、過去の問題でもしょっちゅう出てきたことがあるのだが…と伏線を埋めとこう。

まずe行De・Fe・He 3国同盟またはAe・Beの7・8隠れ2国同盟が見つかり…

この結果による候補削減を受けてAd・Afに1・9 2国同盟が発覚し…

A列と中段左側3×3ブロックから、さらにいくつかの候補が削減できた。

これによりAbに4、Bcに1が確定し、さらにいくつかの候補が削減できた。
Level9+なら、これで多重選択の連続的解消が始まるかなと思ったら、始まらなかった。
それどころか、N国同盟と井桁のチェックを何巡かおこなったが、ぜんぜん見つけることができなかった。
苦労した結果の結論のみ。候補の多い9につき、下段3×3ブロックに「2の2の3」解法が適用可能であることを見つけた。すなわち下段右側3×3ブロックと下段中央3×3ブロックの9の候補はg行とi行にしかないので、下段右側3×3ブロックの9の候補はh行にしか残らない。

そうすると中段右側3×3ブロックと下段右側で9の候補はG列とI列にしか残らなくなったので、上段右側3×3ブロックの9の候補はH列にしか残らない。

そうするとGb・Ibに5・7 2国同盟が発覚し、これによりDcに7、Daに4が確定したことをきっかけに、多重選択の連続的解消が始まった。
候補が多いと、N国同盟や井桁を見つけるのも難しくなる。しかもこの問題の場合、候補多い9に関しては結局どちらも見つからなかったことが、難しさをいや増しにした理由である、と言語化して伏線回収。
得られた最終形を示す。Solutions P104と一致している。

同ページHintには
Hd・He…1・3予約
Ae・Be…7・8予約
Bf・Cf…3・5予約
Dh・Eh…1・3予約
9…Ha・Hc→Cb・Eb・Fb…1・3・9予約
と書いてあった。
1行目と、なぜか4行目は2枚目(7枚上)のスクリーンショットに反映済みである。2行目は3枚目(6枚上)、3行目は5枚目(4枚上)のスクショに対応している。
5行目すなわち最終行は7枚目(2枚上)だが、前半はニコリさん呼称「いずれにしても理論」を表記するときの書き方だ!『超激辛』シリーズ巻頭の「解くときの考え方」には2の2の3解法に関する説明はないが、H列に着目すると9が入るのはHaとHcだけだから「いずれにしても」と考えることもできるのか、なるほど。
これも自ブログに記録を残したかった理由である。
ただし同行後半のCb・Eb・Fb…1・3・9予約を導くにはこれだけでは不足で、6枚目3枚上の2の2の3も必要である。これもまたいずれにしても理論で表現するとしたら、私だったら最終行は
9…Gh・Gi、Ha・Hc→Cb・Eb・Fb…1・3・9予約
あるいは
9…Gh・Gi→9…Ha・Hc→Cb・Eb・Fb…1・3・9予約
とでも書きたいところだが、わかりにくいかな?
久しぶりに他人には通じなさそうな喩えをやりたくなった。ラスボスに対して手持ちの必殺技がどれも通用しないというパターンはよくあるが、視聴者にはなじみのある地味めの能力を連続使用してラスボス攻略したというと『シン・ウルトラマン』のゼットン戦を思い出す。ネタバレかな?
ただしゼットンはウルトラマンシリーズ不動のラスボスの一人(?)だが、この問題はまだ91問中10問目にすぎない点が大いに違った。
むしろウェルカムである。難問もっと来い!
