自己満足的数独(ナンプレ)のプレイ記録である。タネ本ニコリさん『超激辛数独5』に突入したときは、のんびりゆっくり進めようと思っていたが、記録に残したい問題が次々に登場して、結果、更新頻度が多めになっている。前回はこちら。
『超激辛』シリーズ2大解法の「N連井桁」と「N国同盟/隠れ同盟」につき、後者についてN国同盟が成立するとき必ず9-N国以下の隠れ同盟が成立しているため、Nまたは9-Nの最大値は4を超えない旨は、たびたび書いてきた。
「N連井桁」に関して、行方向と列方向に井桁が共存している場合には、やはり小さい方は4を超えない。行方向がN連井桁であれば、列方向は9-N連以下となるからだ。
しかし、井桁が併存しない場合は、この限りではない。ただしこの場合、井桁に関与していないマスは値がただちに確定する。弊ブログでは冗談まじりに「1✕1仮想井桁」とローカル呼称している。量子力学でいう仮想粒子が、安定して存在できないことを踏まえている。量子力学理論なんて、これっぽっちも理解していないことは黙っていよう。
数独(ナンプレ)先進国である英語圏では、井桁に次のような別称をつけているそうだ。弊ブログでは再掲であるが、引用元サイトは今チェックしたらリンク切れになってしまっていた。
2✕2:X-wing
3✕3:Swordfish(メカジキ)
4✕4:Jellyfish(クラゲ)
5✕5:Squirmbag(もぞもぞ動く虫?)
6✕6:Whale(クジラ)
7✕7:Leviathan(レヴィアタン:海中の怪物・悪魔)
序盤でそのスクワームバグ法登場か? すなわち5連井桁と1✕1仮想井桁が登場したのかと思われた問題に突き当たった。『超激辛数独5』P22 15。難易度はLevel10に突入している。作者 アラームじ さん。初期値を背景色黄色で示す。
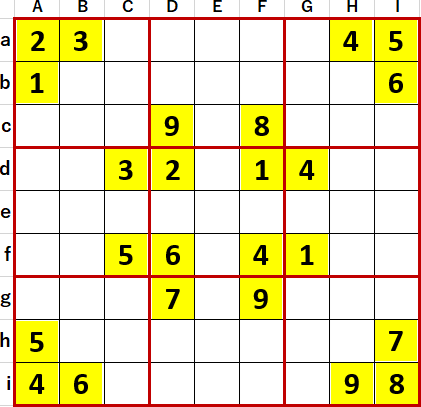
初等解法で埋められるマスは埋め、埋められないマスは候補として入りうる数字のメモ書きを書き尽くそうとしている途中で、次のような状態が出現した。
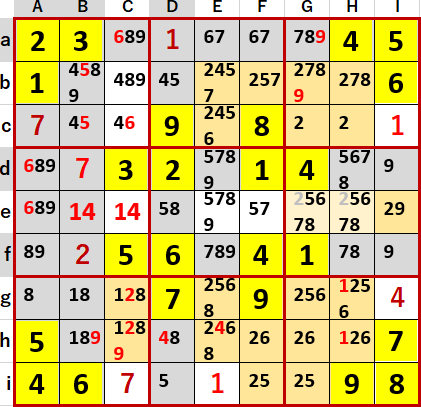
2について、(CEFGH・bcghi)の行方向5連井桁が成立している!
併存する列方向井桁は、Ieのみの1×1仮想井桁である。よってIeに2が確定する。
ただし右側3×3ブロックにおいて上段右側3×3ブロックと下段右側3×3ブロックで候補に2が存在するのはG列とH列だけだから、ローカル呼称「2の2の3」解法の適用と考えてIeに2が確定すると解釈することもできる。
あとから気づいたのだが、I列で候補に2が入りうるのはIeだけじゃないか! ローカル呼称「一気通貫」で初等解法も初等解法、キホンのキであった。
このように、結論は同じだけど結論を導くのに複数の理屈があてはめられるケースって、よくあるんだよな。
弊ブログはアフィリエイト広告を利用しています
以下、普通に解いてみた。候補として入りうる数字をすべてメモ書きし尽くした状態が、次のスクリーンショット。
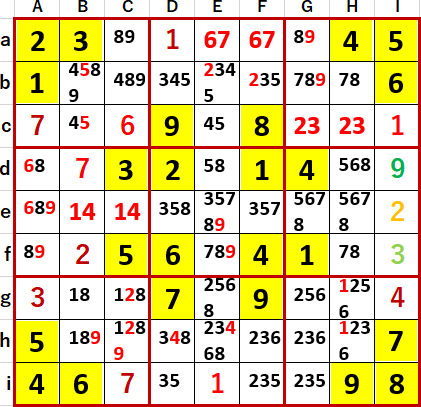
H列Hb・Hfの7・8 2国同盟は、すぐに見つかった。
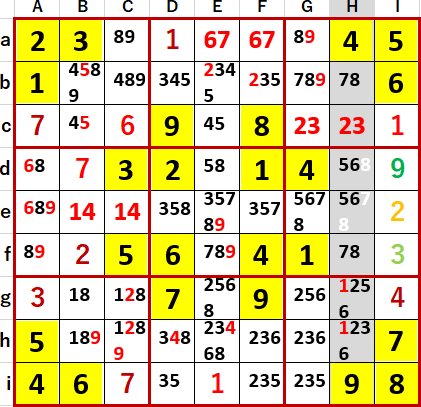
これを受けてH列と中段右側3×3ブロックには、Hd・He 5・6 2国同盟が成立した。
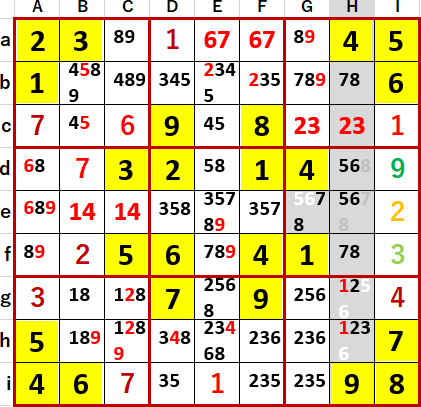
なおH列の1・2・3は隠れ隠れ3国同盟ないし2重隠れ3国同盟ということになる。ただし多重隠れ同盟は3重(隠れ隠れ隠れ)までが可能のはずだが、こちらにはあまり興味をそそられない。もしあったとしても、簡単に見つかってしまいそうだからだ。
話を戻して、g行Eg・Ggに5・6 隠れ2国同盟が…
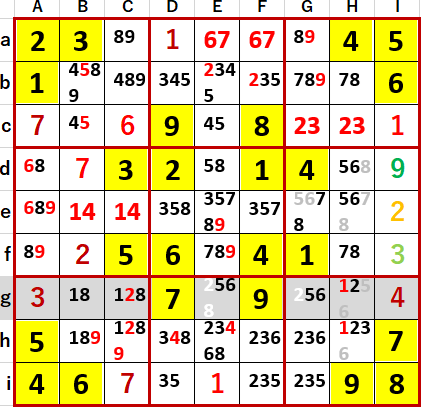
さらにh行Dh・Ehに4・8 2国同盟が見つかった。
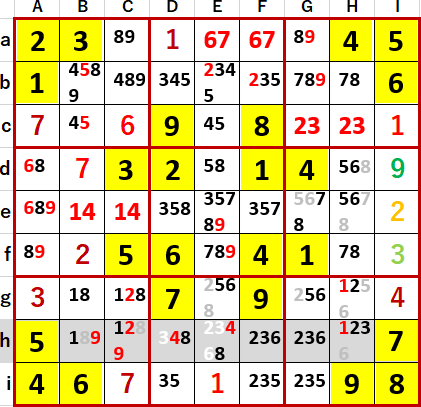
すると2の候補は、下段中央3×3ブロック中のF列Fh・Fiにしか残らない。
よって「いずれにしても」理論により上段中央3×3ブロックではF列Fbの候補から2が消え、Ebに2が確定した。
これをきっかけに多重選択の連続的解消が始まった。得られた最終形を示す。Solutions P105と一致している。
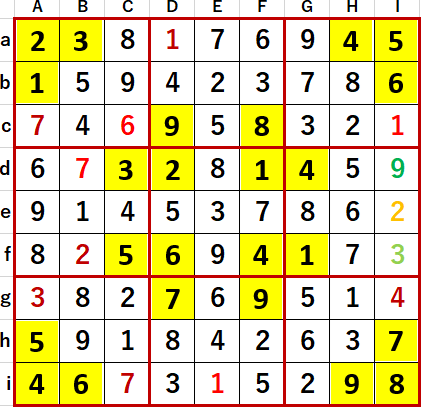
同ページヒントには
Ea・Fa…6・7予約
Bc・Ec…4・5予約
Ga・Gb・Ge…7・8・9予約
Eg・Gg…5・6予約
Dh・Eh…4・8予約
と書いてあった。予想していたことだが、5連井桁への言及はなかった。そりゃそうか。
1~2行目は,、3枚目(6枚上)のスクショに反映済みである。
3行目は5枚目(4枚上)のスクショに、4行目は6枚目(3枚上)のスクショに、5行目は7枚目(2枚上)のスクショにそれぞれ対応している。
5連井桁すなわちスクワームバグ法を使わなきゃ解けない問題に出くわすことは、今後の楽しみにとっておこう。
追記:
それからあれこれ検討したが、5連以上の井桁と1✕1仮想井桁の併存となる場合、1✕1仮想井桁を構成するマスは、必ず一気通貫でも確定できなきゃならないのか。
もし同じ行または列の2つ以上のマスに候補があれば、それらは2連以上の井桁を構成する。もし井桁を構成しなければ、同一行または同一列に同じ数字が2つ以上確定することになり、数独のルールに違反する。
