自己満足的数独(ナンプレ)プレイ記録である。前回はこちら。
今回の拙記事のブログタイトルは、わざと先月のこの記事のタイトルに似せた。
先月の記事は初期状態から初等解法で埋められる空白マスが一つもなかったという意味でつけたが、今回は初期値に特定の数字が一つも現れないことを意味したつもりだ。
ただし難度は決して高い方ではなかった。
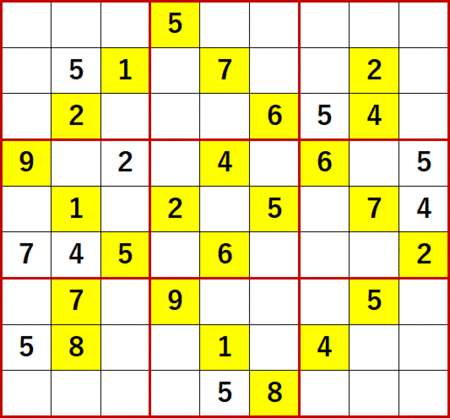
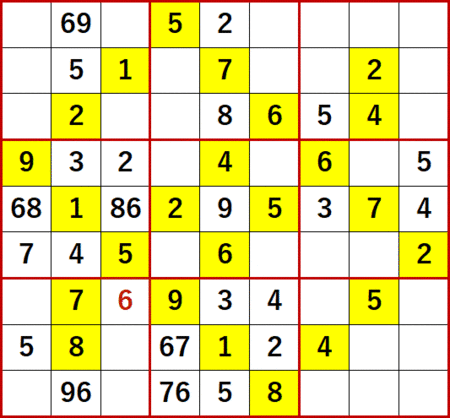
今回解いたのは ニコリ編著『ポケット数独上級篇1』P47 40 である。例によって初期状態を背景色黄色で示し、初等解法で埋められるだけの空白マスを埋めた状態からスタートする。
ご覧の通り 3 がどこにもない。
しかし一般的に初期値に登場数の少ない数字を埋めるのは苦労するものだが、この問題に限っては 3 をあぶり出すのにさほど困難は感じなかった。
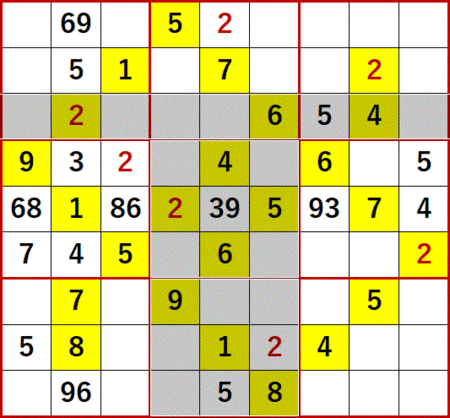
左側中段3×3ブロックに着目すると、上から4行目左から2列目には 6 と 8 が入れられない。従って次図のように 6 と 8 の二国同盟が成立する。
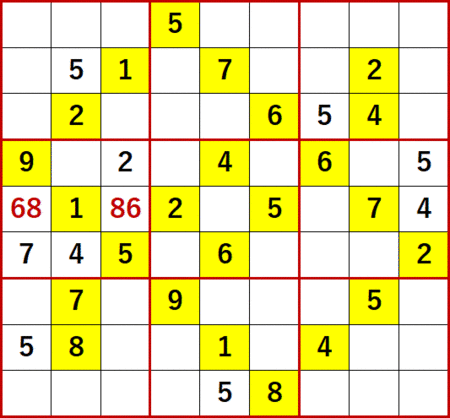
よって左側中段3×3ブロックの残る1つの空白マスに、早々と 3 が確定したのである。
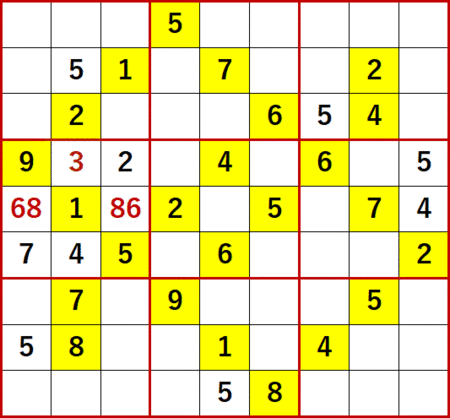
またこれにより左から2列目と上から5行目(下から5行目)に、次図のように2国同盟が成立する。
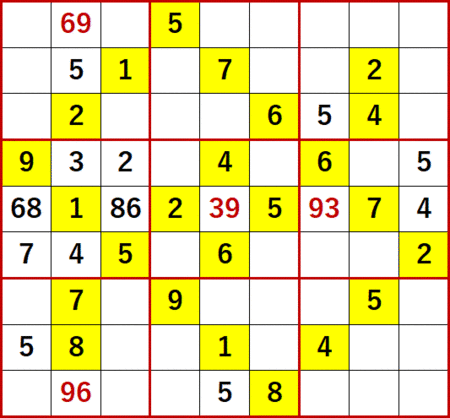
つぎに 2 に着目すると、下から2行目には 2 の入るべき空白マスが1つしか残っていない。弊ブログのローカル呼称で「一気通貫」と呼んでいる初等テクニックである。

続いて左から5列目(右から5列目でもある)に着目すると、やはり一気通貫で 2 の入るべき空白マスがいちばん上の行にしか残っていないことがわかる。
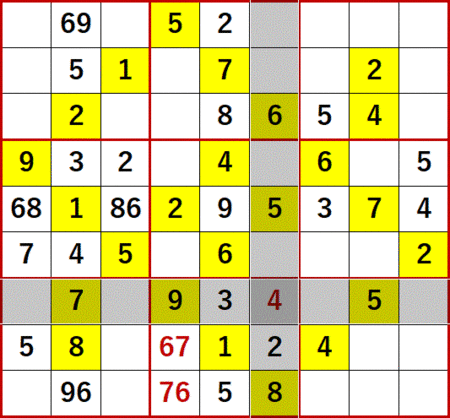
ここでローカル呼称「総消去法」を用いる。左から5列目、下から3行目に着目すると…
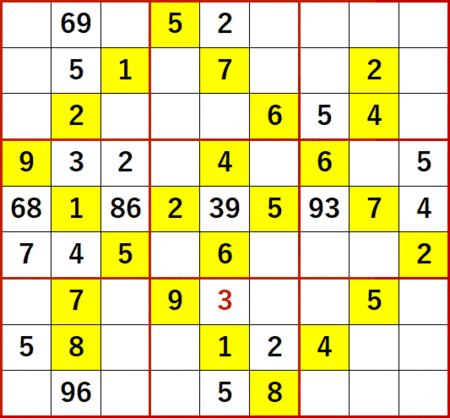
1 は同一3×3ブロックにある。
2 は同一3×3ブロックおよび同一列にある。
4 は同一列にある。
5 は同一行および同一列にある。
6、7 は同一列にある。
8、9 は同一3×3ブロックにある。
…ということで、またまた 3 が出てきた。
この 3 が確定したことにより、左から5列目の残り1つの空白マスには 8 が確定する。また上から5行目の 3 と 9 の2国同盟が解消される。もはや 3 には難敵という印象はない。舐めたらあとでよく痛い目見るけど。
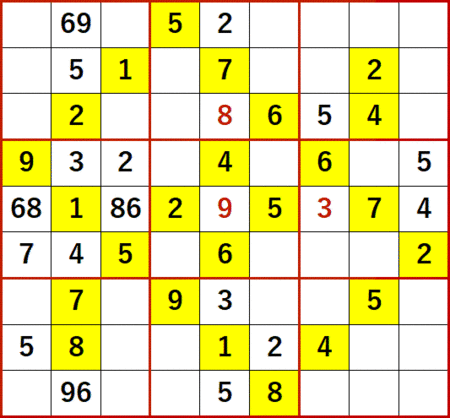
ともあれ下段中央の3×3ブロックブロックに着目すると、下から3行目右から4列目には 6 と 7 が入れられないから、次図のように 6 と 7 の2国同盟が成立する。よって同3×3ブロック最後の空白マスである下から3行目右から4列目に 4 が確定する。
次に下から3行目、左から3列目に対し総消去法をもう一度適用する。
1 と 2 は同一列にある。
3 と 4 は同一行にある。
5 は同3×3ブロックおよび同一列にある。
7 は同一行にある(同一3×3ブロックでもある)。
8 は同一3×3ブロックにある。
9 は同一行にある。
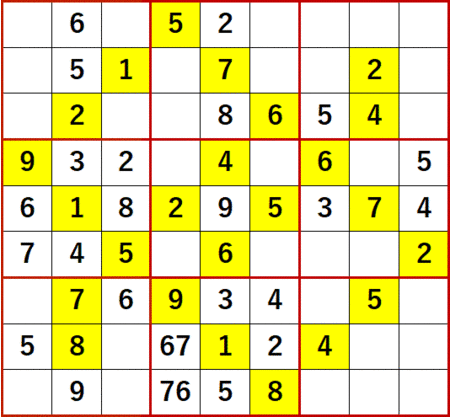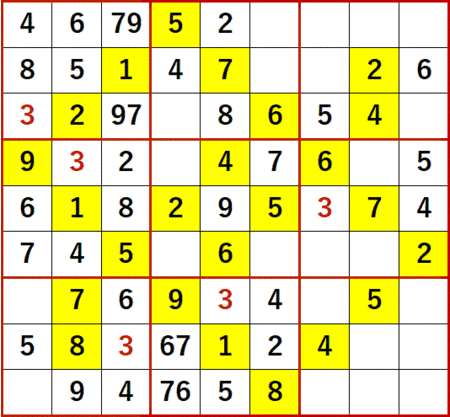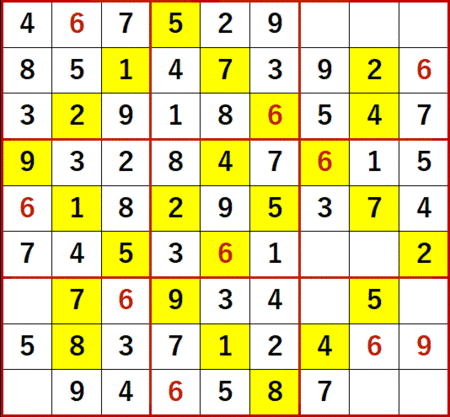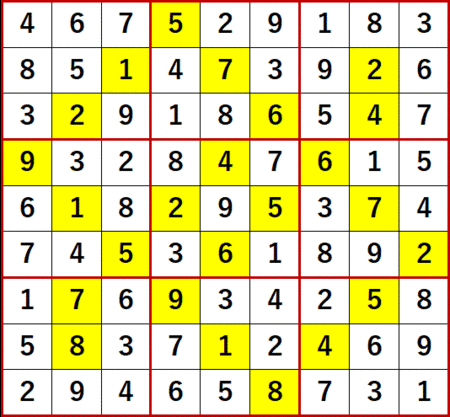
…ということで 6 が確定する。
この 6 によって、上から5行目と左から2列目の2国同盟が解消された。

これだけ手がかりがあれば十分だろう。以下、最終形まで初等解法のみで行きつけた。
その様子を gifアニメ で示す。
いつもの通り最終形のみ静止画で示す。ANSWERS P118 と一致している。
前回(10/18付)同様、すべての空白マスを候補の数字で埋め尽くさなくて済んだ。
実は最初に解いたときには全部のマスを候補で埋めたんだけど、それをやっている過程で総消去法が適用できるマスがいくつかあることに気づき、ブログに公開するにあたって最終形までの道順を再構成した。
最初に解いたときの手順とブログに公開した手順が違うのは、いつものことである。