数独(ナンプレ)の自己満足的プレイ記録である。前回はこちら。
タネ本・ニコリ編著『ポケット数独 上級篇』(ソフトバンク クリエイティブ) は「数独の解き方」と題された短いまえがき以外は文章がなくて、1ページあたり1問、巻末に解答という体裁であるが、問題を順に解いていくと明らかにポリシーがあると感じられる。
だがそれを文章で他人に通じるように説明することは、きわめて困難だとも感じる。そういうことは、例えば受験問題集を順に解いていくと編集者の意図がわかるとか、いろんな局面で存在するのだろうが。
しかし「実際に解いた者にしかわからない」と言ってしまうのはあまりにも簡単なので、問題の配列に隠された編集意図をなんとか少しでも他人に伝えられないかというのが、弊ブログの一連の記事に込められた薄い目的でもある。
基本的には「せっかく解いたのにすぐに忘れちゃうのがもったいないから」というのが主動機なのだが。
今回もgifアニメは1枚だけで、あとは静止画ばかりである。
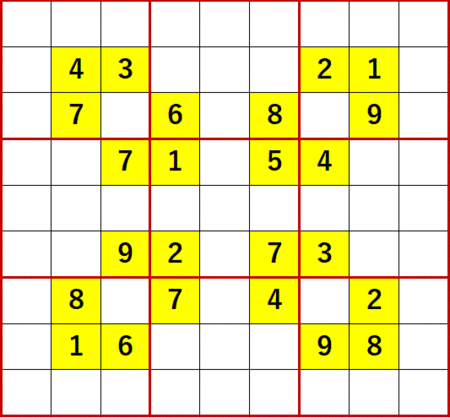
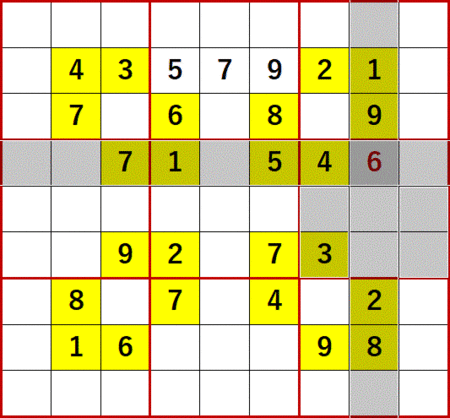
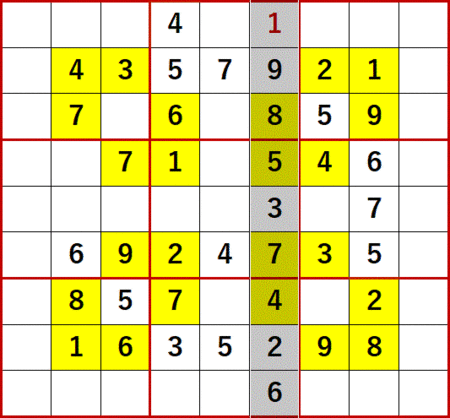
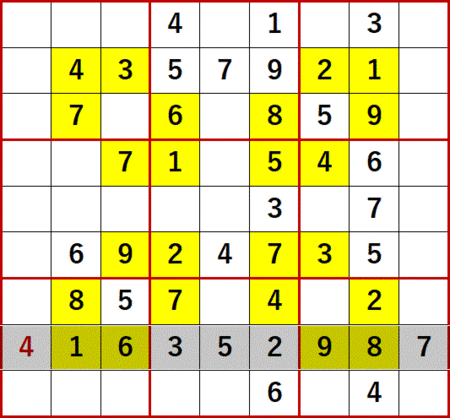
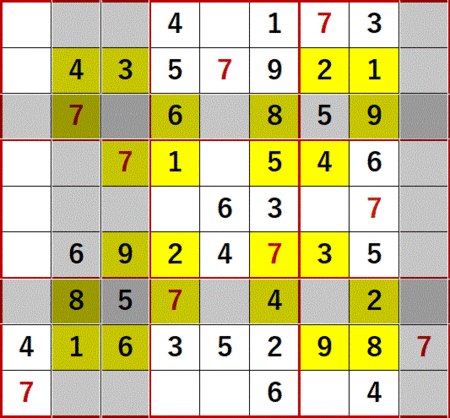
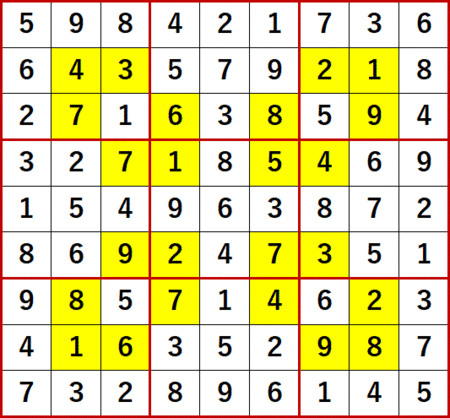
今回ネタにする上掲書P25 18(Level7)は、そろそろこんな問題が出てくるんじゃないかと思っていた、まさにそんな問題だった。初期値を背景色黄色で示す。
いつもなら「飛車にらみ」「一気通貫」「どっちに入ってもこっちしか残ってないだろう」とローカル呼称している初歩的解法で埋められるだけの空白マスを埋めた状態からスタートしているが、この問題に関してはこれらの解法では1マスも埋められなかった。
そろそろこんな問題が出てくるんじゃないかと言ったのは、そういうことである。
望むところよ! ならば「総消去法」を使うか? それとも「二国同盟」か?
総消去法の出番だった。
総消去法というのはやはり弊ブログのローカル呼称で、特定の空白マスに特定の数字以外のどの数字も入らないことにより入る数字を決定する解法である。
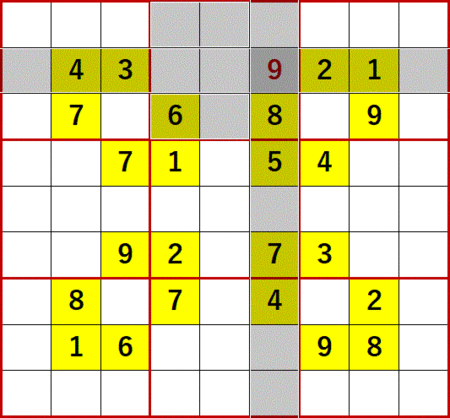
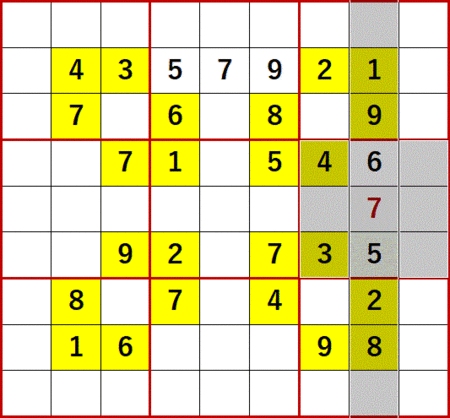
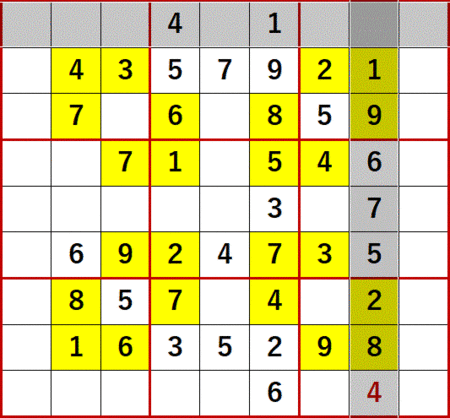
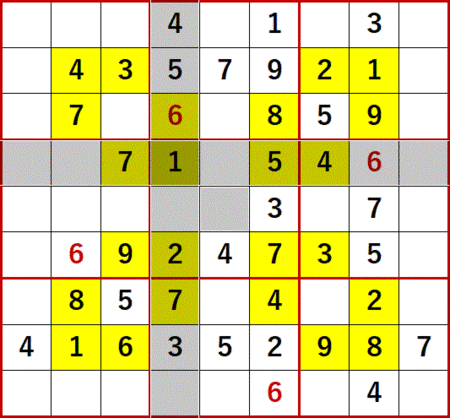
まずは上から2行目、右から4列目の空白マスに着目する。
1、2、3、4 は上から2行目にある。
5、7 は右から4列目にある。
6、8 は同じ3×3ブロック中にある。
よって上から2行目、右から4列目の空白セルに入る数字は9に特定できる。
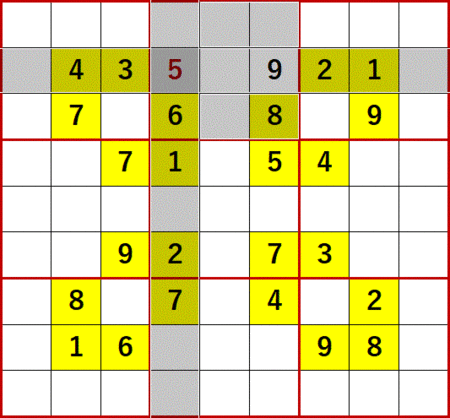
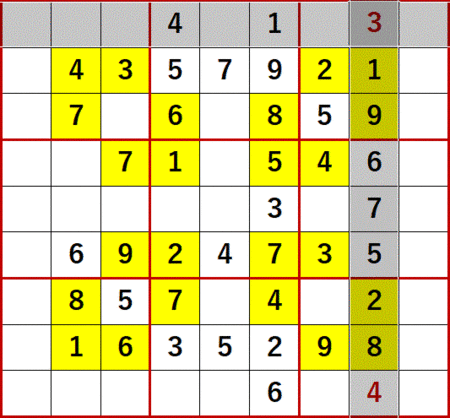
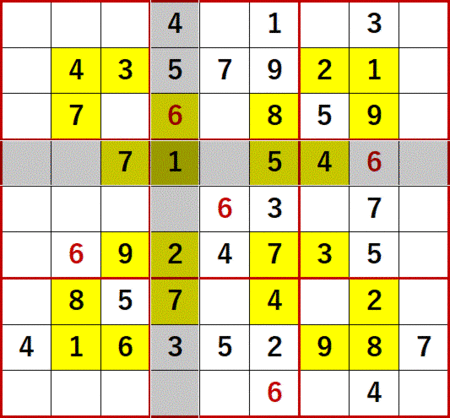
この9が決まると、上から2行目、右から4行目の空白マスにも総消去法が適用可能になる。
1、2、3、4 は上から2行目にある(1、2は左から4列目にもある)。
6、7 は左から4列目にある。
8、9 は同じ3×3ブロック中にある(9は上から2行目にあるとも言える)。
よって上から2行目、左から4列目は5に特定できる。
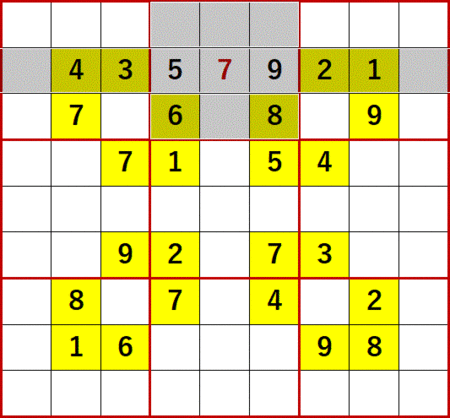
9と5を利用すると、上から2行目、右から5列目(左から5列目でもある)は7に特定できる。説明は省略する。
次に上から4行目、右から2行目の空白マスに着目する。
1、2、8、9 は右から2列目にある。
3、4 は同じ3×3ブロック中にある。
5、7 は上から4行目にある。
よって上から4行目、右から2列目は6に特定できる。
右から2列目は5、7が順次確定するが、説明は省略する。
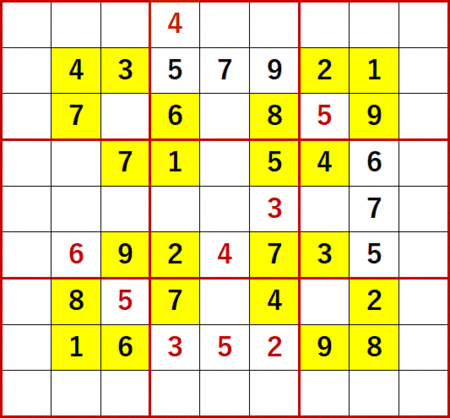
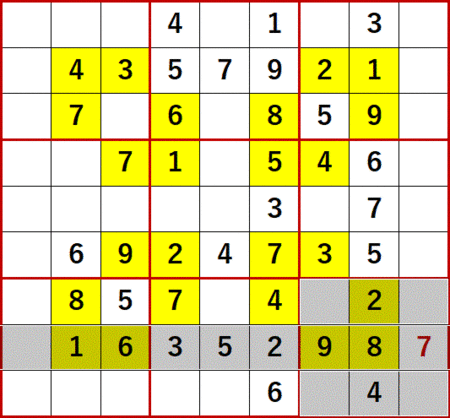
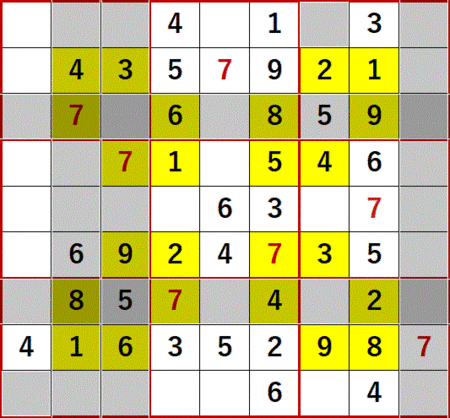
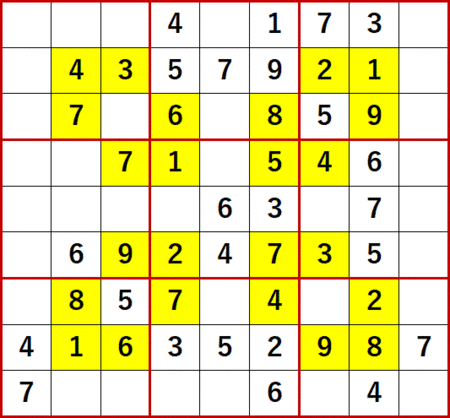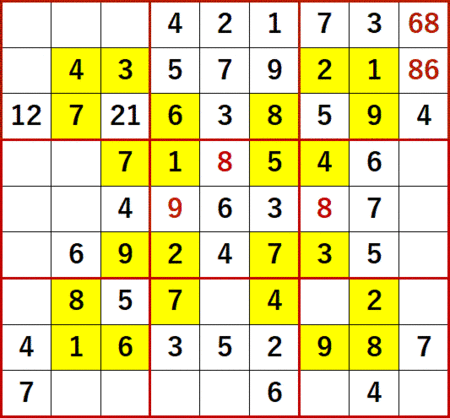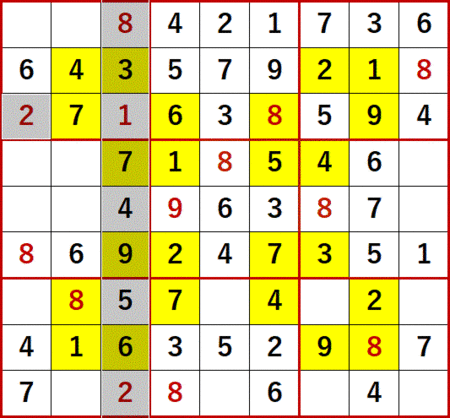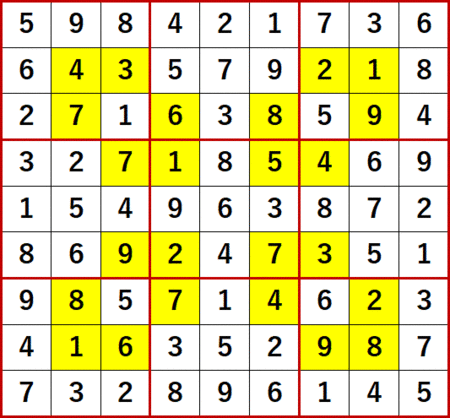
総消去法を用いて埋められるだけの空白マスを埋めた状態が、次図である。
初期状態において初期値のあるマスと空白マスの配置は上下、左右で対称だったが、埋められるマスも対称とは限らない。
ここから他の解法も使用する。
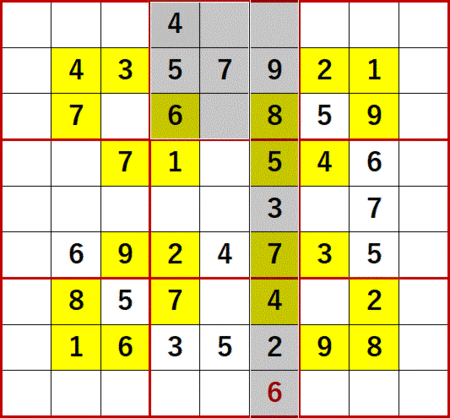
右から4列目には最上行と最下行に空白マスが残っているが、同列で未使用の数字のうち6は上段中央3×3ブロック中に存在するので最上行には入れられない。
同列最上行の空白マスには1が確定する。
このように1列または1行に着目して数字を決定する解法を、弊ブログでは「一気通貫」とローカル呼称している。
次に右から2列目に着目すると、最上行の空白マスには4が入らないから最下行に4を入れるしかない。
すると最上行の空白マスに、残った3が確定する。これも一気通貫である。
あとで考えたら、最上行の3を総消去法で決定することもできた。あとになって気がつくことが、よくある。
ともあれ、右から2列目最下行の4が確定したことにより、総消去法で下から2行目の右端列に7を確定することができるようになった。
下から2行目の左端列には4が確定する。
今度は6の飛車にらみを用いて、中段中央3×3ブロック中の6を確定する。
特定の数字(この場合6)の同じ行と同じ列に同じ数字が入れられないことを利用した解法を、弊ブログでは飛車にらみとローカル呼称している。
同様に7の飛車にらみを用いて、上段右側3×3ブロック中と下段左側3×3ブロック中の空白マスに、それぞれ7を確定する。
以降、最後まで解いているところをgifアニメで示す。最初のほうで「二国同盟」と呼ばれる解法を用いているが、そんなに難解ではないはず。
いつものように最後に完成図を示す。『ポケット数独上級篇1』ANSWERS P116と一致している。
スポンサーリンク