数独(ナンプレ)の自己満足的プレイ記録である。前回はこちら。
今回のニコリ編著『ポケット数独 上級篇』(ソフトバンク クリエイティブ) P22の15(Level7)は、これまでは主に単独で使用していた解法テクニックの複合技を、序盤で多く使ったことが特徴的に感じたのでブログに記録する。
今回もgifアニメは1枚だけで、あとは静止画ばかりである。
目次
「どっちに入ってもこっちしか残ってないだろう」解法の連鎖使用
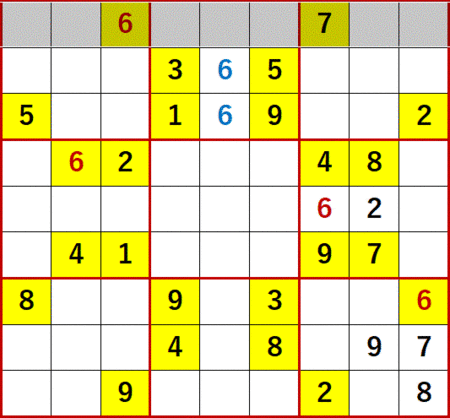
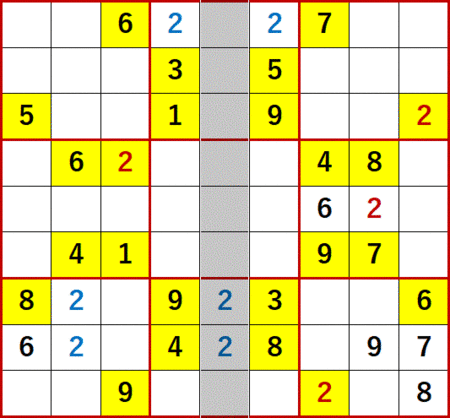
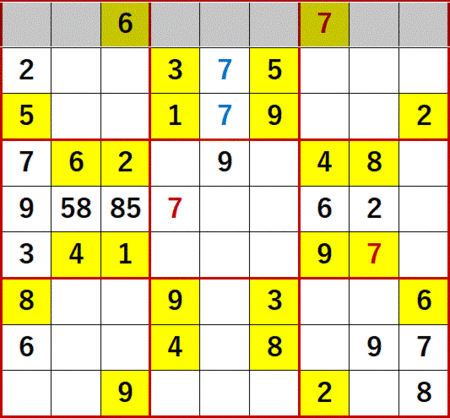
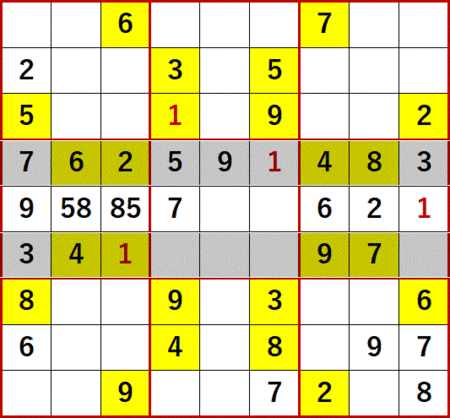
初期値を背景色黄色で示し、ローカル呼称「飛車にらみ」で機械的に埋められる空白マスを埋めた状態が下図である。
この問題で特徴的なのは、空白マスがT字状に残った3×3ブロックが4つもあることである。
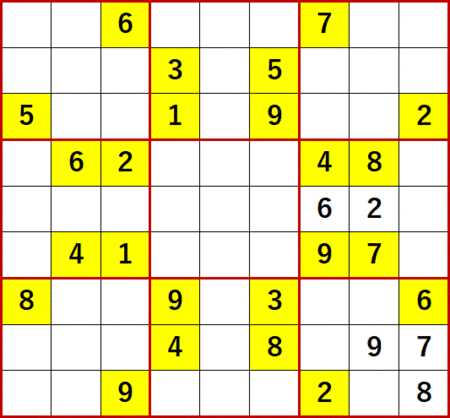
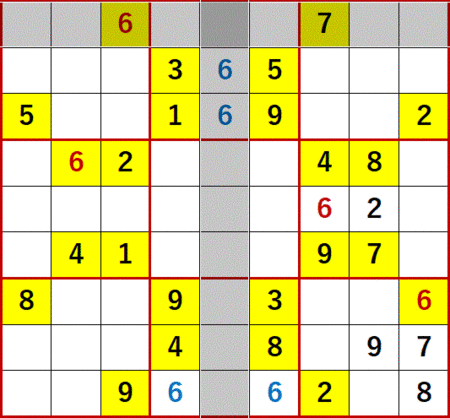
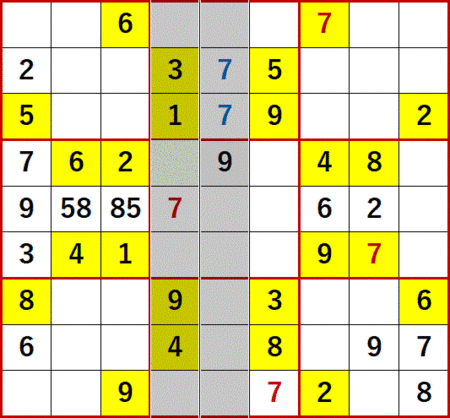
まず6に着目する。上段中央3×3ブロック中で6が入れられるのは、左隣3×3ブロック中1行目の6の飛車にらみにより、次図中に青文字で示す2つだけである。
特定の数字が入れられる空白マスが同一3×3ブロック中で縦または横に並んでいる場合、並んでいる縦方向または横方向に飛車にらみを効かすことができる。この解法を弊ブログでは「どっちに入ってもこっちしか残ってないだろう」と呼んでいる。
上段中央3×3ブロック中6の飛車にらみをたどると、下段中央3×3ブロックで6を入れられる空白マスは、最下行にやはり青文字で示した2つしかないことがわかる。
これらの6についても、横方向の飛車にらみを利用することができる。
上段左側の6、中段左側の6と組み合わせて、下段左側の6を特定することができる。
いまのどこが珍しかったかというと、ローカル呼称「どっちに入ってもこっちしか残ってないだろう」解法を連鎖使用つかカスケード使用しても有効ということだ。
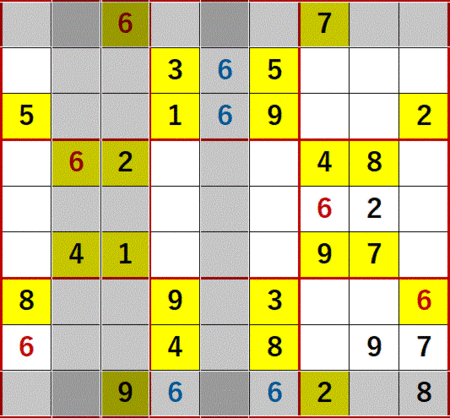
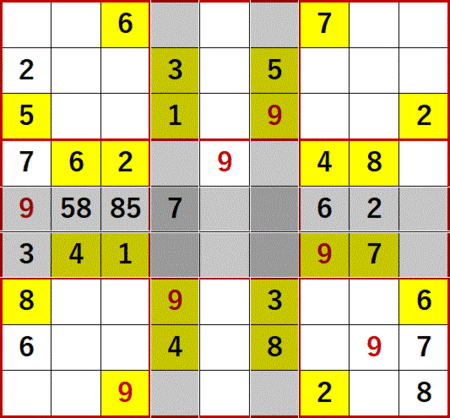
似たことが2に着目したときも利用できる。下段右側3×3ブロック最下行2の飛車にらみにより下段左側3×3ブロックと下段中央3×3ブロックに2を入れられる可能性のある空白セルが、次図に示すようにそれぞれ縦に2つずつ並んでいることがわかる。
うち下段中央3×3ブロック2の飛車にらみをたどると、上段中央3×3ブロックで2が入る空白セルは次図に青文字で示す1行目の2つしかないことがわかる。
これらを使用して、上段左側の2を特定することができる。
二国同盟を利用したローカル呼称「総消去法」
数独の解法の名称としての「二国同盟」は、純正(?)二国同盟、裏二国同盟、隠れ二国同盟など使い分けているサイトもあるようだが、うちの場合あまり区別しないで使っている。すなわち空白セルに入れられる数字が2択に特定されれば、二国同盟と呼んでいる。
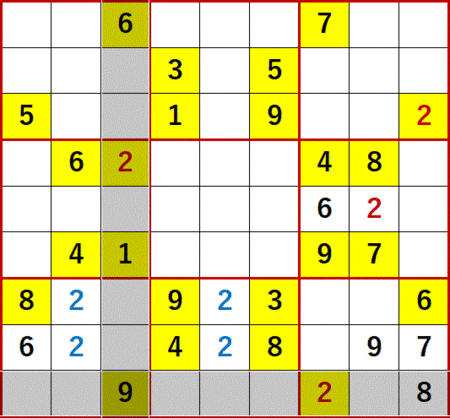
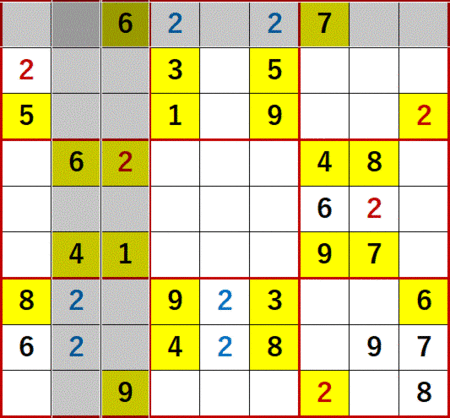
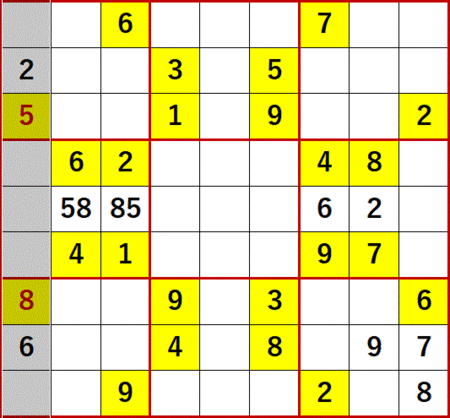
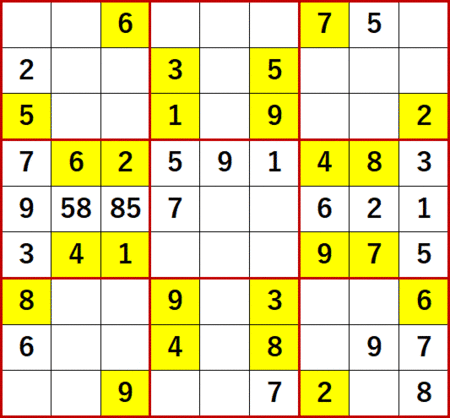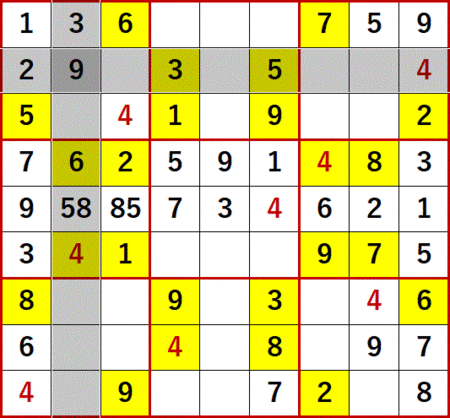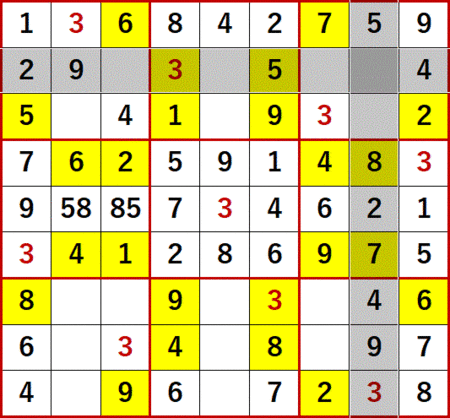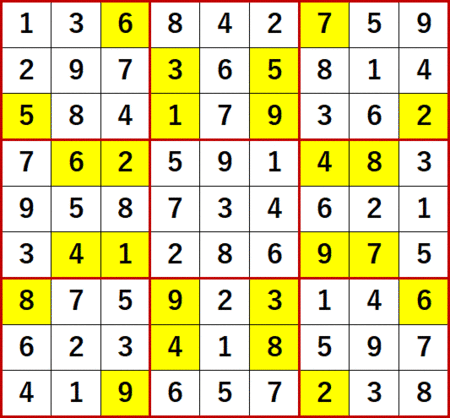
左端の列に着目すると上段左側3×3ブロックに5が、下段左側3×3ブロックに8があるため、中段左側3×3ブロックの左端列以外にある2つの空白セルには5か8しか入らないことがわかる。次図中にはそれを58、85で示した。
続いて下から4行目に着目すると右側中段3×3ブロックに7と9があるので、左側中段3×3ブロックの下から4行目以外の空白セルには7か9しか入らないことがわかる。次図中にはそれを79、97で示した。
そうすると、同3×3ブロックに最後に残ったセルに3が確定する。
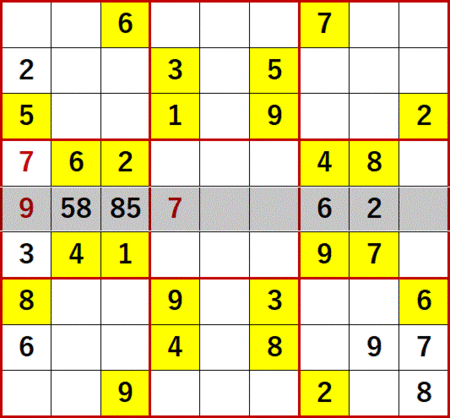
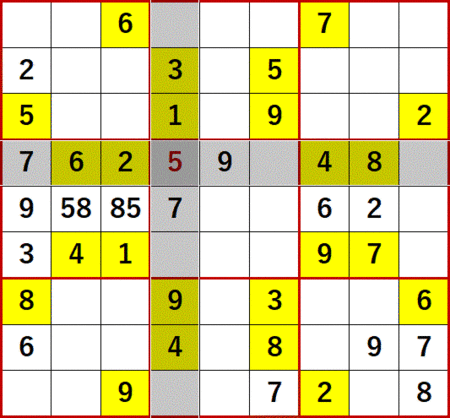
上から(下からでもある)5行目、左から4列目の空白セルに着目する。
1は、左から4列目にある。
2は、上から5行目にある。
3は、左から4列目にある。
4も、左から4列目にある。
5と8は(どちらがどちらに入ったとしても)上から5行目にある。
6は、上から5行目にある。
9は、左から4列目にある。
よって、上から5行目、左から4列目の空白セルに入る数字は7に特定できる。
特定の空白セルに入る数字を消去法によって1つに特定する解法を、弊ブログでは総消去法と呼称している。
今のどこが珍しかったかというと、二国同盟と総消去法の組み合わせは、弊ブログでは初登場である。
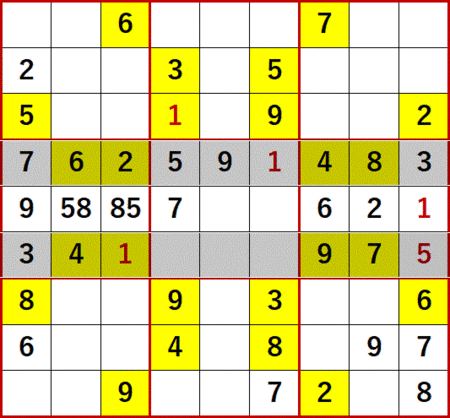
この7によって、中段左側3×3ブロックの7と9の二国同盟が、次図のように解消される。
1行目の7により上段中央の空白セルに入る7が2つしかないことは、初期値の状態で判明していたことだが…
総消去法により左から4行目の7が決定したことで、下段中央の7の特定に活用できるようになった。
また二国同盟の解消により決定した9とその他の9たちの飛車にらみによって、上から4行目、右から(左からでもある)5行目の9を決定することができた。
この9によって、上から4行目、左から4列目の空白セルにも総消去法が適用可能になった。
1は、左から4列目にある。
2は、上から4行目にある。
3は、左から4列目にある。
4も、左から4列目にある。
6は、上から4行目にある。
8も、上から4行目にある。
9は、上から4行目 *と左から4列目* にある。
よって、上から4行目、左から4列目の空白セルに入る数字は5に特定できる。
追記:
9はもともと左から4列目にあったので、前段の9が確定しなくても総消去法は適用可能でした。あとで気がつくことがよくあります。失礼しました。
追記おわり
一瀉千里
以降は、基本的な解法だけで最後まで行けるのではないだろうか。
上から4行目の空白セルは残り2つだが、右から4列目にはすでに3があるから、3は右端の列にしか入らない。
上から4行目に最後に残った右から4列目の空白セルは、1で特定される。
行または列に着目して数字を特定する解法を、弊ブログでは「一気通貫」とローカル呼称している。
新たに定まった1を利用した飛車にらみで、上から5行目最右列の1が決定し…
中段右側3×3ブロックに最後に残った空白セルには5が定まる。
以降はラストまでgifアニメで示す。のっけに3の「どっちに入ってもこっちしか残ってないだろう」が出てくるくらいで、あとは飛車にらみと一気通貫くらいしか使用していないはず。総消去法も二国同盟も、もう出てこない。
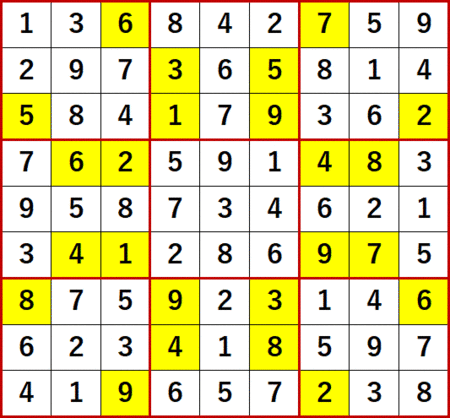
いつもの通り完成図を示す。ANSWERS P115と一致している。
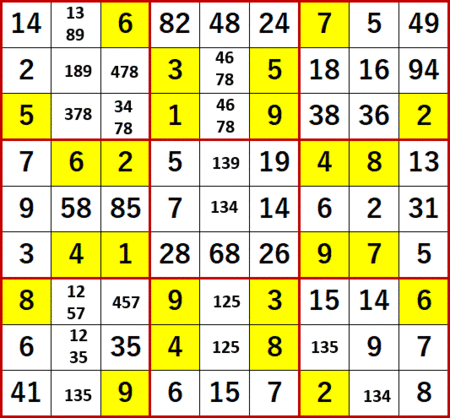
念のために書いておくが、ブログにまとめたものは他人にもできる限りわかりやすくするつもりで後から整理したストーリーであって、最初に解いているときは候補を埋めながらやっているのでぐじゃぐじゃである。
こんな調子で。このまま他人に見せたって、何をやっているかわかるわけがない。しかも後から「もっといい解法があった!」と思いつくことがよくあるので、二転三転するし。
思うに人生のエピソードも、そんなものかも知れない。日常は意味の取りにくい千変万化に満ち満ちているが、それを他人に説明するため、あるいは自分自身で理解するため、枝葉細目をバッサリ斬り落としてわかりやすいストーリーに再構築することの繰り返し…とまで言うと話の拡げ過ぎか?
スポンサーリンク