自己満足的数独(ナンプレ)のプレイ記録である。タネ本『超激辛数独1』はその後「裏二国同盟」ないし「裏三国同盟」、または「X-Wing」で解ける問題が続いている…という旨は前回2月22日付拙エントリーにも書いたな。
今回のエントリーの結論を先に書いてしまうと、P47 40(Level10) を解くにあたって新技を開発する必要が生じたのかな、と思ったが、これは裏四国同盟という既知の技であることに気づいたということである。
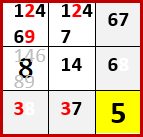
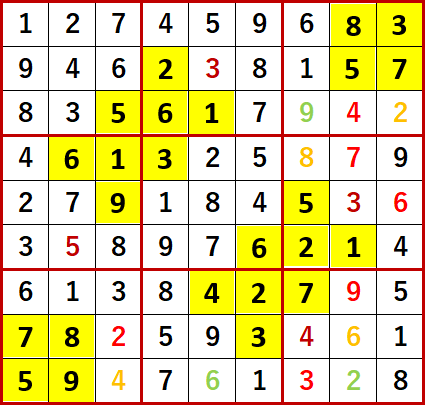
作者は printf さん。初期状態を背景色黄色で示す。
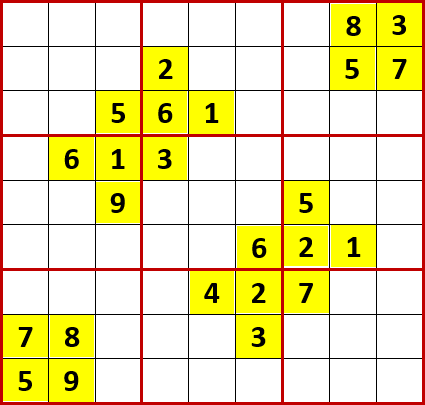
わが解法アルゴリズム「二択先書き法・改」により埋められる空白マスを埋め、埋められない空白マスには候補の数字メモを書き尽した状態が下図。初等解法により埋められた数字については、決定した順にExcelカラーパレットの左から順にフォント色を与えている。各3×3ブロックで入れられる空白マスが2択となる数字は、フォント色を赤にして他の候補の数字と区別している。
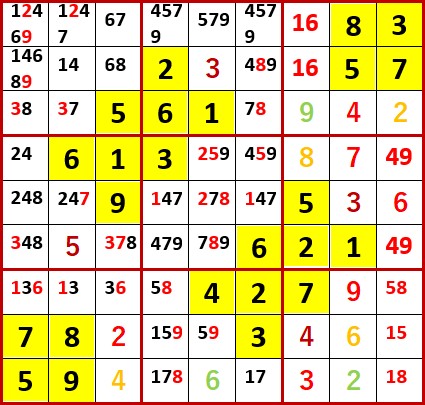
この状態で前述の裏二国同盟、裏三国同盟、X-Wing、それに他に私の使えるY-Wingやローカル呼称「2の2の3」などの解法テクニックで適用できるものがないか検討したが、見つからなかった。
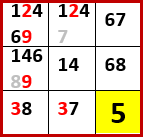
何か手掛かりはないかと探し、特徴的だと感じたのが左側上段3×3ブロックである。
このブロックだけをトリミングして再掲する。
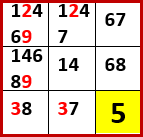
左から3列目と上から3行目の空白マスがどれも2択で、行と列にそれぞれ7と8が1つずつ含まれている。
これ、もし3行目、3列目以外の空白マスに7を入れたら、3行目、3列目の4つの空白マスに入れられる数字が3、6、8の3つしかなくなるので不足する!
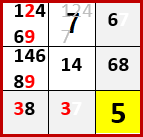
同様にもし3行目、3列目以外の空白マスに8を入れたら、3行目、3列目の4つの空白マスに入れられる数字が3、6、7の3つしかなくなるので不足する!
すなわち左側上段3×3ブロックで3行目、3列目以外の空白マスの候補から、7と8を除外できるじゃないか!
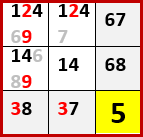
このパターンは、レアケースではあろうが初出のはずだと思った。2択を利用する点ではY-Wingと似ているが、Y-Wingとは明らかに違っている。
何かローカル名称を与えるとしたら、X-Wing、Y-Wingに続いてZ-Wingというところか? いや元ネタの「スター・ウォーズ」シリーズにZ-Wingという戦闘機は出てこなかったようだから、同シリーズに登場するV-Wingなんて形状的にもいいんじゃないか…
などと気の早いことを頭の一部で考えていたが、左側上段3×3ブロックの候補から7と8を一つずつ除外しただけでは、事態がぜんぜん進展しないことも判明した。
これだけやって、ようやく気づいた。これ1、2、4、9の裏4国同盟だったのだ!
すなわち3行目、3列目の4つの空白マスに入る数字の候補は3、6、7、8の4つに限定される。
いっぽう3行目、3列目以外の4つの空白マスに入る数字の候補の1、2、4、9の4つは、同ブロック中のそれ以外の空白マスには入れられない。
結論として、同ブロック3行目と3列目以外の空白マスに入る数字の候補からは、7と8だけじゃなく6も除外できたのだった!
先ほどの7と8に関する検討は、裏4国同盟により候補の絞り込みが可能であることの(部分的な)再検証に他ならなかった。いわゆる「車輪の再発見」というやつだ。
同様の検討を6に対しても行うことにより、6も候補から除外できることがわかる。
裏4国同盟は、初出ではなかったよな?(誰に訊く?
とまれ、これでようやく多重選択の連鎖的解消が始まった。
最左列で6が入るのは下から3行目しか残っていない。ローカル呼称「一気通貫」である。
下段左側3×3ブロックでは下から3行目に1、3、6の3国同盟が成立していた。
最左列に6が確定したことにより、3列目の3と2列目の1が確定した。
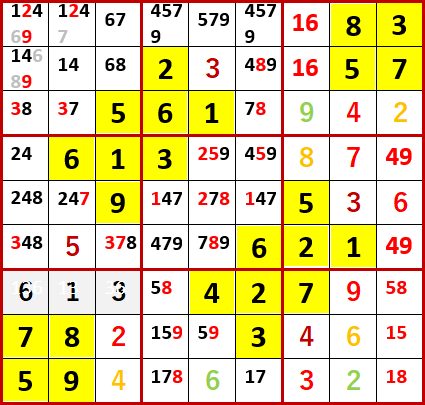
下から3行目左から2列目の1は、上から2行目の4を確定する。
また下から3行目左から3行目の3は、下から4行目の2択の3の片割れを消すので、残りの3が最左列下から4行目に確定する。
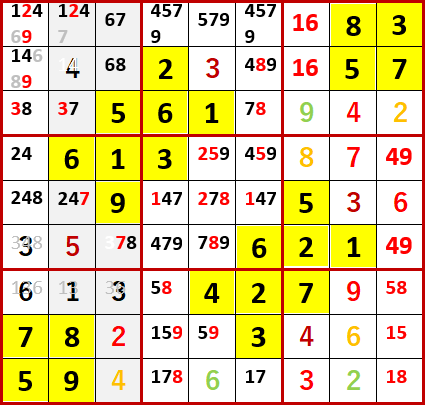
この3が、上段左側3×3ブロックの3、6、7、8の4国同盟の解消を導くのである。
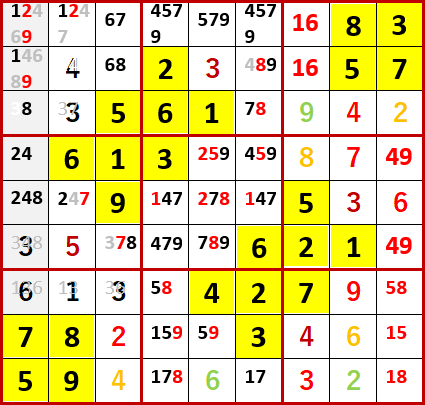
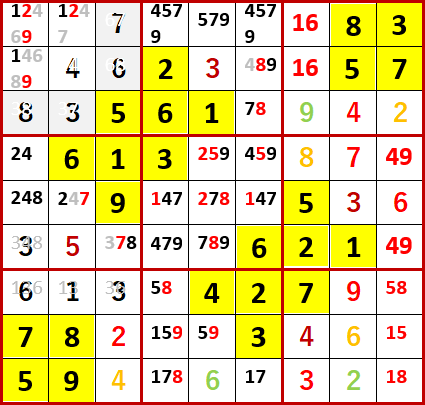
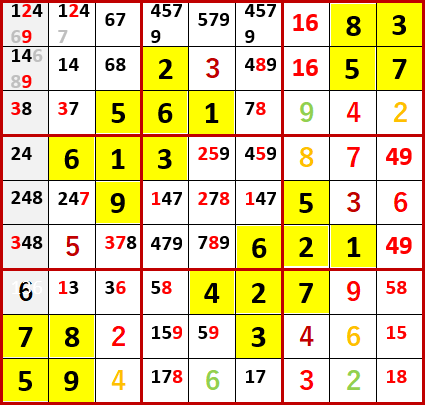
最終形を示す。Solutions P111と一致している。
同ページのヒントには
Dg・Ig…5・8予約
Aa・Ab・Ba・Bb…1・2・4・9予約
と書いてあった。
2行目は、弊ブログの言葉に直すと「最左列と左から2列目、最上行と上から2行目に1、2、4、9の裏4国同盟が成立している」ということに他ならない。
1行目は、下から3行目の最右列と左から4列目に5と8の2国同盟が成立しているということである。この情報は、今回2枚目に示した候補の数字を埋めた図を作るにあたって、すでに利用させてもらっていた。
スポンサーリンク

