自己満足的数独(ナンプレ)プレイ記録エントリーの3連投になってしまった。
前回拙記事には、早々とヒントを見てしまった後悔とともに、今後ふたたび新技「裏3国同盟」を使う局面が出てきたとき適切に対応できる自信がないと書いた。
実際にはその後すぐ「裏3国同盟」ないし「4国同盟」を使って解いた問題があった。ほっ。ただしその問題は「裏3国同盟」or「4国同盟」を使わなくても解けることが判明したので、ブログネタにはしづらかった。
今回取り上げるのはニコリ『超激辛数独1』P24の17。作者は鴻上和也さん。難度はLevel9、9+、10、10+の4段階中9+を超えて10に突入していた。初期値を背景色黄色で示す。
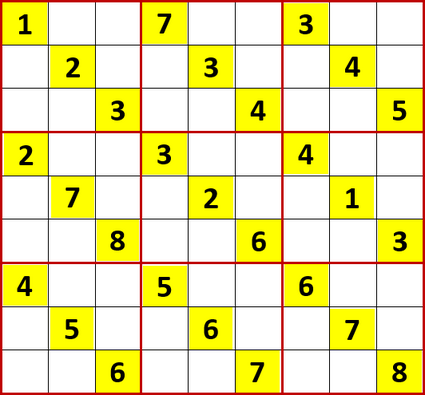
ちなみにLevel9+(問10~16、P17~23)は初期値の数がずっと少なく、相変わらず自分自身のミスを最大の強敵として戦ったが新技を使うことなく解けた。
この問題に至って再び初期値の数が増えたので、作者さんになんらかの意図があるなとプンプン匂った。
まず気づいた特徴は、X-Wingの連続使用だった。
経験上、初期値に現れる数字の数が多いものから初等的に埋められるマスを潰していくと、空白マスにメモする数字の候補の数を減らせる。数字の候補のメモ書きは、数が少ない方がミスを犯しにくい。
3の初期値が5つもあったので、ローカル呼称「飛車にらみ」にて埋められるマスを埋め…
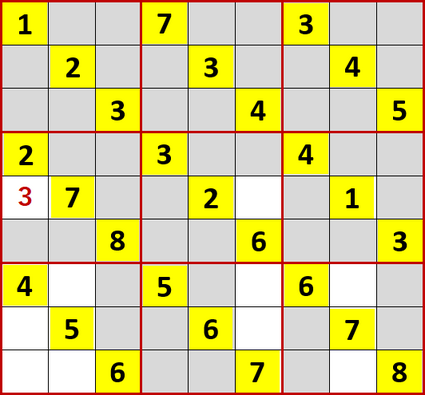
各3×3ブロック中で入れられる空白マスが2択になる場合は、フォント色赤でメモ書きした。
さっそく左から2列目と右から2列目、最下行と下から2行目にX-Wingが成立しているのを見つけた。ニコリさんの呼称では「井桁」である。
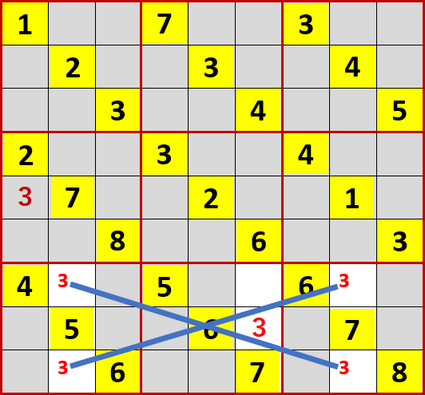
これにより右から4列目、下から3行目の空白マスには3が入れられないことがわかる(もし入れたら、右から2列目か左から2列目で3を入れられるマスに不足が出る)。
よって右から4列目下から2行目の3が確定した。
後から思考過程がトレースできるよう、Excelカラーパレット左から順にフォント色を変えている。
続いて6。やはり初期値の数が4つと多かった。
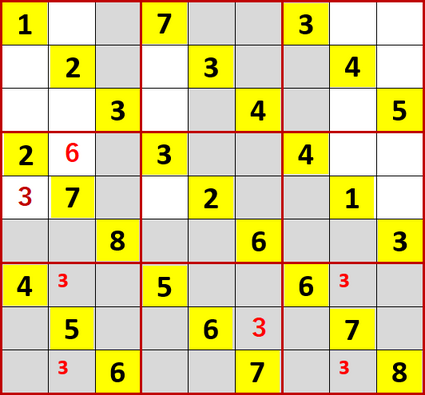
左から2列目上から4行目の6の確定に伴い、最右列上から5行目(下から5行目でもある)の6が確定するとともに、最左列と左から4列目、上から2行目と3行目にX-Wingが成立した。これらは最上行右から2列目の6を確定した(最右列および上から2行目と3行目には6が入れられない
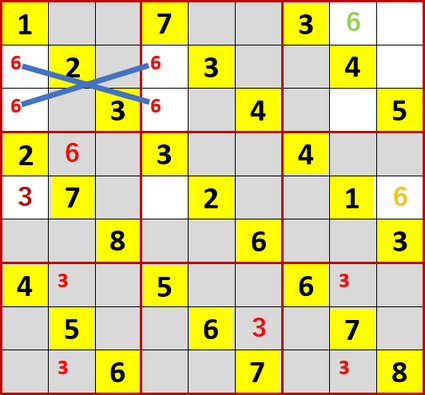
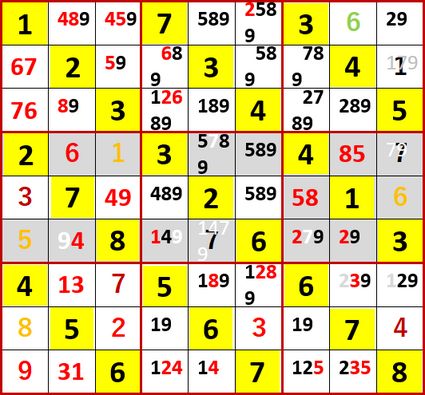
そんなでローカル呼称「2択先書き法・改」にて埋められるマスを埋め埋められないマスには候補の数字を書き尽したのが、次図である。
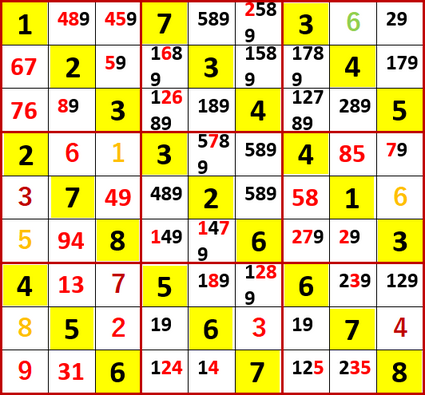
この状態で目を皿にして精査したところ、最上行と下から3行目、最右列と右から4列目の2が、X-Wingを構成しているのを見つけた。見つけるのが遅れたのは、これらの2のうちすべてが2択(フォント色赤)ではなかったからだ。
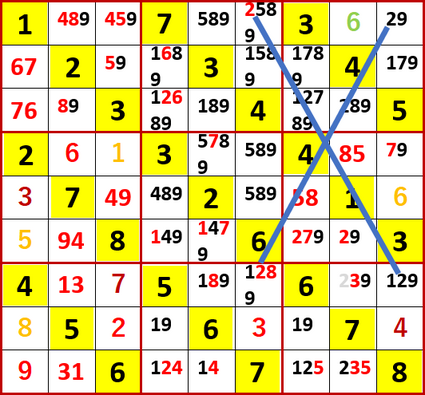
このX-Wingは右から2行目、下から3列目の空白マスに入る候補から2を消したが、それ以上の進展を与えてはくれなかった。
長考の果て、Y-Wingを発見した!
左から2列目下から3行目の1と3、右から2列目下から3行目の3と9、右から3列目下から2行目の1と9である。

右から2列目下から3行目の3と9に着目する。もしこのマスに3を入れたら、左から2列目下から3行目は1が確定する。このとき下から3行目の他の空白マスには1が入れられなくなる。

もし同じマスに9を入れたら、左から3列目下から2行目には1が確定する。そうすると下段左側3×3ブロック中の他の空白マスには、1が入れられなくなる。

どっちにしても、右側下段3×3ブロック中の下から3行目の空白マスには、1を入れることができないことが判明する。
なおもし左側下段3×3ブロック中に空白マスが残っている場合、Y-Wingはそれらの中からもいくつかの候補を除くことができるが、今回の場合同3×3ブロックはすべてのマスが確定済みなので適用外である。
その説明は、以前も貼ったけどこちらのサイトの「3. パターン2」をご覧ください。ただしこちらでの呼称はXY-Wingとなっています。
話を戻して、この問題の場合は右から3列目下から3行目は6が確定済みだったので、最右列下から3行目の空白マスに入る数字の候補から1を除外できただけだが…
ローカル呼称「一気通貫」により、最右列上から2行目の1が確定した!

さらにこの結果を受けて、上から4行目の7が確定し…
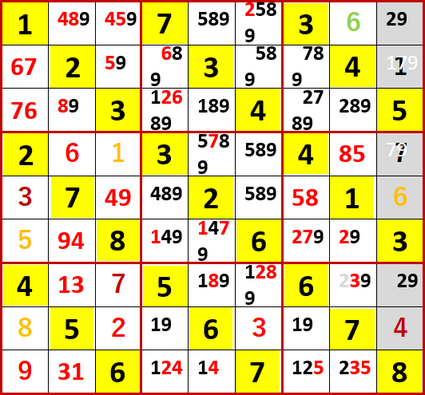
この7をきっかけに、多重選択の連鎖的解消が始まった。
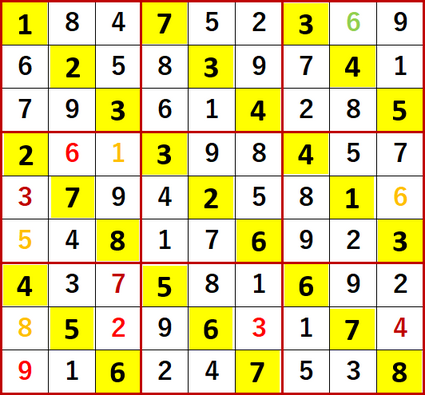
最終形を示す。Solutions P106と一致している。
ときに同ページのヒントには、何と書いてあったかというと…
Fb・Fg・Ib・Ig…1井桁
とのことで、うちのブログの呼称に直すと「最右列と右から4列目、上から2行目と下から3行目にX-Wingが成立している」となる。
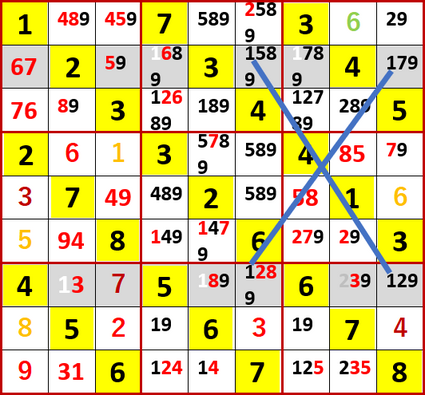
ええっ、本当だ!
しかも、いきなり多重選択の解消が始まってしまいそう。
つまりY-Wingを使わなくても解けたってことか!
まあいいのだ。X-Wingだって、弊ブログ過去記事では「X-Wingを使わなくても解けたけどX-Wingと言いかったからX-Wingを使ったと、何度となく言ってきたではないか!
今回も、Y-Wingと言いたいからY-Wingと言っているまでである。

