自己満足的数独(ナンプレ)ネタの連投です。昨日付(2/7)エントリーに『超激辛数独1』には解答編にヒントがついているが、できるだけ見ないようにしようと決意したと書いた。
早々に食言してヒントを見てしまったというのが、今回の本題です (^_^;
前振りとして、連携機能でツイッターに流した前回エントリーに、FFさんから次のようなリプを頂きました。ありがとうございました。
最初の四国同盟は見方を変えると裏二国同盟ですね。たぶんヒントはそのことでしょう。
ポイントとなる6枚目の画像を再掲します。
なるほど確かに上から2行目左から2列目と右から2列目に入る候補のうち、5と7は他のマスの候補には含まれていません。ということは、これらのマスのどちらかに5と7以外の数字を入れると、上から2行目に5と7のどちらかを入れるマスが不足を来すことになります。これは2国同盟、ニコリさんの呼称による「予約」に他なりません。
よくある2国同盟と区別するため「裏2国同盟」あるいは「隠れた2国同盟(ヒドンペア)」という呼称を用いるサイトがあることは、うろ覚えの記憶がありましたが、自分で意識して使ったことはありませんでした。
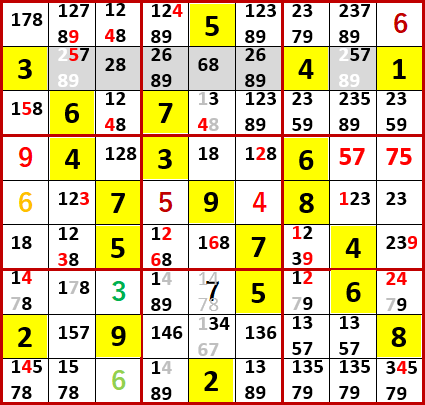
これを踏まえて、今回取り上げる問題はP14 7(Level9)、いつもの通り初期値を背景色黄色で示す。
ローカル呼称「2択先書き法・改」にて空白マスに入る数字を埋め尽したのが、次図。

早くもここで手が止まった。にっちもさっちも行かない感あった。
これまでだったら、ここで何晩か寝かすところである。だがくどいようだが『超激辛』にはヒントがある。ついふらふらと、P103のヒントを見てしまった。
Ge・Gg・Gi…2・4・5予約
うちのブログの呼称に直すと、「右から3列目の下から1、3、5行目に2、4、5の3国同盟がある」ってこと?
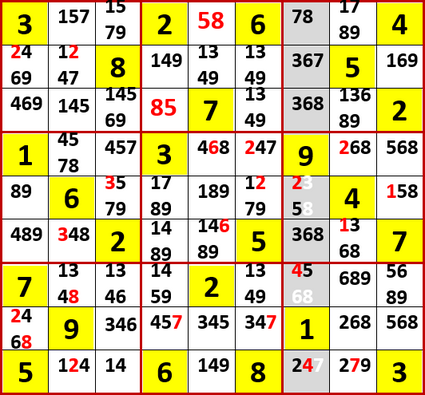
ええっ、これは「裏3国同盟」!?
すなわち2、4、5の3つの数字は、これらの3つの空白マス以外に入れられるマスの候補がない。ということは、これらのマスに2、4、5以外の数字を入れると、右から3行目に2、4、5を入れるマスが不足することになる。だからこれらのマスに入る数字の候補から2、4、5以外の数字を除外することができるのだ!
こんなの1年寝かせても、自力で思いつく自信はない。
一方でこれまで新技を開発した記憶に照らすと、どうして思いつけたか自分でもわからなかったし、どれだけ時間をかけたら思いつくことができたかを予測することも不可能だった。また新技を思いついたときの高揚は、何物にも代えがたいものがある。
一言で言うと、とても悔しいぞ!
もう一つ、これからも「裏2国同盟」「裏3国同盟」は、繰り返し出てくる可能性がある。その時に適切に対処できるか自信がない。
ともあれ最終形まで導かねば。
裏3国同盟が最下行右から3列目の7の二択の片割れを消すので、最下行右から2列目に7が確定する。
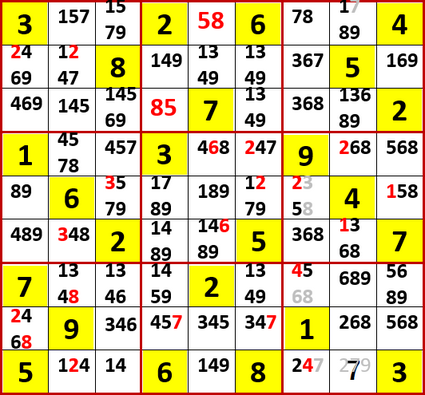
そうすると最下行に1、2、4の(裏でない)3国同盟が判明するので…
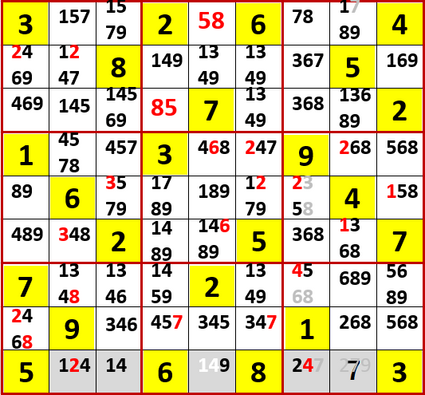
最下行右から5列目(左から5列目でもある)に9が確定する。
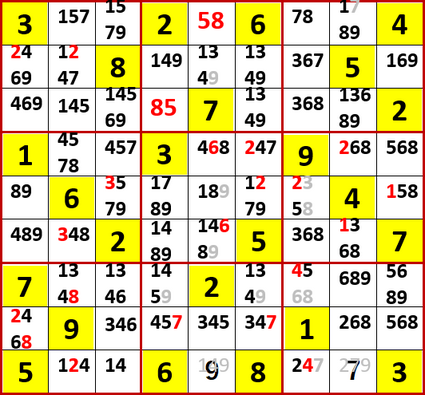
次に右側中段3×3ブロックに着目すると、右から3列目上から5行目(下から5行目でもある)の3が消えるため下から4行目に3の半確定ライン(ニコリさんの呼称「いずれにしても理論」)が成立する。
よって左側中段3×3ブロック中の2択の3の片割れが消え、左から3列目上から5行目(下から5行目でもある)の3が確定する。
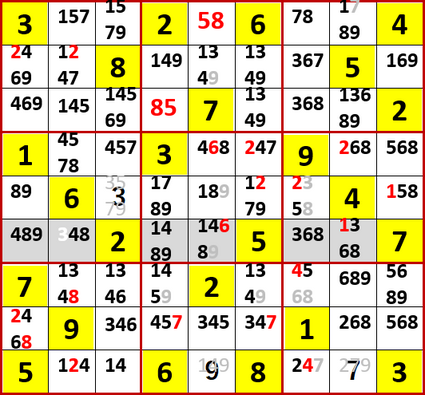
さらに左から2列目では、ローカル呼称「一気通貫」により下から3列目の3が確定する。この列では、他に3を入れられる空白マスがないのだ。

右側中段3×3ブロックでは4、8、9の(裏でない)3国同盟が判明するので、他のマスの候補から4、8、9が除外できる。
上から4行目に判明した5、7の2国同盟は、同行の候補を次々と消すのだが、このあたりでいいだろう。以下、連鎖的に多重選択の解消が始まる。
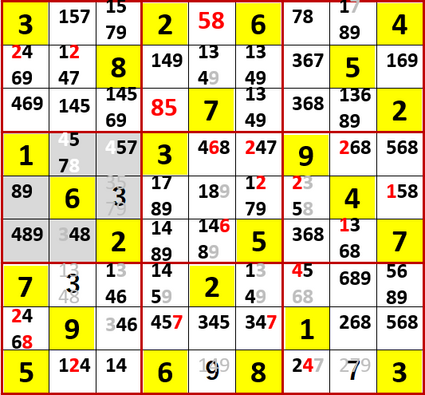
最終形を示す。Solutions P103と一致している。
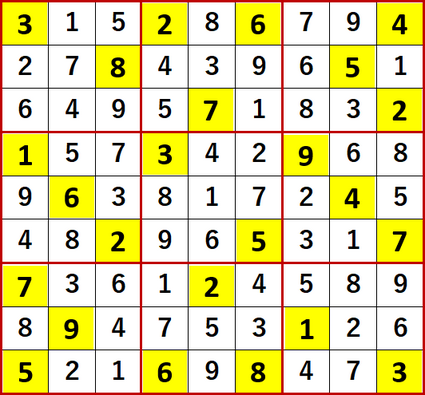
今回の裏3国同盟を新技にカウントすると、昨日の4国同盟(裏2国同盟と考えても結果は同じ)に続いて早くも新技2つ目だ。
『超激辛』は91問中まだ1桁、難易度はLevel9、9+、10、10+中最弱の9である。最弱って何だよ?
この先どうなるのか、怖いような楽しみのような…