自己満足的数独のプレイ記録である。前回はこちら。
一時期はてなブログの「#数独」タグからの流入が増えて気づいたのだが、数独プレイ記録を再開したのが去年の7月だった。それからまだ丸1年も経っていないとは!
必要に迫られて次々と新解法を習得していったので、もっと時間が経っているものだと思っていた。ひょっとしたら、こういうことを「充実」と言うのかもしれない。おこがましいけど。
いっぽうで、もしその時間をたとえば専門書を読破するのに充てていたら、などとも考えないでもない。専門書に関しては「一年に一冊ずつ読破する習慣を身に着け、それを長く続けられたら…」と考えたことがあり、ちっとは実践した期間があった。だが少なくとも数独に再ハマリしてからは、そっちはお留守になっている。あかんやないか。
数独を専門書にカウントしてもいいですか?(誰に訊く?
今回はニコリ『超激辛数独1』コンプリートの報告である。終盤近くなって、同書の2大解法テクニック「予約」と「井桁」を連続使用しなければならない凝った問題が、続々登場した。P96の89、P97の90あたりも取り上げたいところであるが、今回はキリということで最後の問題であるP98の91をネタにする(特に89は、後日エントリーにするかも知れない)。
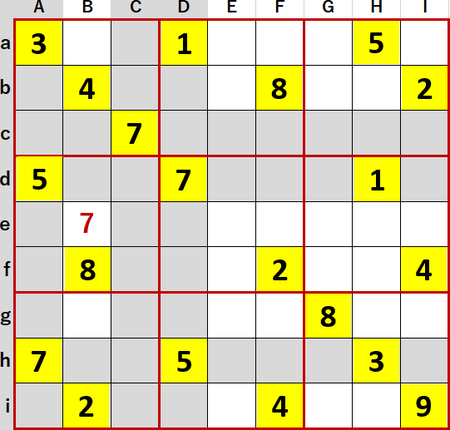
作者は 近藤夲 さん、難易度はLevel10+。いつもの通り初期値を背景色黄色で示す。
まずは初等解法により埋められるマスを埋め、埋められないマスには候補の数字をメモ書きするのだが、最終盤に至って「井桁」による候補の絞り込みも同時進行させることが必要になった。でないと候補のメモの分量が多くなりすぎ見通しが効かないのだ。
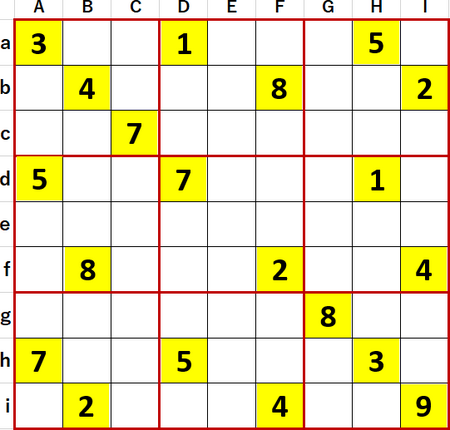
初期値の数が多い7から始めた。7が飛車にらみするマスを灰色で着色すると、Beに7が確定することがわかった。
Beの7の飛車にらみも着色すると、Fa・Ia・Fg・Igの列方向単純井桁(X-Wing)が判明した(背景色濃いめの橙)。ローカル呼称「井桁ケンカせずの法則」により行方向には(EGH・bfi)の3連井桁が成立していることを確認しつつ(背景色同じ)、両井桁により7が候補から除外できるEa、Ga、Eg、Hg(背景色薄い橙)以外の空白マスに7をメモ書きする。同一3×3ブロック中で2択となる候補は、重要情報につきフォント色を赤に変えている。
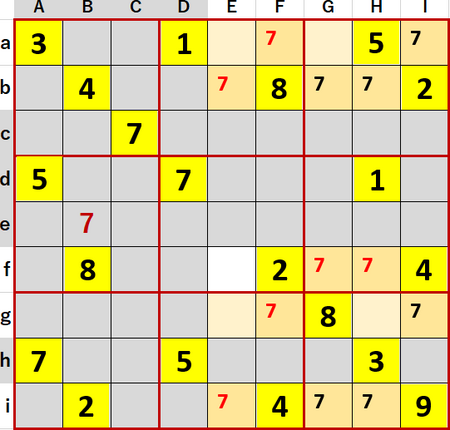
続いて8のチェックを行った。初等的に確定するマスはなかった一方、(CEI・ach)の行方向3連井桁ないし(ADH・cei)の列方向3連井桁が見つかった。井桁を構成するマスを濃いめの橙で、井桁により8が候補から除外されるマスを薄めの橙で着色し、候補8のメモを書き込んだ状態が次図である。
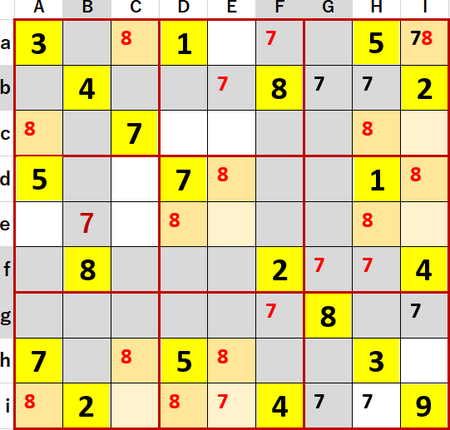
この問題で特徴的だったのは、2と4が(CEG・adh)の行方向3連井桁ないし(ADH・cgh)の列方向3連井桁という同じ井桁を構成していたことだ。2と4がB、F、Iという同一列上、b、f、iという同一行上に存在することに着目すると納得できる。
次図は2について同一3×3ブロック中で2択となる候補のメモを書いた後、4について同様の処理をしているところである。
2と4が同一3×3ブロック中で予約あるいは2国同盟を構成している場合は、これまた重要情報のため目立つようにフォントサイズを大きくしている。別の数字がそれらのマスの候補に入らないことを示すためである。
2国同盟は2と8、4と8についても見つかったので、同様の表示をしている。

それ以外の候補の数字も書き尽した状態が次図。5についても井桁が見つかったが、説明と図は省略する。いつもだったら初期値を示した次の図として示しているところだが、井桁による候補削減を同時進行させないと候補メモの数字が爆増する。

のみならずc行、e行、h行、C列、H列の2・4・8予約(3国同盟)が、ただちに判明する。これによりHc、Heから候補6、9、Ch、Ehから候補1、6、9を除外できる。
9は初期値1マス、6は初期値0マスと初期値の数が少ないので候補メモの数が多いが、前図による候補削減によりこの2つについても井桁チェックをしてみようという勇気が湧いた。
9からチェックすると、(BFG・adh)の行方向3連井桁ないし(ACDEH・bcefg)の列方向5連井桁が出現した!

この結果、c行の9の候補はEcだけになり確定した。ローカル呼称「一気通貫」である。
この9がいくつかの候補を消すことにより、Ceの9も確定した。やはりe列の9の候補が、ここにしか残らなかったためである。

しかし、これ以上の確定はできなかった。弊ブログでは「多重選択の連鎖的解消が始まらなかった」と形容している。
次に6の井桁チェックを行ったところ、(ACDH・bfgi)の列方向4連井桁ないし(BFGI・acdh)の行方向4連井桁が出現した!
4連井桁というのは、4国同盟ないし隠れ4国同盟と並んで本書においては最難関テクニックである。直前にやったように、併存する井桁を確認すると5連以上が見つかることはあるが。
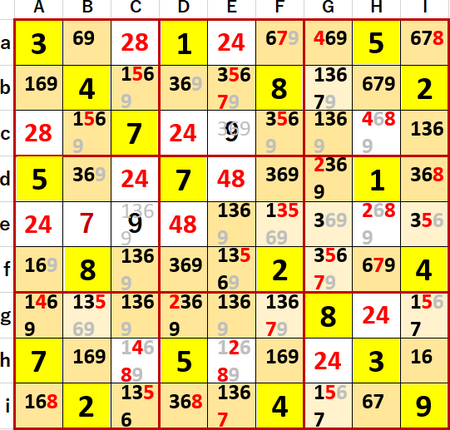
少し補足すると、数独は9×9の空間しかないので、井桁が併存する場合4連井桁が最大のはずである。それ以上の場合、併存する井桁の難易度が下がる。
同様にN国同盟の場合は、N国同盟に加入しなかった数字が隠れN-1国同盟を構成するので、やはり4国同盟ないし隠れ4国同盟が難易度最高である。
ただし井桁の場合は、9×9の空間上に単独の井桁しか残らない可能性がある。そういう場合において5連井桁以上が成立する可能性は残るように思うが、現実にそんな問題にはまだ出くわしたことがない。
とまれGeの候補から6が消え3が確定したことを手がかりに、多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P124と一致している。
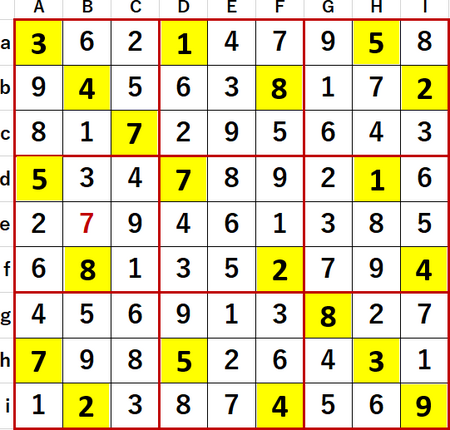
恒例となった同ページのヒントとの照合である。
(CEG・adh)…2・4井桁
(CEI・adh)…8井桁
c列e列(ADC)、C列E列
(adh)…2・4・8予約
(ADH・bfg)…9井桁
(ACDH・bfgi)…6井桁
いろいろと思うところはあるが、今は1点だけ。下から2行目の「(ADH・bfg)…9井桁」というのが、わからない。
3枚上の図中に残存する9の3連井桁というのであれば理解できるが、ヒントとしては4枚上の図の説明で述べた「(BFG・adh)…9井桁」のほうを書くべきではなかっただろうか?