前回「その3」の最後に書いた、重みW1、W2、バイアスb1、b2のグラフ描画用データを一括して採取するコード改造は、あっさりできた。
#コード4-0
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import *
from common.gradient import numerical_gradient as n_g
x_e = np.array([[0, 0], [1, 0], [0, 1], [1, 1]])
t_e = np.array([[1, 0], [0, 1], [0, 1], [1, 0]])
weight_init_std=50.
W1 = weight_init_std * np. array([
[ 0.07395519, -0.13489392, -0.1178099 ],
[ 0.01890785, -0.02397794, 0.18300705]])
W2 = weight_init_std * np. array([
[-0.13469725, 0.1634472 ],
[ 0.13778756, -0.06120645],
[ 0.03805643, 0.24871219]])
b1 = np.zeros(3)
b2 = np.zeros(2)def predict(x):
A1 = np.dot(x,W1) + b1
Z1 = sigmoid(A1)
A2 = np.dot(Z1,W2) + b2
y = softmax(A2)
return y
def loss(x, t):
y = predict(x)
return cross_entropy_error(y, t)
def acc(x, t):
y = predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
import matplotlib.pyplot as plt
loss_W = lambda W: loss(x_e, t_e)
loss_list, acc_list = [ ], [ ]
data_list = [[[ ] for i in range(3)] for j in range(4)]
l_r , s_n = 5.0, 20
append() メソッドでグラフ要素を追加してゆく空の多次元リストを作成する方法は、次のサイトを参考にさせていただきました。ありがとうございました。
Pythonのリスト(配列)を任意の値・要素数で初期化 | note.nkmk.me
#コード4-1
for i in range(s_n):
W1 -= l_r*n_g(loss_W, W1)
b1 -= l_r * n_g(loss_W, b1)
W2 -= l_r * n_g(loss_W, W2)
b2 -= l_r * n_g(loss_W, b2)
loss_list.append(loss(x_e,t_e))
acc_list.append(acc(x_e, t_e))
for k in range(3):
data_list[0][k].append(W1[0,k])
data_list[1][k].append(b1[k])
data_list[2][k].append(W2[k,0])
for k in range(2):
data_list[3][k].append(b2[k])
Anacondaプロンプト対話モードで上掲「#コード4-0」と「#コード4-1」に続けて次の「#コード4-2」を貼り付ければ正解率と損失関数の値のグラフが…
#コード4-2
x = np.arange(len(loss_list))
plt.plot(x, loss_list, label='loss')
plt.plot(x, acc_list, label='acc', linestyle='--')
plt.xlabel("iteration") #x軸ラベル
plt.legend() #凡例
plt.show()
「#コード4-3」を貼り付ければ重みW1の1行目3要素の3D折れ線グラフが…
#コード4-3
from mpl_toolkits.mplot3d import Axes3D #3Dでプロットfig = plt.figure()
ax = Axes3D(fig)
ax.plot(data_list[0][0], data_list[0][1], data_list[0][2], "o-")ax.set_xlabel('W100') # 軸ラベル
ax.set_ylabel('W101')
ax.set_zlabel('W102')plt.show() #表示
「#コード4-4」を貼り付ければ重みW1の1行目3要素の3面2D展開図風グラフが…
#コード4-4
plt.subplot(2, 2, 2)
plt.plot(data_list[0][0], data_list[0][2], 'o-')
plt.xlabel("W100")
plt.ylabel("W102")plt.subplot(2, 2, 3)
plt.plot(data_list[0][1], data_list[0][2], 'o-')
plt.xlabel("W101")
plt.ylabel("W102")plt.subplot(2, 2, 4)
plt.plot(data_list[0][0], data_list[0][1], 'o-')
plt.xlabel("W100")
plt.ylabel("W101")
plt.show()
「#コード4-5」を貼り付ければバイアスb1の3D折れ線グラフが…
#コード4-5
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(data_list[1][0], data_list[1][1], data_list[1][2], "o-")
ax.set_xlabel('b10')
ax.set_ylabel('b11')
ax.set_zlabel('b12')
plt.show()
「#コード4-6」を貼り付ければバイアスb1の3面2D展開図風グラフが…
#コード4-6
plt.subplot(2, 2, 2)
plt.plot(data_list[1][0], data_list[1][2], 'o-')
plt.xlabel("b10")
plt.ylabel("b12")plt.subplot(2, 2, 3)
plt.plot(data_list[1][1], data_list[1][2], 'o-')
plt.xlabel("b11")
plt.ylabel("b12")plt.subplot(2, 2, 4)
plt.plot(data_list[1][0], data_list[1][1], 'o-')
plt.xlabel("b10")
plt.ylabel("b11")
plt.show()
「#コード4-7」を貼り付ければ重みW2の1列目3要素の3D折れ線グラフが…
#コード4-7
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(data_list[2][0], data_list[2][1], data_list[2][2], "o-")
ax.set_xlabel('W200')
ax.set_ylabel('W210')
ax.set_zlabel('W220')
plt.show()
「#コード4-8」を貼り付ければ重みW2の1列目3要素の3面2D展開図風グラフが…
#コード4-8
plt.subplot(2, 2, 2)
plt.plot(data_list[2][0], data_list[2][2], 'o-')
plt.xlabel("W210")
plt.ylabel("W220")plt.subplot(2, 2, 3)
plt.plot(data_list[2][1], data_list[2][2], 'o-')
plt.xlabel("W210")
plt.ylabel("W220")plt.subplot(2, 2, 4)
plt.plot(data_list[2][0], data_list[2][1], 'o-')
plt.xlabel("W200")
plt.ylabel("W210")
plt.show()
「#コード4-9」を貼り付ければバイアスb2の2D折れ線グラフが表示されるはずである。
#コード4-9
plt.plot(data_list[3][0], data_list[3][1], 'o-')
plt.xlabel("b20")
plt.ylabel("b21")
plt.show()
さらに「#コード4-10」を貼り付けると、W1、W2の小数点以下6桁で丸めた状態でW1、b1、W2、b2、グラフ要素を格納するリストが初期化される。
#コード4-10
W1 = weight_init_std * np. array([
[ 0.07395519, -0.13489392, -0.1178099 ],
[ 0.01890785, -0.02397794, 0.18300705]])
W2 = weight_init_std * np. array([
[-0.13469725, 0.1634472 ],
[ 0.13778756, -0.06120645],
[ 0.03805643, 0.24871219]])W1 = np.round(W1, decimals=6)
W2 = np.round(W2, decimals=6)b1 = np.zeros(3)
b2 = np.zeros(2)loss_list, acc_list = [ ], [ ]
data_list = [[[ ] for i in range(3)]\
for j in range(4)]
続けて「#コード4-0」以外の「#コード4-1」~「#コード4-9」を貼り付けると、W1とW2を6桁で丸めた初期値による各種グラフが撮れる。
「#コード4-10」中の「decimals=」に続く数字2か所を変更すると、丸めの桁数を変えることができる。
ただし毎回断っている通り、斎藤康毅『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』(O'REILLY) のサンプルスクリプトをダウンロードしたディレクトリに、事前に移動しておく必要があります。
今回は、まずはW1とW2の初期値に対する乗数 weight_init_std を50と大きくしてグラフのスクリーンショットを撮ってみた。すなわちバタフライ効果あるいはカオスらしき現象が起きない状態のグラフである。
バタフライ効果らしき現象が起きているグラフでは、いろんな特徴が観測され、まだまとめきれていない。
W1の2行目やW2の2列目はどうなるかについても、後日説明する予定。少しだけ先走って書いてしまうと、中途半端な対称性が現れるのだ。
「#コード4-2」による正解率と損失関数の値のグラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。


ご覧の通り、まったく区別つかなかった!
Windowsフォトで画像を順次表示させたところ、完璧に重なっていた!
「#コード4-3」によるW1の3D折れ線グラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。


「#コード4-4」によるW1の3面2D展開図風グラフ。
左:丸めなし、右:丸め6桁。

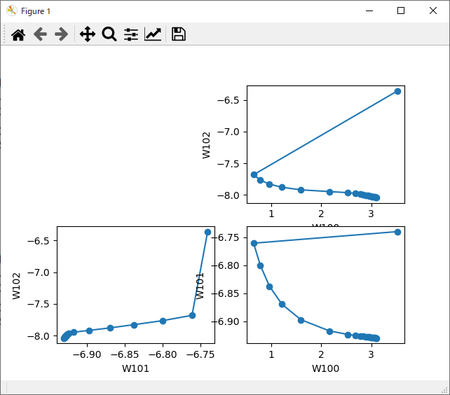
左:丸め4桁、右:丸め2桁。


「#コード4-5」によるb1の3D折れ線グラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。


「#コード4-6」によるb1の3面2D展開図風グラフ。
左:丸めなし、右:丸め6桁。
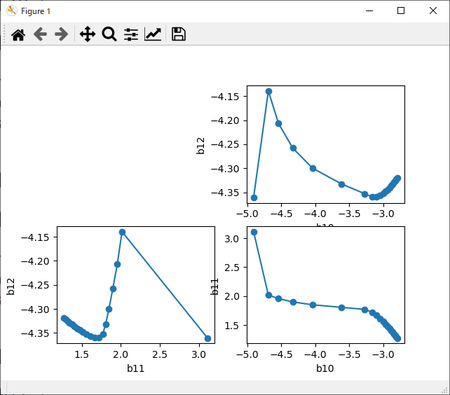

左:丸め4桁、右:丸め2桁。


「#コード4-7」によるW2の3D折れ線グラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。


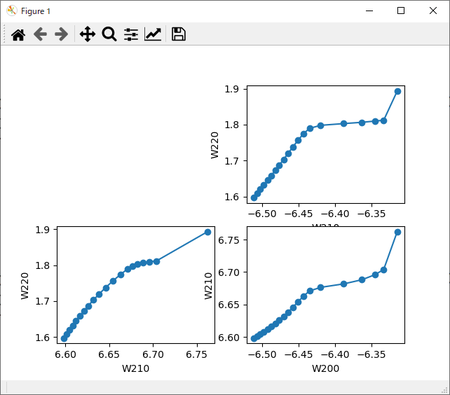
「#コード4-8」によるW2の3面2D展開図風グラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。

「#コード4-9」によるバイアスb2の2D折れ線グラフ。
左:丸めなし、右:丸め6桁。


左:丸め4桁、右:丸め2桁。


繰り返すが、寸分たがわぬグラフができたのだ!
さらにグラフを描画した後でW1、b1、W2、b2の値をダンプしたところ、私見だが驚くべき特徴が観察されたと考える!
丸めなし。
>>> W1
array([[ 3.10715279, -6.92996836, -8.0399468 ],
[-3.65469687, -2.36826359, 7.24733878]])
>>> b1
array([-2.79170761, 1.27328557, -4.31921463])
>>> W2
array([[-6.51184203, 7.94933953],
[ 6.5981932 , -2.7691377 ],
[ 1.59700312, 12.74142788]])
>>> b2
array([ 1.84055305, -1.84055305])
丸め6桁。
>>> W1
array([[ 3.10715289, -6.92996828, -8.03994567],
[-3.65469717, -2.36826367, 7.24733962]])
>>> b1
array([-2.79170755, 1.27328572, -4.3192158 ])
>>> W2
array([[-6.51184149, 7.94933949],
[ 6.59819307, -2.76913807],
[ 1.59700329, 12.74142871]])
>>> b2
array([ 1.8405531, -1.8405531])
丸め4桁。
>>> W1
array([[ 3.10710145, -6.92997272, -8.04005328],
[-3.6547279 , -2.36824909, 7.2472656 ]])
>>> b1
array([-2.79167077, 1.27327315, -4.31912361])
>>> W2
array([[-6.51186187, 7.94936187],
[ 6.59822748, -2.76912748],
[ 1.59701523, 12.74138477]])
>>> b2
array([ 1.84053306, -1.84053306])
丸め2桁。
>>> W1
array([[ 3.09749693, -6.92642448, -8.03894874],
[-3.65772763, -2.36530438, 7.2475458 ]])
>>> b1
array([-2.78123196, 1.27206239, -4.32347713])
>>> W2
array([[-6.50319204, 7.94319204],
[ 6.60072934, -2.77072934],
[ 1.59685762, 12.74314238]])
>>> b2
array([ 1.83860683, -1.83860683])
驚くべき特徴というのは、各変数で有効数字の範囲まで数字の一致が見られたことだ!
すなわち丸め2桁と4桁では小数点以下2桁まで、丸め4桁と6桁では小数点以下4桁まで、丸め6桁と丸めなしでは小数点以下6桁まで、数字が一致していた!
違いがそれだけなら、パソコンから撮ったスクショは区別つかないよね?
でも有効数字って、そういうことだったっけ?
あるいは「何を当たり前のことを」という反応が返ってくるかも知れない。
ところが weight_init_std の値を小さくしたとき、このような特徴が現れなくなるのだ。
小数点以下どころか、いちばん上の桁が一致しなくなる。甚だしい場合は、符号さえ異なることがある!
これを何かの判定基準とすることは、できないだろうか?
スポンサーリンク
