前回との違いは、重みW1とW2への乗数 weight_init_std を 0.1 とうんと小さくしたことと、繰り返し学習回数 s_n を20から100に増やしたことの2点である。繰り返し学習回数を増やしたのは、20回では正解率が100%にならなかったためだ。
その上で、np.round() メソッドの decimals オプションを 7~3 の範囲で変えてみた。すなわち小数点以下7桁から3桁までの範囲で丸めを行った。
まずは丸めをおこなわなかった場合。すなわち W1 と W2 のダンプは
>>> W1
array([[ 0.00739552, -0.01348939, -0.01178099],
[ 0.00189079, -0.00239779, 0.01830071]])
>>> W2
array([[-0.01346973, 0.01634472],
[ 0.01377876, -0.00612065],
[ 0.00380564, 0.02487122]])
である。バイアスb1とb2はゼロで初期化している。
左:前回の「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


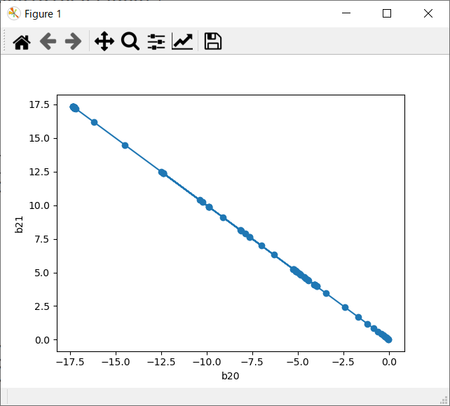
左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。

グラフ描画後の W1、b1、W2、b2 の値のダンプ。
>>> W1
array([[ 4.00632453, 0.74621904, -4.45154713],
[-4.41780543, 0.3158155 , 4.06376368]])
>>> b1
array([2.88515978, 3.49637772, 2.9176136 ])
>>> W2
array([[ 7.52188442, -7.51900942],
[ 5.85674287, -5.84908476],
[ 7.60501813, -7.57634126]])
>>> b2
array([-17.24374337, 17.24374337])
次に小数点以下7桁に丸めたケース。
>>> W1 = np.round(W1, decimals=7)
>>> W2 = np.round(W2, decimals=7)>>> W1
array([[ 0.0073955, -0.0134894, -0.011781 ],
[ 0.0018908, -0.0023978, 0.0183007]])
>>> W2
array([[-0.0134697, 0.0163447],
[ 0.0137788, -0.0061206],
[ 0.0038056, 0.0248712]])
左:「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。


グラフ描画後の W1、b1、W2、b2 のダンプ。
>>> W1
array([[ 3.44539626, 0.73045915, -4.26451676],
[-4.25213382, 0.51924299, 3.47807515]])
>>> b1
array([3.72557846, 4.69945879, 3.73723392])
>>> W2
array([[ 11.62101214, -11.61813714],
[ 11.18154668, -11.17388848],
[ 11.66302433, -11.63434753]])
>>> b2
array([-30.40488191, 30.40488191])
丸めをおこなわなかった時との違いは、有効桁数どころではない。最上位桁から違っている!
小数点以下6桁に丸めたケース。
>>> W1 = np.round(W1, decimals=6)
>>> W2 = np.round(W2, decimals=6)>>> W1
array([[ 0.007396, -0.013489, -0.011781],
[ 0.001891, -0.002398, 0.018301]])
>>> W2
array([[-0.01347 , 0.016345],
[ 0.013779, -0.006121],
[ 0.003806, 0.024871]])
左:「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。


グラフ描画後の W1、b1、W2、b2 の値のダンプ。
>>> W1
array([[-1.86501773, -4.61775425, 3.55631742],
[-1.88107736, -4.61879971, 3.55773063]])
>>> b1
array([-1.10349328, 1.53527639, -5.55997762])
>>> W2
array([[ 1.26900181, -1.26612681],
[ 4.25877394, -4.25111594],
[ 4.42342661, -4.39474961]])
>>> b2
array([-2.23040188, 2.23040188])
今回採取したデータの中では、このデータが一番奇妙に感じた。何かどう奇妙なのかは少し説明しなければならないが、後日とさせてください。
小数点以下5桁に丸めたケース。
>>> W1 = np.round(W1, decimals=5)
>>> W2 = np.round(W2, decimals=5)>>> W1
array([[ 0.0074 , -0.01349, -0.01178],
[ 0.00189, -0.0024 , 0.0183 ]])
>>> W2
array([[-0.01347, 0.01634],
[ 0.01378, -0.00612],
[ 0.00381, 0.02487]])
左:「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。


グラフ描画後の W1、b1、W2、b2 の値のダンプ。
>>> W1
array([[ 3.84608801, 0.18855283, -4.60571661],
[-4.37482109, 0.4782215 , 3.94866908]])
>>> b1
array([2.90711841, 3.87535165, 3.17658877])
>>> W2
array([[ 7.4825227 , -7.4796527 ],
[ 6.49566576, -6.48800576],
[ 7.59086115, -7.56218115]])
>>> b2
array([-17.8918042, 17.8918042])

直感 Deep Learning ―Python×Kerasでアイデアを形にするレシピ
- 作者:Antonio Gulli,Sujit Pal
- 発売日: 2018/08/17
- メディア: 単行本(ソフトカバー)
小数点以下4桁に丸めたケース。
>>> W1 = np.round(W1, decimals=4)
>>> W2 = np.round(W2, decimals=4)>>> W1
array([[ 0.0074, -0.0135, -0.0118],
[ 0.0019, -0.0024, 0.0183]])
>>> W2
array([[-0.0135, 0.0163],
[ 0.0138, -0.0061],
[ 0.0038, 0.0249]])
左:「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。


グラフ描画後の W1、b1、W2、b2 の値のダンプ。
>>> W1
array([[ 3.26082489, 0.84500467, -4.08032286],
[-4.05662297, 0.60274533, 3.3283021 ]])
>>> b1
array([3.75500344, 4.4027963 , 3.78754744])
>>> W2
array([[ 10.75561538, -10.75281538],
[ 9.77794354, -9.77024354],
[ 10.87129995, -10.84259995]])
>>> b2
array([-27.96261495, 27.96261495])
小数点以下3桁に丸めたケース。乗数を小さくとったので、有効数字は2桁程度しかない。
>>> W1 = np.round(W1, decimals=3)
>>> W2 = np.round(W2, decimals=3)>>> W1
array([[ 0.007, -0.013, -0.012],
[ 0.002, -0.002, 0.018]])
>>> W2
array([[-0.013, 0.016],
[ 0.014, -0.006],
[ 0.004, 0.025]])
左:「#コード4-3」によるW1の3D折れ線グラフ。
右:「#コード4-4」によるW1の3面2D展開図風グラフ。


左:「#コード4-5」によるb1の3D折れ線グラフ。
右:「#コード4-6」によるb1の3面2D展開図風グラフ。


左:「#コード4-7」によるW2の3D折れ線グラフ。
右:「#コード4-8」によるW2の3面2D展開図風グラフ。


左:「#コード4-9」によるバイアスb2の2D折れ線グラフ。
右:「#コード4-2」による正解率と損失関数の値のグラフ。


グラフ描画後の W1、b1、W2、b2 の値のダンプ。
>>> W1
array([[ 3.36957118, 0.62805896, -4.22677355],
[-4.21367348, 0.44197123, 3.40681463]])
>>> b1
array([3.92724771, 5.00984472, 3.93803199])
>>> W2
array([[ 13.17231312, -13.16931312],
[ 12.93812225, -12.93012225],
[ 13.20475575, -13.17575575]])
>>> b2
array([-35.21461348, 35.21461348])
生データを晒すだけでなく分析、考察を行わなくちゃいけないし、データを採っていると他にも確認したい条件が次々と出てくるのだが、とりあえずこれだけでも「ハイパーパラメータの設定が不適切だった」の一言では切り捨てられなさそうな「何かヘンなことが起きている」ことは、機械学習とカオス理論の知識のある人には伝わるんじゃないかと期待する。
先行研究も、ぼちぼち調べ始めている。
スポンサーリンク



