応用数理科学の花形である機械学習というジャンルで、しかも基本中の基本であるEOR回路を実現しようというのだから、先行研究がないわけがないとは思うのだが、自分の趣味でやっているのでいいことにする。
ジェイムズ・グリック『カオス―新しい科学をつくる』(新潮文庫)より、気象学者のエドワード・ローレンツが「バタフライ効果」あるいは「カオス」と呼ばれる現象を発見した瞬間の記述を思い出した。
一九六一年冬のある日のこと、一区切りのデータをもっと念入りに調べたいと思ったローレンツは、近道をすることにした。時間を節約するため始めの部分をはしょって、中途から処理を始めることにしたのである。まず最初の条件をコンピュータに入れておくため、前にとったプリントアウトの数字をそっくりそのままタイプしておき、コンピュータの騒音を逃れてコーヒーをのむため廊下に出た。小一時間ほどして部屋に戻った彼は、まったく思いがないもの、まさに新しい科学の種がそこに播かれているのを見たのである。
さっきローレンツが自分で数字の一宇一字をそっくりそのままコンピュータに打ちこみ、別にプログラムを変えたわけではないのだから、この結果も前のと全く同じになるはずだつた。ところが今、新しいプリントアウトを見つめるローレンツの眼前にくり拡げられていたのは、たった数カ月分の天候のパターンなのに、それが以前のものとは似ても似つかぬものになるほどの速度でずれて行くさまだった。
≪中略≫
だが次の瞬間、彼ははっと本当のことに気がついた。機械が狂ったのではなく、実は彼が打ちこんだ数字の方に問題があったのだ。コンピュータのメモリーの中には.506127という六桁の数字が記憶されていたが、紙面を倹約するためプリントアウトには.506の三桁しか印刷されない。だが千分の一ぐらいなら大した誤差ではないと思ったローレンツは、四捨五入して短くしたその三桁の数字をそのまま打ちこんだのだ。
「第1章 バタフライ効果」P33~34より。改行位置変更しています。ルビ省略しています。
バタフライ効果とは初期値のわずかな違いが結果に甚大な影響をもたらす現象、カオスとは簡明に記述できる系から予測困難な結果が出てくる現象、というふうに理解していますが、間違っていたら誰か教えてください。
ローレンツのひそみに倣って、ダンプさせたW1、W2の値を初期値としてコード中に記述し、Python のライブラリ numpy の round メソッドを使って、各桁で丸めてみた。
パラメータの数が 8+8(重みW1の形状2×4、W2の形状4×2の場合)と多く、どこから手をつけたらいいのか即座に判断付かなかったので、手軽に変更する工夫のつもりだった。
すなわち前回のエントリーに記述した「コード4」を、次のように改造して…
#コード4-1
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import *
from common.gradient import numerical_gradientx_e = np.array([[0, 0], [1, 0], [0, 1], [1, 1]]) #入力データ
t_e = np.array([[1, 0], [0, 1], [0, 1], [1, 0]]) #教師データW1 = np.array([[ 0.007111976, 0.008841753, 0.016924526, -0.022701769],
[-0.018342164, -0.000087162, 0.016726299, 0.021702541]])
W2 = np.array([[ 0.013091743, -0.003338104],
[-0.013076172, 0.00560719 ], [ 0.013749352, 0.000776133],
[ 0.000917579, 0.016105434]])
b1, b2 = np.zeros(4), np.zeros(2) #ゼロで初期化def predict(x):
A1 = np.dot(x,W1) + b1
Z1 = sigmoid(A1) #シグモイド関数P48
A2 = np.dot(Z1,W2) + b2
y = softmax(A2) #ソフトマックス関数P66
return y
W1とW2の値を、次のように丸めた。
W1 = np.round(W1, decimals=7)
W2 = np.round(W2, decimals=7)
round メソッドの decimarl オプションは、丸める小数点以下の桁数の指定である。
decimarl オプションの指定値を 2~7の範囲で変更して、続けて前回拙エントリー「#コード5」を Anaconda プロンプトに貼り付け、描かせたグラフのスクリーンショットを示す。
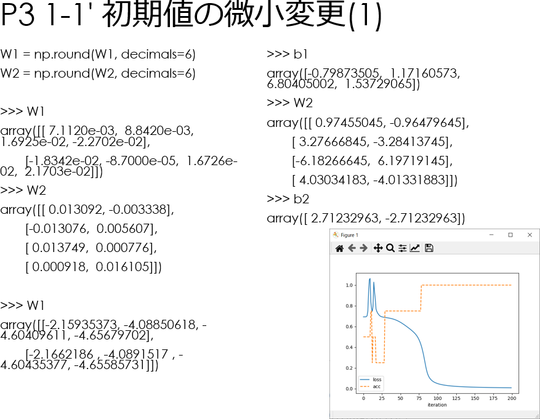
左:decimals=7、右:decimals=6。


iteration:繰り返し回数、loss:損失関数の値、acc:正解率である。以下同じ。
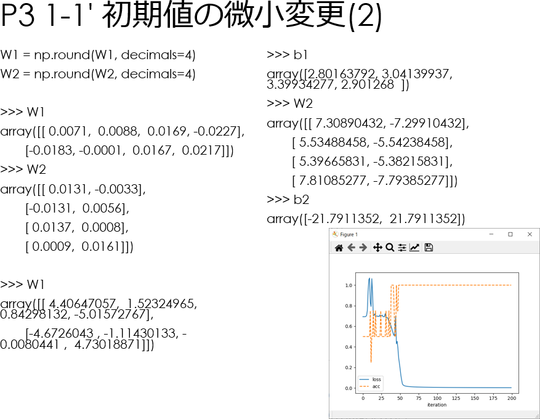
左:decimals=5、右:decimals=4。


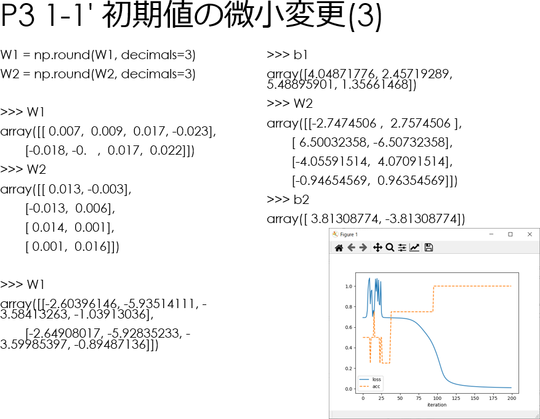
左:decimals=3、右:decimals=2


decimals=2 のグラフの形状が特異なのはなんとなく仕方ないという気がするが、decimals=3 と decimals=4 で形状が激しく変化し、decimals=5 で元に戻っているように見えるのが目を引く。
言うまでもなくdecimals=3 と decimals=4 では1/10,000以下、decimals=4 と decimals=5 では1/100,000以下の差しかないはずである。
グラフの形状が違うのみならず、収束するW1、W2、b1、b2の値も異なる。
以下に示すのは研究ノートのつもりでコード、ダンプ、スクショなど片っ端から貼り付けているpptxファイルのスクショである。
最初のW1、W2はnp.round実行後のダンプ、続くW1、b1、W2、b2はグラフ描画後のダンプである。タイトルの「P3-1-1'」というのは自分の区別用で意味はない。
上に貼ったグラフのスクショはブログを書きながら採取したものだが、pptxに貼り付けたのは5日ほど前のものだ。つまり当然ながら再現性があるということでもある。
どうも「バタフライ効果」または「カオス」と呼ばれる現象が起きていると考えてよさそうな気がする。
内部で何が起きているか、もうちょっと掘れそうなので、引き続き掘ってみる。
追記:
実務として機械学習をやってる人だったら、バタフライ効果やカオス現象には関心を向けず「ハイパーパラメータが不適切だった(この場合W1、W2の初期値が小さすぎた)」と、さっさと修正をかけるところかも知れない。
実際…
weight_init_std=1.
W1 = weight_init_std * np.array([
[ 0.07111976, 0.08841753, 0.16924526, -0.22701769],
[-0.18342164, -0.00087162, 0.16726299, 0.21702541]])
W2 = weight_init_std * np.array([[ 0.13091743, -0.03338104],
[-0.13076172, 0.0560719 ],
[ 0.13749352, 0.00776133],
[ 0.00917579, 0.16105434]])
b1 = np.zeros(4)
b2 = np.zeros(2)
loss_list = [ ]
acc_list = [ ]
learning_rate , step_num = 5.0, 50
として、
左:weight_init_std=10.、右:weight_init_std=20.のグラフ。

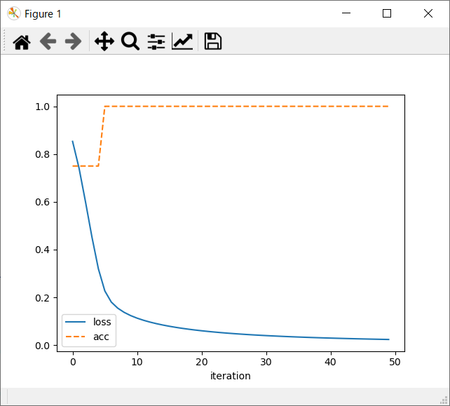
左:weight_init_std=50.、右:weight_init_std=100.のグラフ。


スポンサーリンク
