排他的論理和EORを機械学習で実現しようとしたらバタフライ効果が発生した？（その１）

すみません、対象は斎藤康毅『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』(O'REILLY) 読者限定の記事につき、新着お目汚しを避けるため日付をさかのぼって公開します。弊ブログでは、ときどきそういうことをやります。

2年半、放置しているシリーズがある。

www.watto.nagoya

方針は、排他的論理和EORを実現する重み行列 W0 、定数ベクトル b0、重みベクトル W1、定数 b1 を、機械学習によって求めることだった。

今気づいたけど、中断しているエントリーでは排他的論理和をEORではなくXORと書いてしまっているな。不統一すみません。

念のため真理値表を示す。入力データ0と入力データ1に対する教師データ0が排他的論理和、教師データ1は排他的論理和の否定である。

入力0	入力1	教師0	教師1
0	0	0	1
1	0	1	0
0	1	1	0
1	1	0	1

ところがこれが、なかなか思った通りにいかなかった。各係数がいつまでたっても収束しなかったのだ。

そこへ実生活でやっかいなトラブルに見舞われ、中途半端に放置せざるを得なかった。

トラブルはなんとか片付けるのに約2年かかった。経緯はブログに書こうかどうしようか迷っている。

半年ほど前から、機械学習の勉強をぼつぼつと再開した。2年も間が開くと、細かいところを忘れてしまっていた。ようやく中断したところまで追いついたのが、今年の年明けくらいだった。 

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

Excel への移植はしばらく諦め、Python で記述することにする。

次に示す Python スクリプトは、排他的論理和EORを実現する一例である。上掲書『ゼロから作るDeep Learning』の対応ページをコメントに示した。

以下、便宜的に「コード1」「コード2」…などと名称をつける。

#コード1
import sys, os
import numpy as np
sys.path.append(os.pardir) #P73 上位フォルダをパス指定
from common.functions import *

x = np.array([[0, 0], [1, 0], [0, 1], [1, 1]]) # 入力

W1 = np.array([[-0.5, 0.5], [-0.5, 0.5]]) #第1層 P61改変
b1 = np.array([0.7, -0.3]) #係数はP26をそのまま使用

A1 = np.dot(x,W1) + b1
Z1 = step_function(A1) #ステップ関数 P47

W2 = np.array([[0.5, -0.5], [0.5, -0.5]]) #第2層 P61改変
b2 = np.array([-0.7, 0.7]) #係数はP27をそのまま使用

A2 = np.dot(Z1,W2) + b2
y = step_function(A2) #ステップ関数 P47

print(y)

『ゼロから作るDeep Learning』まえがきvii、xiにあるサンプルスクリプトをダウンロードしたディレクトリに移動して Anagonda プロンプトの対話モード画面に上掲コードを貼り付けると、実行結果が

[[0 1]
[1 0]
[1 0]
[0 1]] 

のように表示されるはずである（Windows 10 Home、python version3.8.3にて確認）。

なお対話型モードのいいところは、プロンプトに変数を入力するだけで計算過程が表示・確認できることである。

>>> A1
array([[ 0.7, -0.3],
[ 0.2, 0.2],
[ 0.2, 0.2],
[-0.3, 0.7]])
>>> Z1
array([[1, 0],
[1, 1],
[1, 1],
[0, 1]])
>>> A2
array([[-0.2, 0.2],
[ 0.3, -0.3],
[ 0.3, -0.3],
[-0.2, 0.2]])

「A1 = np.dot(x,W1) + b1」「A2 = np.dot(Z1,W2) + b2」の "np.dot" は内積 P55、"+" はブロードキャスト演算 P14 である。

つまり第1層ではORとNANDを作り、第2層では両者のANDをとっているのである。

この係数W1、W2、b1、b2を、人間が与えるのではなく機械学習で求めたい。

試行錯誤の過程は省略し結論を急ぐ。 続いて『ゼロから作るDeep Learning』P114の2層ニューラルネットワークを改造して、次のようなコードを作成した。

#コード2
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import *
from common.gradient import numerical_gradient

x_e = np.array([[0, 0], [1, 0], [0, 1], [1, 1]]) #入力データ
t_e = np.array([[1, 0], [0, 1], [0, 1], [1, 0]]) #教師データ

weight_init_std=0.1
W1 = weight_init_std * np.random.randn(2, 2) #ガウス分布
W2 = weight_init_std * np.random.randn(2, 2) #乱数で初期化
b1, b2 = np.zeros(2), np.zeros(2) #ゼロで初期化

def predict(x):
    A1 = np.dot(x,W1) + b1
    Z1 = sigmoid(A1) #シグモイド関数P48
    A2 = np.dot(Z1,W2) + b2
    y = softmax(A2) #ソフトマックス関数P66
    return y

太字、フォント色変更をしているが Anaconda プロンプトには貼りつくはずである。

重みW1、W2の形状は2×2、バイアスb1、b2の要素数は2である。

W1、W2をガウス分布により生成された乱数で、b1、b2をゼロで初期化していること、シグモイド関数とソフトマックス関数を導入していることなど、少し説明したい箇所があるが、ざっくり省略する。

だがこれでは、思ったように動作してくれなかった。W1、W2、b1、b2を求めることができなかった。

追記：

weight_init_std の値を変更すると解が得られることがあった。だが安定的に得られるわけではない。なんでだろう？

追記おわり

追記の追記：

「#コード2」の中の教師データ t_e を真理値にすると

入力0	入力1	教師0	教師1
0	0	1	0
1	0	0	1
0	1	0	1
1	1	1	0

と1列目「教師0」がEORの否定、2列目がEORとなる。これはタネ本『ゼロから作るDeep Learning』で、出力結果にもう一段 numpy の argmax() メソッド（最大値を持つ列を取り出す関数。P80参照）を噛ませているのを、そのまま踏襲したため。

追記の追記おわり

そこで、W1の形状を2×3、W2の形状を3×2、バイアスb1の要素数を3、b2の要素数を2に変更するか…

#コード3
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import *
from common.gradient import numerical_gradient

x_e = np.array([[0, 0], [1, 0], [0, 1], [1, 1]]) #入力データ
t_e = np.array([[1, 0], [0, 1], [0, 1], [1, 0]]) #教師データ

weight_init_std=0.1
W1 = weight_init_std * np.random.randn(2, 3) #ガウス分布
W2 = weight_init_std * np.random.randn(3, 2) #乱数で初期化
b1, b2 = np.zeros(3), np.zeros(2) #ゼロで初期化

def predict(x):
    A1 = np.dot(x,W1) + b1
    Z1 = sigmoid(A1) #シグモイド関数P48
    A2 = np.dot(Z1,W2) + b2
    y = softmax(A2) #ソフトマックス関数P66
    return y

またはW1の形状を2×4、W2の形状を4×2、バイアスb1の要素数を4、b2の要素数を2に変更にしたところ…

#コード4
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import *
from common.gradient import numerical_gradient

x_e = np.array([[0, 0], [1, 0], [0, 1], [1, 1]]) #入力データ
t_e = np.array([[1, 0], [0, 1], [0, 1], [1, 0]]) #教師データ

weight_init_std=0.1
W1 = weight_init_std * np.random.randn(2, 4) #ガウス分布
W2 = weight_init_std * np.random.randn(4, 2) #乱数で初期化
b1, b2 = np.zeros(4), np.zeros(2) #ゼロで初期化

def predict(x):
    A1 = np.dot(x,W1) + b1
    Z1 = sigmoid(A1) #シグモイド関数P48
    A2 = np.dot(Z1,W2) + b2
    y = softmax(A2) #ソフトマックス関数P66
    return y

機械学習によりW1、W2、b1、b2を求めることができた！ なんでだ？？

すなわち上掲「コード3」または「コード4」と、次に示す「コード5」をAnacondaプロンプトに貼り付けて、正解率accと損失関数の値lossのグラフを表示させたのである。

損失関数のグラフは『ゼロから作るDeep Learning』P119図4-11、正解率のグラフはP121図4-12を

#コード5 ch04\two_layer_net 改造
def loss(x, t): #損失関数
    y = predict(x)
    return cross_entropy_error(y, t)

def accuracy(x, t): #正答率
    y = predict(x)
    y = np.argmax(y, axis=1)
    t = np.argmax(t, axis=1)
    accuracy = np.sum(y == t) / float(x.shape[0])
    return accuracy

import matplotlib.pyplot as plt #グラフ描画準備
loss_W = lambda W: loss(x_e, t_e)
loss_list = [ ]
acc_list = [ ]
learning_rate = 5.0 #学習率
step_num = 200 #繰り返し回数

for i in range(step_num): #繰り返し学習
    W1 -= learning_rate*numerical_gradient(loss_W, W1)
    b1 -= learning_rate*numerical_gradient(loss_W, b1)
    W2 -= learning_rate*numerical_gradient(loss_W, W2)
    b2 -= learning_rate*numerical_gradient(loss_W, b2)
    loss_list.append(loss(x_e,t_e))
    acc_list.append(accuracy(x_e, t_e))

x = np.arange(len(loss_list))
plt.plot(x, loss_list, label='loss')
plt.plot(x, acc_list, label='acc', linestyle='--')
plt.xlabel("iteration") #x軸ラベル
plt.legend() #凡例
plt.show()

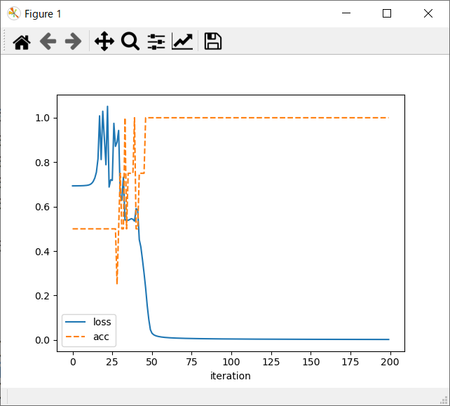
 これはたった今、コード3とコード5を貼り付けて実行した結果…

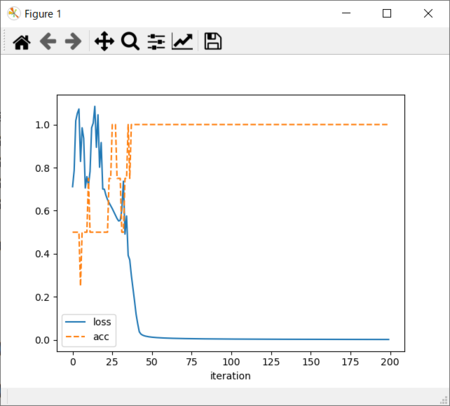
これはコード4とコード5を貼り付けて実行した結果、得られたグラフである。

iterationは繰り返し回数である。損失関数の値lossは0に近いほどよく、正解率accは1になってほしい。

今回はたまたま、コード3+コード5もコード4+コード5も期待通りの結果が得られた。

ところが、実行するたびにグラフの形状が激しく違ったのだ！

正解率が1にならない、すなわち学習結果が正しく得られないことも、少なくなかった！

いったい何が起きているのだろう？

ということで、もう少し深く掘ってみることにした。

明快な結論が出せたわけではないが、それでも少しわかったことがあるので、だらだら続けようと思う。

スポンサーリンク