このホッテントリに関連して、たまたまちょうどよいサンプルを見かけたところなので、ささっとエントリーに仕立ててしまいたい。
おっしゃることはごもっともだと思う。心情的には同意したい。しかし、数式には、結城先生が連ツイ中で例として引いている漢字や英語にはない怖さがあると思う。その怖さは、むしろ「文系」の人より「理系」の人のほうが、わかってもらえるんじゃないだろうか? つまり「数式アレルギーの理系」の人がいたっておかしくないんじゃなかろうか? どころかアレルギーの度合いは、ひょっとしたらそういう人の激しいんじゃなかろうかとすら想像する。
怖さというのは、数式の難易度が、見た目からは即座に判断できないということが、ままあるということだ。
スポンサーリンク
こんな数式がある。
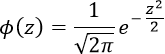
標準正規分布の確率密度を与える関数である。「理系」の人間だったら、知らないと恥ずかしいというレベルの数式であろう。この関数にはどんな特徴があるか(例えばマイナス無限大からプラス無限大の範囲で積分すると1になるとか)、係数の1/√2πにはどんな意味があるのかなどは、大学1年を終えた段階で理解していなかったら、容赦なく再履修を食らうであろう。
一方、こんな数式もある。
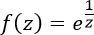
先の数式に比べて、見かけはむしろ簡単だ。慣習として変数に “z” を用いるところまで似ている。だが変数の定義域を複素数とすると、事情は大違いだ。これは関数論(複素関数論)で「真性特異点」を持つ最も簡単な関数の一つである。関数論で真性特異点に関しては「ピカールの定理」という重要な性質が知られている。真性特異点の近傍では、高々二つの値を除いたマイナス無限大からプラス無限大までのすべての値(どころか複素平面上のすべての値)を無限回とるという、ちょっと聞いただけでは理解できないような定理だ。
「ピカールの定理」の証明が日本語で読めるのは、他にないことはないと思うが私が知っている範囲では吉田洋一『函数論 (岩波全書 141)』くらいである。同書全14章中の第9章(「IX章 Picardの定理」と表記)丸々一章を証明に充てている。私は工学部出身だが、大学院修士課程時代にチャレンジして早々に挫折した。当時の観測範囲では、周りに「ピカールの定理」の名前だけなら知っている学生は何人もいただろうが、工学部だと証明まで理解している人間は、いたとしてもほんの一握りだったんじゃないだろうか?
数学専攻の人からはひょっとしたら「こんなものを難解扱いするなんて」と馬鹿にされるかも知れない。しかし、もしそんなことがあれば、工学部の側でも数学の人にはなじみがないであろう難解な(だが工学では有用な)数式を、いくらでも持ち出して相手を煙に巻くことは可能なのだ。
そうそう、数式にはそういう厄介な点もあるんだった。数式と一口に言っても、工学で、数学で、あるいは物理で、よく用いられるものは全然違うということもありうるのだ。例にはならないかも知れないが、虚数単位は数学ほか一般的には “i” で表すが、電気工学に限っては “j” を使うんですよ。 “i” は電気工学の最重要概念である「電流」に使いたいからだ。
漢字や英単語で見たことのないものはいくらでもあるが、意味を理解するのに、数式と同じくらい手間がかかるものは、たくさんあるものだろうか? ないことはないかも知れないけど、多くはないんじゃないかな? 専門用語などに、専門書を半分くらい読まなきゃ理解できない言葉は、ないことはないのか。今ぱっと思いついたのはカント哲学の「物自体」とか。でもそれを文中に出すなら、意味を説明するのは著者の側の義務じゃないかな?(私自身が義務を果たしてないな。「物自体」というのは、えーっと、えーっと、難しい言葉です)
数式も漢字や英単語と同じくコミュニケーションの手段であるという点においては、結城先生の論旨に同意である。しかし上に述べた意味で、配慮を求められるのは、圧倒的に発信側じゃないだろうか? 文章中に数式を使用した場合、もしその文章が一般の読者に向けたものであるならば、その数式はどんな意味を持ち、主にどんなジャンルで用いられるもので、難易度はどのくらいか(高校数学? 大学共通科目? 大学専門科目? 大学院? 研究者レベル?)くらいは、普通の言葉で説明を加えるくらいの配慮はあってしかるべきなんじゃないかとも思うのだが、いかがでしょうか。
自慢じゃないが私は「ピカールの定理」はじめウィキペの数学関連項目に書いてある数式を、満足に理解できたためしは滅多にないぞ( ̄^ ̄)
追記:
「物自体」に関しては、以前に怪しげなエントリーを仕立てたことがあるのでリンク貼らせてもらいます。
追記の追記:
すごいの来た。そうだよな、こういうのが来るだろうなと、うすうす予感はしていたのだ。悔しいのでぶくまするだけでなくリンクも貼ってしまう。
スポンサーリンク
