Microsoft Mathematics が標準正規分布関数を計算してくれないのは、わかった。ではどこまでなら計算してくれるのかを、やってみた。
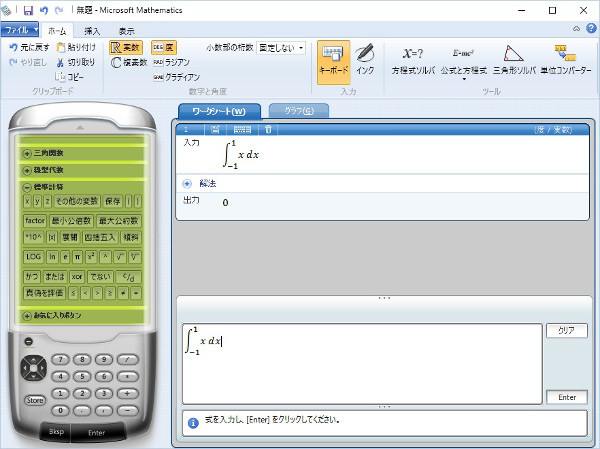
まずはf(x)=xの、区間 [-1,1] での定積分。いくらなんでもこれはやってくれなきゃ。
スポンサーリンク
「⊕ 解法」というのまで出してくれた。「⊕」をクリックすると、次のように説明してくれた。

次に、f(x)=exp(x)の、やはり区間 [-1,1] での定積分を求めてみた。
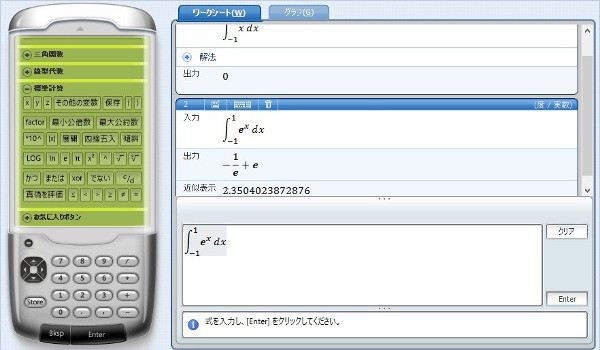
計算はしてくれた。ただし解法までは表示してくれなかった。
次は、f(x)=exp(-x)をやってみた。
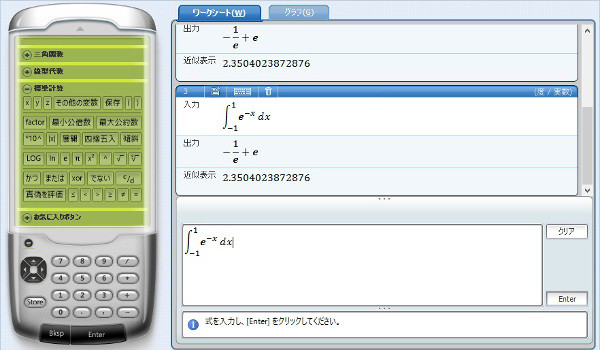
これも、できた。
いよいよf(x)=exp(-x^2)。
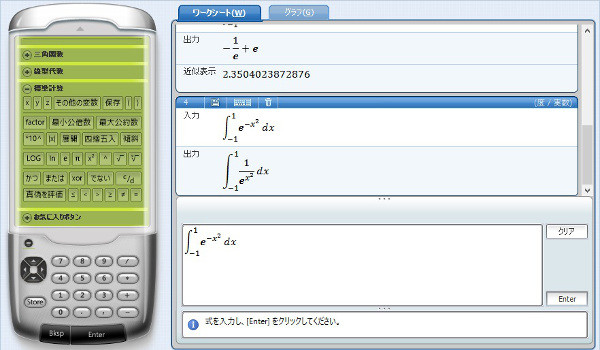
ここで力尽きたか!
ちなみにこの積分には「ガウス積分」という名前がついていて、Wordの数式のメニューの「Office.com のその他の数式(M)」からワンクリックで挿入できてしまう!
Wordドキュメントに挿入したところ。
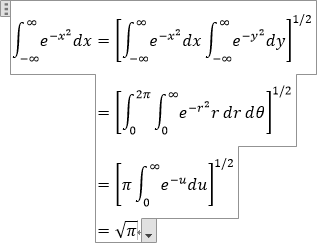

くらいの悪態はつきたいものである。
ちょっとフォローすると、Wordで作った数式をMathematicsにコピーしても計算してくれるなど、便利なことは他にもあるんですよ。
それはともかく、実は標準正規分布や正規分布を与える関数は、Excelのほうに完備されているから、そっちを使えばいいという話はある。
いつもの教科書『新確率統計』のP71に、こんな例題がある。
[例題6] Z が標準正規分布に従うとき,次の確率の値を求めよ.
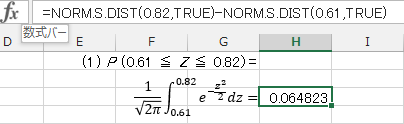
(1) P (0.61 ≦ Z ≦ 0.82)
(2) P (Z ≧ 1.57)
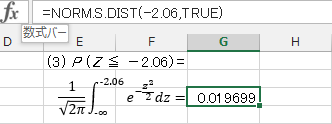
(3) P (Z ≦ -2.06)
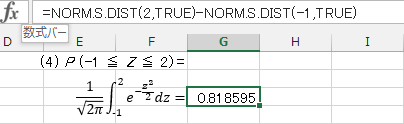
(4) P (-1 ≦ Z ≦ 2)
外見は数学の数式と似ても似つかないが、これらはExcel関数 “NORM.S.DIST”(Excel2007以前では “NORMSDIST”)を使って解くことができる。標準正規関数の、負の無限大からの累積値を与える関数だ。
まずは(1)。参考までに数式を挿入している。ExcelでもWordと同様に数式を挿入することができるが、ただのコメントにすぎず関数の値を求めるのに何の役割も果たしていない。関数の使い方は「数式バー」を参照ください。
(2)。正の無限大からの累積値を求めるためには、標準正規分布が偶関数であることを利用し、積分区間を [1.57,∞] から [-∞,-1.57] に変換していることに注意。

(3)。
(4)。
思うに、Excelの弱点の一つは、分数を分数形式のまま扱うことができないことじゃないだろうか。だからExcelでは、組合せや二項分布を扱うことはできない。できるかも知れないけど私は知らない(追記:すみません、できます。組み合わせはCOMBIN関数、二項分布はBINOM.DIST関数というのが用意されています。お詫びして訂正します)。『新確率統計』とともによくタネ本に使わせてもらっているインプレス「できるシリーズ」の『やさしく学ぶExcel統計入門』は、とてもよくできた本だと思うが、順列、組合せ、二項分布をガン無視している点が玉に瑕だと思う。二項分布は正規分布やポアソン分布と密接な関係があり、タイトルで統計を名乗る本が扱っていないのは、ちょっと物足りない。
(追記:すみません、こちらもP74に「試行回数を増やすと正規分布に近づく」と紹介されていました。「用語集」と「関数INDEX」にも載っていました。「ガン無視」ってことはなかったです。失礼しました)
想像なんだけど、combination関数のようなMicrosoft Mathematicsのいくつかの機能は、Excelの将来のバージョンでの採用を検討するため開発されたものじゃないだろうか?
ただし最新バージョンであるExcel2016には未搭載のようだ。「Excelで分数をどう扱うか」という宿題が解決されていないからであろう。
なんでそう考えるかというと、Microsoft Mathematics には「インク」という機能がある。数式をドラッグで入力する機能だ。
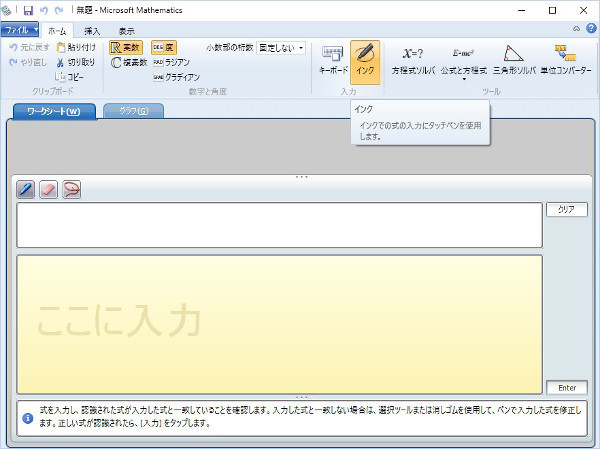
まあアホなんですけどね。

この「インク」という機能は、WordほかOffice2016に新機能として鳴り物入りで追加された。私のパソコンは2013しかインストールしてないので、他人のパソコンを使わせてもらいスクリーンショットを撮った。

やっぱり使えなかった。

追記:
すみません、Excel2013には組合せを計算する関数 “COMBIN” が実装されています。「組合せ」で検索すると出て来ませんが「組み合わせ」で検索したら見つかりました。お詫びしつつ訂正します。
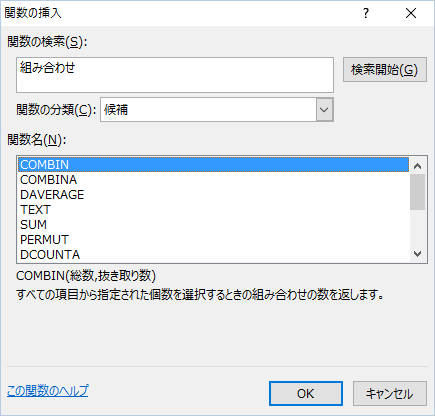
二項分布関連でも、“BINOM.DIST” 関数他いくつかのバリエーションが用意されていました。こちらもお詫びしつつ訂正します。

スポンサーリンク
※ リンク集(随時追加)
Microsoft Mathematics 私家版順不同リファレンス
