このエントリーは自分用メモが主目的なので、日付をさかのぼって公開しています。こうすると、読者登録していただいている方の新着情報に出にくくなるので、目立たなくするための工夫のつもりです。
ここのところ「あれっ?」と思うほど新規に読者登録していただいた方の数が増えています。ありがたいことではあるのですが、率直に言って「ブログバブル」の傾向があるように考えています。昨日も、月収153万円を稼いだという大学院生ブロガーさんの記事が、ホッテントリになりました。それはそれで結構なことだと思います。しかし、当方は足掛け13年ブログをやっていますが、ブログ稼業がこれほど話題にされるようになったのも、また弊ブログのアクセスが急増したのも、ほんのここ2、3年のことです。「こういうことは、あまり長続きしないだろうな」という確信めいた予感があります。機会あるごとに繰り返していますが、弊ブログの主目的は自分用メモです。こういう時期こそ、あえて意識して以前と同じペースの更新を続けようと考える次第です。
スポンサーリンク
三次関数 y = x^3 + a x^2 + bx + c の、a、b、c を様々に変えた場合の極大値、極小値、そして変曲点の座標を計算する必要が生じた。なんでそんなことをしなければならなくなったかは内緒。例によって、Microsoft Mathematics を使うとべらぼうに楽なのである。しかし忘れちゃうので、スクショを撮って自分用のメモにするとともに、検索で探している人に「こんなものでもよろしければ」と提供しようと考える次第。
目次
グラフの概形を表示する
Microsoft Mathematics を起動し「グラフ(G)」タブに切り替えて、「方程式と関数」欄に数式を入力する。画面は「 y = x^3ーx^2-x + 1 」という関数のグラフを描かせようとしているところ。全部半角で、この通りに入力すればよい(ブログでは演算子が半角だと見づらいので全角にしています)。

上掲画面の真ん中下方に見えている「グラフ」というボタンをクリックすれば、グラフを描いてくれる。必要に応じて左上の「ズームイン」や「ズームアウト」を使うといい。

極大値と極小値を求める
極値を求めるには、まず関数の微分を求める。「ワークシート(W)」タブに切り替え、画面左端の「微積分」ボタングループから「d/dx」(導関数)というボタンをクリックする。すると、画面下部の入力ペインに導関数を求めるための数式が表示される。

三次関数の数式は、手入力してもいいが、一旦「グラフ(G)」タブに戻って、「方程式と関数」欄からコピー&ペーストするのが楽だろう。
右下の「Enter」ボタンをクリックすると、導関数すなわち関数を x で微分した結果が、出力ペインに表示される。

導関数がゼロになる値が極値である。極値の x 座標を求めるためには、導関数をイコール 0 と置いて、二次方程式として解けばいい。
そのためにはいくつかの方法があるが、Microsoft Mathematics には方程式を解くための “solve” という関数があるので、今回はそれを使ってみた。
入力ペインに “solve(” と手入力する。続いて出力ペインの「出力」欄の数式、すなわち元の関数の導関数をダブルクリックすると、数式が “solve(” の後ろに表示される。

数式の後ろに “=0)” と手入力して「Enter」ボタンをクリックすると、出力ペインに方程式を解いた結果が表示される。
すなわち導関数の値が 0 となるのは、x の値が -1/3 のときと 1 のときである。

y 座標の値を求めるために、Microsoft Mathematics の「リストに機能」というのを使う。リスト機能に関する説明は、下記リンクの弊記事を参照のこと。
Microsoft Mathematics 私家版順不同リファレンス|変数への値の代入、リストによる変数への値の代入 - しいたげられたしいたけ
入力ペインに “{” を入力して、出力ペインの「解1」、「解2」をダブルクリックすると、 “{” の後ろに解1、解2が表示される。ただし “x =” という余計なものも入力されるので、手作業で削除する必要がある。また値を区切る “,” も手入力する必要がある。
今回のように “x =-1/3” 、“x = 1” のような簡単な値なら、全部手入力した方が早いかもしれないが、分数や根号を含む一般的な複雑な形の解の場合は、ダブルクリックを使った方が楽である。

“}” を入力し、画面左下の「Store」(変数に値を保存する)ボタンをクリックすると、“}” の後ろに “→” が表示される。“→” の後ろに “x” を入力し、入力ペイン右下の「Enter」ボタンをクリックする。

その後、入力ペインに再び三次関数をコピペし「Enter」ボタンをクリックすると、x に-1/3 と 1 を代入した結果が表示される。これらが極値の y 座標である。
すなわちグラフの極大値の座標は (-1/3, 32/27) 、極小値の座標は (1,0) であることがわかった。

変曲点を求める
画面左側の「微積分」ボタングループより「2階導関数」ボタンをクリックする。

この状態で、出力ペインの三次関数の数式をダブルクリックすれば、数式が入力ペインのカッコの中に入るのである! コピペするより楽なのだ!

「Enter」ボタンを入力すると、三次関数の二階導関数が出力ペインに表示される。
x にリストの値を代入した結果も表示されるが、無視する。

変曲点すなわち二階導関数の値が 0 になる x の値は 1/3 である。
これをリストに代入する。
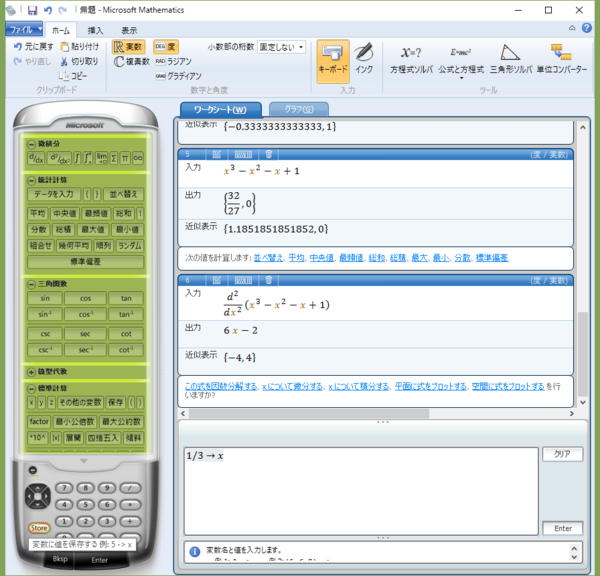
念のために出力ペインの “6x-2” をダブルクリックして計算させたところ。当然 0 になっている。このくらいは暗算できるが、あくまで念のため。

出力ペインを少し上方にスクロールすると元の三次関数の数式があるので、それをダブルクリックして「Enter」ボタンをクリックすると、数式に “x=1/3” を代入した値が得られる。16/27 というのが変曲点の y 座標である。
すなわち変曲点の座標は (1/3,16/27) である。
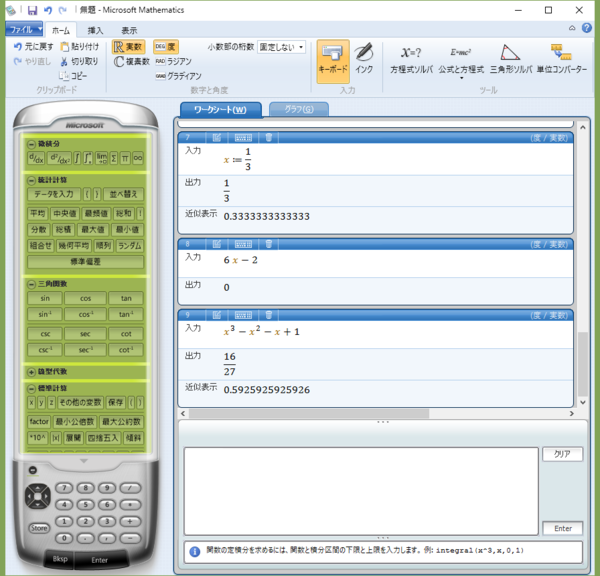
区間[-1,1]における定積分
ついでと言っては何だが、この三次関数の、区間[-1,1]における定積分も求めてみよう。簡単なので。
「微積分」ボタングループの「関数の定積分」ボタンをクリックすると、入力ペインに定積分のための積分記号が表示される。

三次関数は、出力ペインからダブルクリックすれば被積分関数に表示される。積分区間 “-1” 、“1” は手入力する。
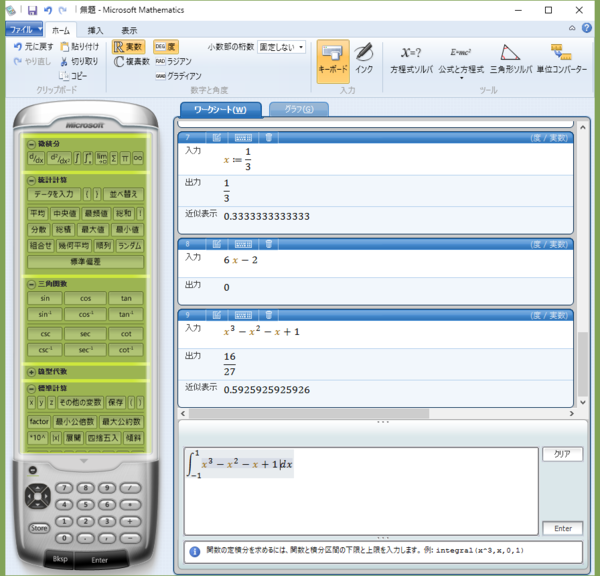
「Enter」キーをクリックすれば、4/3 という積分値が得られる。
リンク(随時追加)
Microsoft Mathematics 私家版順不同リファレンス
Microsoft Mathematicsを使ってみたら賢いのかアホの子なのかよくわからないが多分WordやExcelの補完ツールとして使うのが適切なのかなと思った
