「0.999999... = 1」にまつわる未整理材料いろいろ(その1) の続き(すなわち「その2」)を書こうとして、1ヶ月以上書きあぐねている。結論はすでに頭の中にあるのだが、未整理材料というのを取り出すのに手こずっているのだ。
実数の公理を論じる上での実例として √2 (ルート2)が扱いやすいかな思ったので、ちょっといじってみた。そうしたら、行列を使うと便利かなと思われる場面が出てきた。これのどこが珍しいかというと、大学初年度の数学の定番である「初等解析」と「線形代数」のコラボとなるのだ。なので、独立した話題として書いてみる。
√2 が無理数である証明は、中学数学で出てくる。また、√2 の近似値は、次の連分数より求めることができる。

「ナニコレ?」と思われるかも知れませんが、説明は「google:ルート2 連分数」で検索すれば出てきます。書籍だと、手元にあるのは『連分数のふしぎ (ブルーバックス)』のP83~84。
これを、次のような数列 an(n=1、2、3・・・)と見て値を計算してみる。
a0 = 1/1 = 1
an = 1/(1+1/an-1) (n=1、2、3・・・)
電卓でも計算できるが、Excelで計算するとメチャ楽なのでやってみた。
セルE1のみ数値「1」を入力し、数式バーに表示されているセルE2の数式を、セルE3以降にドラッグでコピーした。G列はE列の2乗を計算している。

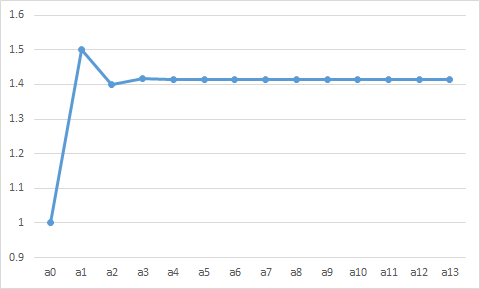
折れ線グラフも描いてみた。数字を見ると小刻みに増減を繰り返しているが、グラフは急速に一定の値に収束していることがわかる。
スポンサーリンク
なんでこんなことをやろうと思ったかというと、初等解析で出てくるコーシー数列の、わかりやすい実例にならないかなと思ったからである。
一見して特定の値に収束しているのは明らかなように見えるが、本当に収束しているだろうか。ひょっとしたら小数点以下はるか下の方で、ずっと周期変動とかはしていないだろうか。それを数学的に確認してみたい。
いつものタネ本である『無限級数 (数学ワンポイント双書 (17))』P28より引用する。
{xn}を1つの数列とし,ε >0を任意に与えられた数とする.このとき,これに応じて1つの数 N を定めることができて,p および q が N よりも大きい限り,どんな数であっても
| xp - xq | < ε
とすることができるとき,数列{xn}をコーシー数列という.
これはもちろん.数列{xn}が収束する数列であることとは意味が違う.しかし,次の定理が証明される:
[定理]「数列が収束するために必要で十分な条件は,それがコーシー数列であることである.」
(上掲書P29)
これに続いて定理の証明があるが省略。多くの大学の初等解析(微積分)の教科書に載っているはずだ。
この定理を使って、上記数列 an の収束を確認することはできないかと考えた。結論を先に書いてしまうと、数列 an は n の関数として書きなおすことができ、コーシー数列の収束の定理を使わなくても収束することがわかったのであるが。
先走っても仕方がない。まずは a0 ~ a5 の式を、漸化式として書き出してみる。いつもの通りWordの数式で作成して画像データで貼っています(コピペで Microsoft Mathematics に貼りつけ計算させられるので、重宝しています)。
右側には、それぞれの2乗値と、2との誤差も計算してみた。

これではどうも、何かわかったような気がしない。そこで ak を基準とした ak+1 ~ ak+5 の漸化式を書いてみた。

k = 0、a0 =1 と置いたとき、a1 = 3/2 = 1.5 *1、a2 = 7/5 = 1.4、a3 = 17/12 = 1.416666…、a4 = 41/29 = 1.413793…、 a5 = 99/70 = 1.4142857…ということで、ひとつ前に掲げた式と一致する。
これでも何かがわかったような気はしない。だがよく注意をすると、分子の ak の係数と、分母の定数項が常に一致しているようだ。さらによく見ると、分子の定数項は分母の ak の係数の2倍になっているようだ*2。
つまり

において、 xl = 2wl 、yl = zl となりそうだ。
これらは、 ak を次のように置いて、 ak+1 を書いてみると、常に成り立つことが確認できる。
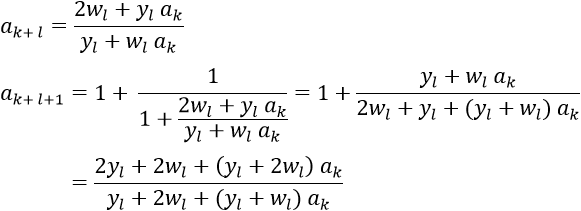
それではこの yl = 1, 3, 7, 17, 41, 99…、 zl = 1, 2, 5, 12, 29, 70… (l = 0, 1, 2, 3, 4, 5…)という整数列の正体は、何だろうか?
等差数列だと仮定しても等比数列だと仮定しても、うまくいかなかった。結局その正体を突き止めるためには、行列の知識が必要になった。
結論を記すと、こういうことだ。次のような行列表記は、汎分数を解消する計算手順を検討すれば、すぐに出てくる。

y0 = 1、 z0 = 1 だから、l = 1, 2, 3, 4 ,5 を計算してみると
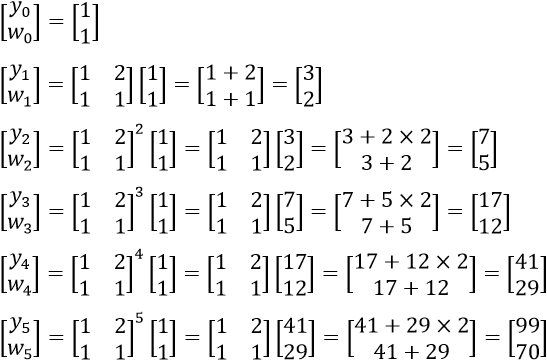
繰り返しになるが、これのどこが嬉しかったかというと、大学初年度の数学の定番でありながら、あんまり重なるところがあるようには見えない初等解析(微積分の基礎づけの部分)と線形代数が、珍しく(?)共演しているように見えたからだ。
そこで、曲がりなりにもなんらかの結論がだせないだろうかと、もうちょっといじってみる気になった。
以下、「後編」に続きます。だいたい準備はできているので、「0.999999... = 1」にまつわる未整理材料いろいろ(その1) のときのように、1ヶ月以上経っても「その2」が書けない、なんてことにはならないと思います。すいません。
つかこの記事自体が「その2」なのだと主張することはできるのか。
あと『連分数のふしぎ』は好著です。とりわけ、自然が数学を使って描き出した鮮やかな造形を論じた「CHAPTER7 連分数と黄金比と松ぼっくり」(P214~)は、数学好きにとっては書店店頭の立ち読みでもいいから一見の価値ありです。
追記:
2回で完結されられず前編・中編・後編の3回になりました。
続きです。
スポンサーリンク
*1:誤記訂正しました。 b:id:t_massann さんご指摘ありがとうございました
*2:分母と分子が逆だったので訂正しました。 b:id:t_massann さんご指摘ありがとうございました
