ピーター・ペジック、山下純一(訳)『アーベルの証明―「解けない方程式」を解く』（日本評論社）

アーベルの証明―「解けない方程式」を解く

数式のない数学の本は隔靴掻痒で物足りない、さりとて数式だらけの専門書は歯が立たない、というわけで、私にはこのくらいのレベルの本がちょうどいいです。ぶっちゃけ高校数学の、微積が出てくる直前あたりですな（実際には全１０章中第８章以降は「置換」「対称」の話を経て群論に移行するが。すなわち大学数学）。ま、例えばこんな具合です…

３次方程式の解の公式
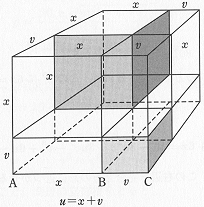
「立方と辺の6倍の和が20になる」というカルダーノの例，つまり３次方程式x³+6x=20を考えよう．この方程式を完全立方の形にしたい．まず，x=u-vと置くというトリックが必要だ．上の図で，x³は大きい方の影を付けた立方体の体積で，１辺がAC=uのさらに大きな立方体に埋め込まれている．１辺がBC=vの小さい方の影を付けた立方体もある．１辺がuの立方体から１辺がxの立方体を切り出すには，３回の切断が必要だ．1回の切断によって，体積がu²vの直方体が切り取られるが，こうしてえられる３個の直方体は重なっている．２個の直方体の重なった部分の直方体の体積はuv²となる．ただし，３個の重なった部分がまた重なっており(つまり，３重に重なった部分があり)，それは立方体で体積はv³である．したがって，象徴的に書けば，
　　x³=u³-((切り取られる直方体３個の体積)
　　　　　　-((重なり全体の体積)
　　　　　　-(重なりの重なりの体積)))
つまり，
　　x³=u³-3u²v+3uv²-v³
となる．最初の方程式にするには，この x³に6x=6u-6vを加えればよい．
こうして，
　　x³+6x=u³-3u²v+3uv²-v³+6u-6v
がえられる．この右辺を完全立方の形に近づかせるために，とりあえず

　　-3u²v+3uv²-v³+6u-6v=-3(uv)u+6u+3(uv)v-6v
　　　　　　　　　　　　　　　　　　　=-3u(uv-2)+3v(uv-2)
　　　　　　　　　　　　　　　　　　　=-3(uv-2)(u-v)
が消えてくれるとうれしい．そのために強引にuv=2と考える．こうすれば，明らかに
　　-3u²v+3uv²-v³+6u-6v=0
となる．立方完成をめざして，uとvが関係式uv=2を満たすものと考えるわけだ．
あとはやさしい．

（p35〜36 図も）
３次方程式の解の公式導出目前まで。残念ながら私には数学センスはないが、このような数式を「美しい」と感じる能力は、かろうじて備わっているようである（リーマンのゼータ関数の「美しさ」はわからないが、オイラーの公式の「美しさ」なら理解できるレベル）。
とは言うものの、本書巻末の付録に収められているアーベルの原論文そのものを理解するのには、相当に骨が折れるのだが。
なお、（本来はこの本に限ったことではないのだが）訳書というものは原著者と翻訳者の共同作業の賜物なのだなあと、あらためて感じる。
スポンサーリンク