前回のエントリー には、予想を上回るアクセス、はてなスター、コメント、ブックマークコメントをいただいて、感謝しています。
お一人だけ取り上げるのは申し訳ないんですが、b:id:sea_side さんのブコメに乗っからせてもらいます。つかまんまです。ご指摘ありがとうございました。
意外と楽しい「平均」の世界あるいは相加、相乗、調和平均の例題として40と60という数値がピンポイントで絶妙である件 - しいたげられたしいたけ
- [!エントリー]
- [数学]
こんなところにまで現れるというのか、妖怪1足りない!つか二乗平均だとだいたい51やね。
2016/05/18 07:41
スポンサーリンク
ウィキペ「二乗平均平方根 - Wikipedia」を参考に、2項a、bの場合の式を示すと、これでいいのかな? 例によって数式はWordで作成したキャプチャです。
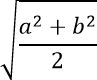
a = 40、b = 60とすると、確かに51に近い値になることが、またしても暗算レベルで確認できてしまうのだ!
ルートの中のみを示すが…

ここで、またしても「妖怪1足りない」が登場する!
あえて1を足すことによって、二乗形式にすることができるのだ!

電卓で計算すると、√1/2×(40×40+60×60) = √2400 √2600*1 = 50.990… で誤差はやはり小数点以下2桁目に出た。
なお「二乗平均平方根 ≧ 相加平均」となることも、2項の場合であれば簡単に確認できる。両者の二乗の差を取ればいいのだ。

a = b のときに等号が成立するのも明らかだ。
ちなみに「妖怪1足りない」は、数学や物理の世界では、いろんなところに出没する。
とっさに思いつくのはの、黒体輻射の温度と周波数の関係を表す「プランクの公式」で、この式の分母のマイナス1が量子力学を拓く嚆矢となったことは有名である。
統計学で、不偏分散を計算するときにnではなくn-1で割ることも、必ず議論に上る話題である。
「ラマヌジャン マイナス1」で検索して出てくる項目は、私の理解可能範囲を完全に超越している…
追記:
さらに続編を書きました。
スポンサーリンク
*1:すみません、ミスです。browncapuchin さんご指摘ありがとうございます