O'REILLY『ゼロから作るDeep Learning』5章誤差逆伝播法は見かけに反して意外な難関だった（その2）

5章では、自分自身に出題する演習問題を2問作ってみた。

1問目は、6月25日付エントリーに書いた「2章パーセプトロンによる論理ゲート」を誤差逆伝播法で機械学習させてみよう、というものだ。同日付では数値微分法で解いた。

watto.hatenablog.com

まずはパーセプトロンによる論理ゲートの損失関数を求める Python スクリプトを、「計算グラフ」で表現してみた。まずは順伝播のみ図示している。O'REILLY『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』（以下 “テキスト”）で計算グラフが登場するのは5章と付録Aのみだが、学習する側としては、もうちょっと前から使ってもよかった。

スポンサーリンク

Sigmoidレイヤの逆伝播の計算は、テキストP143～146にていねいに解説されている。ここではテキストP145図5-20の完成図を模写したものだけを示す。

テキストではさらに変形を行って、結論として y(1－y) という形の式を得ている（P146）。

これに倣って、2乗和誤差の逆伝播を求める式を計算してみた。2乗和誤差の逆伝播はテキストには載っていないが、P130～132 の z = t **2、 t = x + y という例題を改造すれば、簡単に求められる。なお 6月25日付弊エントリー では、0.5 を乗ずるのを忘れていたのに気がついた。0.5 を掛けた方が、逆伝播を与える式の形が簡単になる。

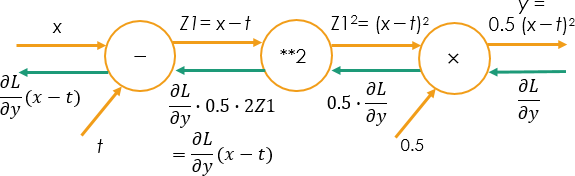
結論として式の形は x－t となる。

これらを最初の計算グラフに書き込んでみた。すなわちパーセプトロンによる論理ゲートの逆伝播は、下図のようになるはずだ。

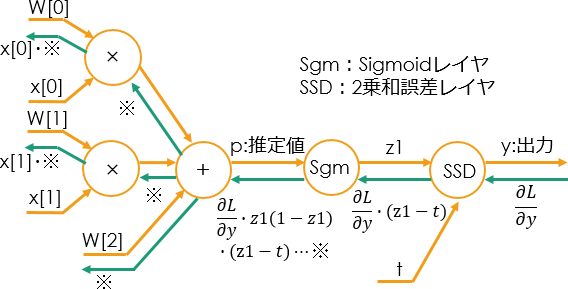
この図を基に、6月25日付弊エントリー に示したクラス “Perceptrn” を書き直してみた。改造点は、逆伝播を求めるメソッド “backword” を追加したこと、結果を観察する目的で「重み」W の初期値をガウス分布で与える代わりに 0.5、0.5、0.5 という定数の初期値を与えたこと、前述の通り2乗和誤差の係数 0.5 を忘れていたので追加したことだ。

画面上から Anaconda Prompt にコピー＆ペーストできるはずである。ただし実行にはch01～ch08 のいずれかをカレントディレクトリにしている必要がある（『ゼロから作るDeep Learning』の読者にしか通じない注釈）。

import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import sigmoid
class Perceptrn:
    def __init__(self):
        self.W = np.array([0.5, 0.5, 0.5])
        self.dW = np.zeros(3)
        self.z1 = None
    def predict(self, x):
        return x[0]* self.W[0]+ x[1] *self.W[1] + self.W[2]
    def loss(self, x, t):
        self.z1= sigmoid(self.predict(x))
        out = 0.5*(self.z1-t)**2
        return out
    def backward(self, x, t):
        dZ1 = (1-self.z1)*self.z1
        dZ2 = (self.z1-t)*dZ1
        self.dW[0] = dZ2*x[0]
        self.dW[1] = dZ2*x[1]
        self.dW[2] = dZ2
        return self.dW

このクラスの動作を確認するために、次の準備を行う。

from common.gradient import numerical_gradient
pct = Perceptrn()
print("W = " + str(pct.W))
f = lambda w: pct.loss(x, t)

x, t =(np.array([0, 0]), 0) 

クラス “numerical_cradient” のインポートは、数値微分との結果の比較のため。

x は入力データ、t は教師データである。

print("p = " + str(pct.predict(x)) )
print("l = " + str(pct.loss(x,t)))
print("dW(n.g.):"+ str(numerical_gradient(f,pct.W)))
print("dW(b.p.):"+ str(pct.backward(x, t)))

“p” は推定値、“l” は損失、“dW(n.g)” は数値微分により求めた値、“dW” は逆伝播法により求めた値である。

実際に実行させてみたスクリーンショットを以下に示す。

x と t の組み合わせをいろいろ変えながら上の4行を貼り付け実行して、結果を確認する。下図に示すのはORゲートの実行結果である。

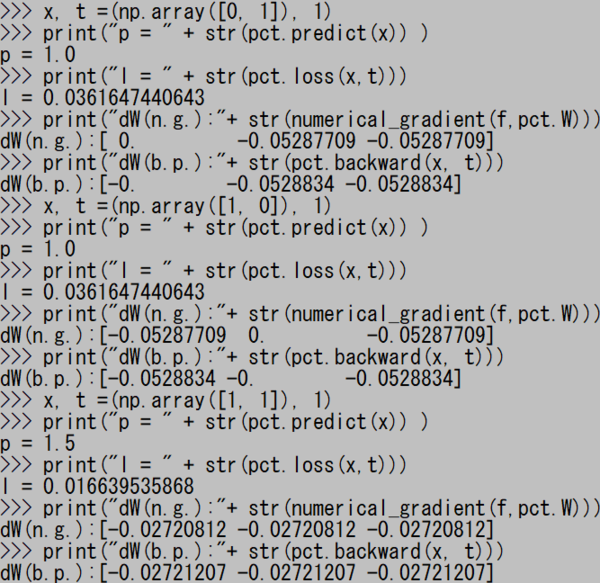
数値微分法で求めた値と、誤差逆伝播法で求めた値が、小数点以下5桁のレベルで一致しているということは、大きな間違いはしていないということだろう。

ただし「動けばいい」というつもりで作ったスクリプトなので、「その１」に書いた通りテキスト著者の斎藤さんや、Python のプログラミングに慣れた人だったら、ぜってーこんな書き方はしないだろうとも思う。

この項続く。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装