O'REILLY『ゼロから作るDeep Learning』5章誤差逆伝播法は見かけに反して意外な難関だった（その4：完結）

O'REILLY『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』（以下 “テキスト”）読者限定対象の、何度目かのシリーズの最終回です。

前回はシグモイドと2乗和誤差の誤差逆伝播法の実装について書いたが、テキスト5章のクライマックスは、続くAffineレイヤとSoftmax-with-Lossレイヤの実装のくだりなんじゃないかと思う。テキスト全体でも白眉と言えるんじゃないだろうか？ 実際、著者はSoftmax-with-Lossレイヤに関しては、巻末に10ページにわたる付録を設けて丁寧な説明を行っている。特別扱いしているのだ。

しかしこのテキストの例にもれず、Affine／Softmaxレイヤの実装の説明が終わると、いきなりニューラルネットワークへの逆伝播法の実装が始まる。難易度が断崖絶壁のように…ってこのフレーズを繰り返すのは何度目だ？

そこで今回は、自分自身に与える演習問題として、テキストP110の形状2×3の重みだけを持つ簡単なニューラルネットワークについて、逆伝播法で勾配を求めてみた。

スポンサーリンク

まずは計算グラフを描いてみた。そして、逆伝播の矢印を描き足そうとして、驚愕した。なんだこれは！？ 計算を付け加えるところが、2箇所しかないじゃないか？？

つまりAffineレイヤとSoftmax-with-Lossレイヤを、それぞれ一つの処理と見て、それらに対する逆伝播を計算すればいいということなのか？

P110（またはch04\gradient_simplenet.py）のコードを改造して、逆伝播の実装を試みた。以下に改造したコードを示す。いつもの通り、テキストのスクリプトが実行できる環境（GitHubからダウンロードしたスクリプトが実行できる環境）を構築している人なら、画面上からコピペでAnacondaプロンプトの対話モードに貼り付けて実行できるはずである。

import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import softmax, cross_entropy_error
class simpleNet:
    def __init__(self):
        self.W = np.array(\
        [[0.47355232, 0.9977393, 0.84668094],\
        [0.85557411, 0.03563661, 0.69422093]])
        self.dW, self.y = np.zeros([2, 3]), np.zeros(3)
    def predict(self, x):
        return np.dot(x, self.W)
    def loss (self, x, t):
        z = self.predict(x)
        self.y = softmax(z)
        loss = cross_entropy_error(self.y, t)
        return loss
    def backward(self, x, t):
        dZ = self.y - t
        self.dW[0] = dZ * x[0]
        self.dW[1] = dZ * x[1]
        return self.dW

テキストP110との相違点は、以下の通り。

テキストでは重み “W” はガウス分布で初期化しているが、数値を観察したいので、テキストP111と同じ値をnp.arrayで与えてみた。

Softmax-with-Lossの逆伝播を求める際に内部変数 “y” を使用するので、メンバ変数としてゼロで初期化してみた。

逆伝播を求めるメソッド “backward” は、逆伝播を与える式そのまんまである。ただしテキスト著者の斎藤さんや Python のプログラムに習熟した人は、ぜってーこんな書き方を…ってこれもしつこいですね、すみません。

上記クラスは、以下のように実行してみた。これも対話モードプロンプトに貼り付け可能のはずだ。

from common.gradient import numerical_gradient
net = simpleNet()
print(net.W)
x = np.array([0.6, 0.9])
p = net.predict(x)
print(p)
np.argmax(p)
t = np.array([0, 0, 1])
net.loss(x, t)
net.y - t

f = lambda W: net.loss(x, t)
numerical_gradient(f,net.W)
net.backward(x, t)

実行結果のスクリーンショットを撮ってみた。

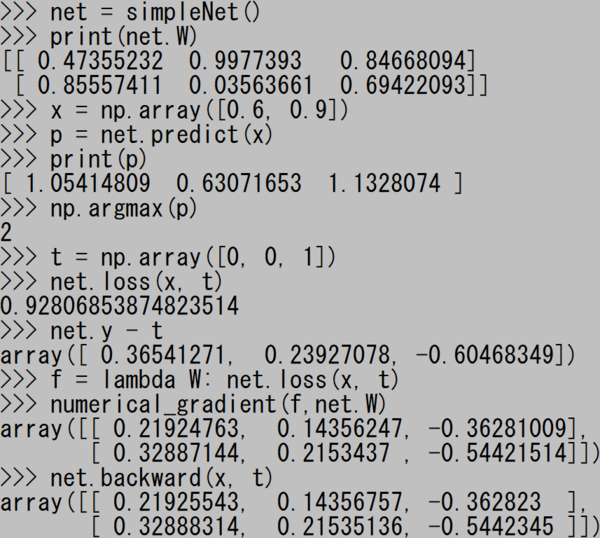
“numerical_gradient” すなわち数値微分で求めた値と、“backward” すなわち逆伝播法を用いた値が、小数点以下4桁目あたりまで一致していることが確認できた。

　　　＊　　　　　　　＊　　　　　　　＊

これがどれだけすごいか、これによって、どれだけ計算が節約できるかを可視化するため、前回に続いて今回もExcelで同じことをやらせてみた。前回に比べてシートが大きくなったので、スクショは2分割で示すが、一枚のシート上に作成したものである。

まずは左半分。

セル【B1:C1】の “入力 x” 、【F2:H3】の “重み W”、【F6:H6】の “教師 t” 、それに【C5】の数値微分を計算するための微小量 “h” は、数値の手入力である。

Softmax-with-Lossの出力を求めるまでの手順を説明する。

推定値 “p” を計算するセル【K2】には、数式「=$B2*F$2+$C2*F$3」を入力して 【L2:M2】にドラッグでコピーしている（絶対参照を使用しているのは、数式をコピーするためである）。

exp(p) を計算するセル【K5】には、数式「=EXP(K2)」を入力して 【L5:M5】にコピーしている。そのまんまというやつだ。

ソフトマックスを計算するセル【K8】には、数式「=K5/SUM($K$5:$M$5)」を入力して 【L8:M8】にコピーしている。セル【K5】の数式を「そのまんま」というのであれば、こちらも「そのまんま」と言える。

そしてセル【M10】で、数式「=-1*LN(F6*K8+G6*L8+H6*M8)」によりSoftmax-with-Lossの出力値を計算している。

次に、逆伝播による “dW” の計算である。

“y － t” を計算する計算するセル【K13】には、数式「=K8-F6」を入力して 【L13:M13】にコピーしている。くどいけど、これも「そのまんま」だ。

最後に “dW” を計算するセル【K16:M17】であるが、【K16】には数式「=K13*$B$2」を、【K17】には「=K13*$C$2」を入力し、それぞれM列までコピーしている。これがテキストP147～に言う「Affineレイヤの逆伝播」に相当する（はず）。

続いて右半分。同じことを数値微分でやろうと思ったら、これだけの手間が必要となるのだ。

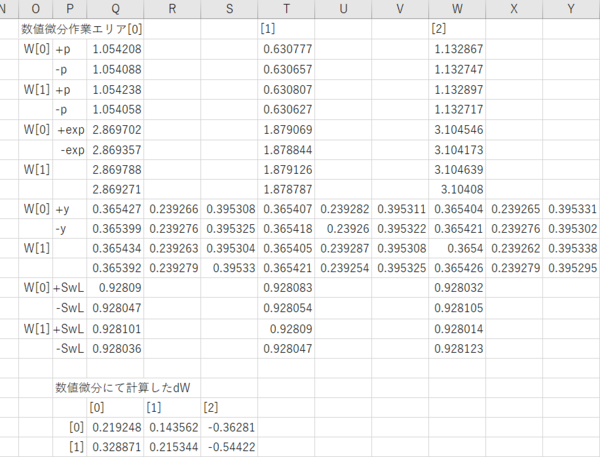
全部説明するのは大変なので、重み “W[0][0]” についてだけ述べる。

セル【Q2】には「=B2*(F2+$B$5)+C2*F3」に相当する数式を、【Q3】には「=B2*(F2-$B$5)+C2*F3」に相当する数式を、それぞれ入力している（「相当する」と書いたのは、実際に作成したシートでは、手数を節約できないかと絶対参照を指定したり指定していなかったりするため）。微小量 “h” に相当するセル $B$5 を加算または減算した推定値 p[0] = x[0] × W[0][0] の値を計算しているのである。

セル【Q6】、【Q7】では、それぞれ 【Q2】、【Q3】の exp すなわち「=EXP(Q2)」「=EXP(Q3)」を計算している。

次がもっともややこしいところである。セル【Q10】には数式「=Q6/(Q6+L5+M5)」を、【R10】には「=L5/(Q6+L5+M5)」を、【S10】には「=M5/(Q6+L5+M5)」を設定している。

セル【Q11】には数式「=Q7/(Q7+L5+M5)」を、【R11】には「=L5/(Q7+L5+M5)」を、【S11】には「=M5/(Q7+L5+M5)」を設定している。

今回のエントリーの最初に掲げた計算グラフで言うと、真ん中あたりの「EXP」というノードから分岐した支線3本が上の方の「＋」というノードで合流し、「／」というノードを経て元の線と合流する部分に相当する。

セル【Q14】には数式「=-1*LN(F6*Q10+G6*R10+H6*S10)」を、【Q15】には「=-1*LN(F6*Q11+G6*R11+H6*S11)」を設定している。この両者の値により “dW[0][0]” を「=(Q14-Q15)/2/$B$5」として計算したのである。

ややこしいばっかりで益がないな。「はてなブログ」には Excel のシートを貼る機能はないのか？（ないない

いやマジExcelのシートくらいどっかにアップロードできるのであればアップロードして、間違ったことをやってないか誰か他人の目でチェックしてもらいたいのだが。

ともあれ、かくして誤差逆伝播法の採用で計算量を格段に減らしたことによって、パソコンとインタープリタの処理能力でもMNISTデータセットの機械学習が可能になったということなのだろう。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装