おそらくSNSの相互さんに数学好きの人がいるせいであろう、タイムラインに数学問題のポストがよく流れてくる。
数式計算の力業で解かなきゃならない問題は、解けても解けなくてもあまり感情が掻き立てられることはない。
エレガントに解ける問題が「めのこ」で解けると、爽快感を感じる。逆に解けそうな問題が解けないと、当然ながら悔しい。
なんつーか、「時間溶かし」だと思う。それを言い出したらSNS自体が根本的な「時間溶かし」に違いないが。
何日か前に、こんな問題が流れてきた。
元ポストがサルベージできなかったので、脳内再生したものである。この脳内再生という行為が曲者だった。
先にお断りしておきます。この図形はデフォルメしたものであり、実際の寸法では作図不能です。
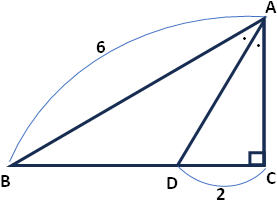
問:直角三角形ABCの斜辺ACが長さ6、直角でない角BACの2等分線と辺BCの交わる点をDとし、CDが長さ2である。三角形ABDの面積を求めよ。
出題者の「好きな問題」「通り一遍の公式の知識では解けない」というコメントともに「∠BAD=∠DACのときAB:AC=BD:DC」というヒント(?)がついていた。
私はまずヒントを見て「そうだったっけ? コレどうやって証明するんだ?」と考えてしまった。証明方法が思いつかなかった。
そうこうしているうち、鮮やかな正解を示したリプの一つが目に入ってしまった。
「△ABDをADで折り曲げると、CDは△の高さになる。よって△ABD=6×2/2
=6■」
あああああ!
数学の言葉を使うと、次のようになるであろう。
この図もまたオリジナルの問題ではなく私が記憶を頼りに再現したもので、実寸法による作図は不能ですからね。
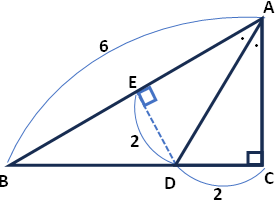
DからABに下ろした垂線の足をEとすると、△ACD≡△AED。よって△ABDは底辺長=6、高さ2。よって△ABD=6×2/2=6■
「∠BAD=∠DACのときAB:AC=BD:DC」使わねぇ! ミステリーでいうレッド・ヘリング(燻製イワシ=目くらまし)というやつか?
ときにこの公式も、けっきょく自力では証明できず、ぐぐってしまった。
こちらのサイトの後半に、鮮やかな証明が載っていた。
やはり補助線を使用しているが、補助線の引き方が上掲問題を解く場合とぜんぜん違っている。
ということは、やはり自力で解くには相当な困難が伴ったであろう。
うーん、悔しい。
追記:
△ABDと△ADCについて
AB,ACを底辺、ED=CDを高さと見て面積を計算しても
BD,CDを底辺、AC=ACを高さと見て面積を計算しても
結果が等しいことから
AB:AC=BD:CD (=△ABDと△ADCの面積比)
を証明することもできるそうです。なるほど!
追記おわり
ということで、ここまでを自ブログネタにしようと思って1枚目と2枚目の図形を作図しようとした。
先にお断りした通り、実寸法では作図できなかった。なんでだ??
以下、その探索である。ここまでは中学数学であったが、以下は三角関数や微分法など高校数学も使う。
弊ブログはアフィリエイト広告を利用しています
中心角θ、半径1の極座標グラフを描いてみた。明らかに最大値が存在することがわかる。書き込まなかったけど円周上の点がA、原点がB、直角がCである。
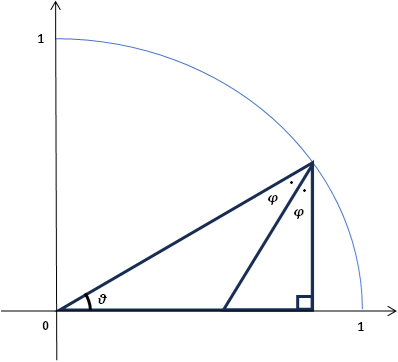
そうすると、最大値はいくつかという新たな図形問題が立ち上がった。
∠BACの2等分角をφと置くと、三角形の内角の合計は180°=πだから
φ=1/2(π-π/2-θ)=π/4-θ/2
ACの長さはsinθ、∠BACの2等分線とBCの交点をDとすると、
CD=sinθ・tanφ=sinθ・tan(π/4-θ/2)
残念ながら、私にはこれ以上の数式の簡略化はできなかった。使えそうな公式を、いろいろ当てはめてみてはいるのだけど。
個人的に、次にやることはExcelに突っ込んで数値的にいじくることだ。工学部出身者の発想だと思っている。
sinθとsinθ・tan(π/4-θ/2)のグラフを、0≦θ≦πの範囲で描いてみた。
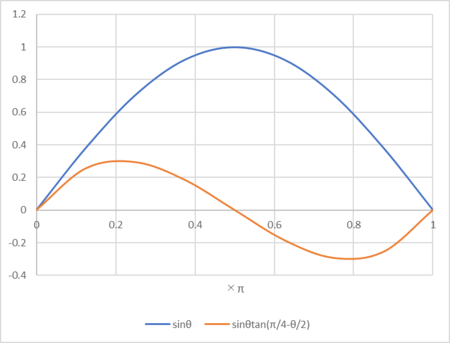
θ≒0.2π付近に0.3ほどの最大値があることが見て取れた。
最大値では(sinθ・tan(π/4-θ/2))のθによる微分値が0になる。
だが
(sinθ・tan(π/4-θ/2))'=cosθ・tan(π/4-θ/2)-sinθ/2cos^2(π/4-θ/2)
だから、解析的に微分値ゼロとなるθを求めるのは、よけいにやっかいそうだ。
よって、またしてもExcelで力業でゴリゴリ計算してみた。θ=0.66~0.67(約38°)付近に微分値ゼロすなわち極大値があり、そのときのCD長は約0.3のようだった。
| θ | CD長 | CD長微分値 |
| 0.64 | 0.2999 | 0.0289 |
| 0.65 | 0.3001 | 0.0178 |
| 0.66 | 0.3003 | 0.0068 |
| 0.67 | 0.3003 | -0.0041 |
| 0.68 | 0.3002 | -0.0148 |
| 0.69 | 0.3000 | -0.0255 |
ただし約38°という数値に、どのような意味があるのかは、よくわからない。
このあたり、解析的にθについて解ければ、いい問題になりそうなんだけどな。
もし解けるのであれば、誰かぜひ教えてください。
最初の図に戻って、AB=6であればCDはおよそ6×0.3=1.8を超えない。よってAB=6、CD=2という図形は描けなかったのだ!
とか何とかやっている傍らで、元ポストの検索もやっていた。
サルベージに成功した。スレッズだった!
あああああ! AB=15、CD=4だったのだ!
それなら図形が無理なく描ける!(15×0.3=4.5>4)
当然っちゃ当然だけど、やはり記憶はあてにならない。
だが、それなりに楽しませてもらったから、よかったことにしよう。こういう時間溶かしであれば、後悔はしない。
弊ブログはアフィリエイト広告を利用しています