もう一問、SNSに流れてきた中学数学レベルの図形問題である。
前回同様、やはり記憶に頼って問題を再現した。
今回は、前回と違って元ポストのサルベージに成功していない。
だが今回は、前回と違って図は描けた。
次図において?の角は何度か、という問題だった。
たしか「頭、ちゃんと動く?」みたいな煽りつきだった。
それで闘志を掻き立てられた。平たく言えばムカ来た。中学生かおまいは>自分
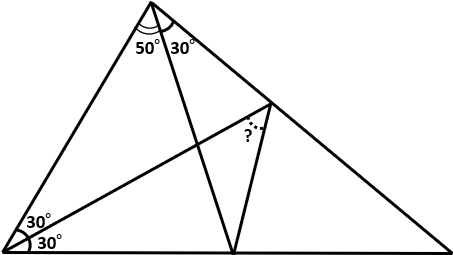
はじめ三角形の内角の和が180°であることを利用すれば、解けるのではないかと思った。
だが、いろいろやってみたが巧くいかなかった。
弊ブログはアフィリエイト広告を利用しています
結論のみ記す。円周角の定理を使うべきだったようだ。
説明のため、下図のように三角形の頂点それぞれにA、B、C、頂点A、Bから対辺に引いた線と対辺の交点にD、Eと記号をつける。
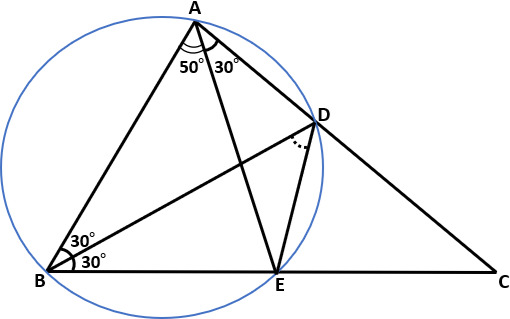
∠DAE=∠DBEだから、円周角の定理によりA、B、E、Dは同一円周上にある。
よって∠BDE=∠BAE=50° ? は50度■
いちおう作図した図形に分度器を当てて確認した。ぴったり50度だった。
間違ってないよね? (誰に訊く?
しかし、今回もまた新たな問題が立ち上がった。
この問題の場合、30°という同じ角度が多く登場することが手掛かりになった。
しかし、もし角度が違っていたら、どうやって解くのだろう?
例えば∠DBC=25° としても、同様の図は作図でき、同様の角度を求める問題が作成できるだろう。
そうすると円周角の定理は使えないし、詳述はしなかったが「三角形の内角の総和=180°」を利用してもこの問題と同様、巧くいかなさそう。
今後の研究対象としなければ。
追記:
自作した図でGoogle画像検索したところ、同一ではないが類題として「ラングレーの問題」「フランクリンの凧問題」と名前のついた一連の問題が表示された。
制約条件のある問題だが、それでも難易度高かった。
一般的な問題に対しては、三角関数やベクトルに頼るしかなさそうだ。
弊ブログはアフィリエイト広告を利用しています