椅子の脚で支柱が多角形の中心から頂へ放射状に延びる形状は意外にも最短ではなく特に正五角形では見慣れない形になる（その１）

目次

（その２）

• 正五角形のシュタイナー木
• 正五角形を外心と頂点で分割した三角形のシュタイナー木

（その３）

• 正五角形の第三の例
• 正六角形の二種類のシュタイナー木

スポンサーリンク

まえがき

何年か前に、椅子の脚の支柱は5本であることが多い理由について考察したエントリーをアップしたことがある。ただしネットでちょっと検索する限りでは、同じようなことを言っている人はあまり見当たらないのだが。

www.watto.nagoya

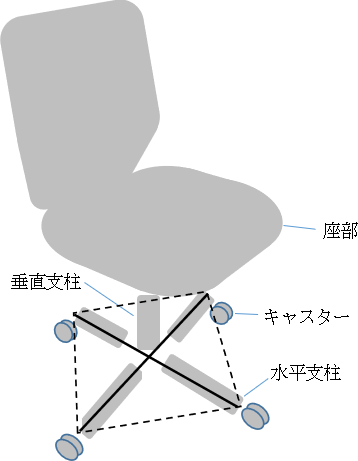
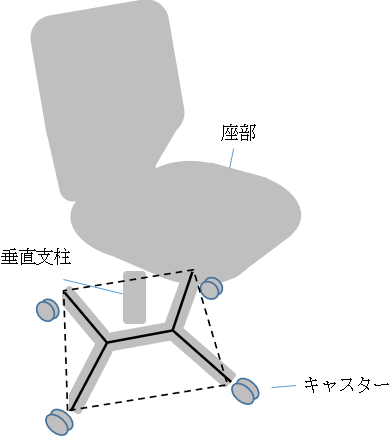
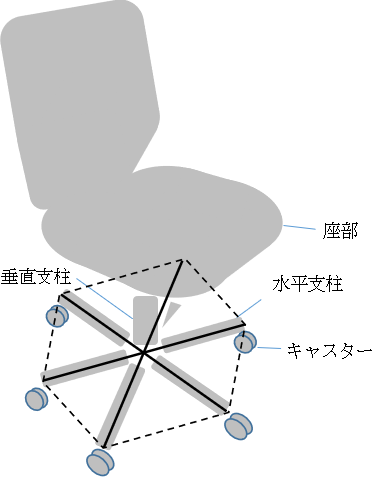
これがきっかけで、面白そうなことに気がついた。オフィスチェアの多くは、床に垂直な支柱が、床に平行な5本の支柱に放射状に分岐し、正五角形の頂点付近のキャスターで椅子を支える構造になっている。

言葉で説明するとわかりにくいので、イラストで示すとこんな感じ。左側が椅子を斜めから見たシルエット、右側が水平支柱だけを上から見た図のつもりだ。

うちのブログでは、結論を先に簡潔に述べることができる場合は、できるだけそうすることを心がけている。

今回も結論を先に述べる。

水平支柱の中心線のトポロジーとして、次のような形状を採用する。

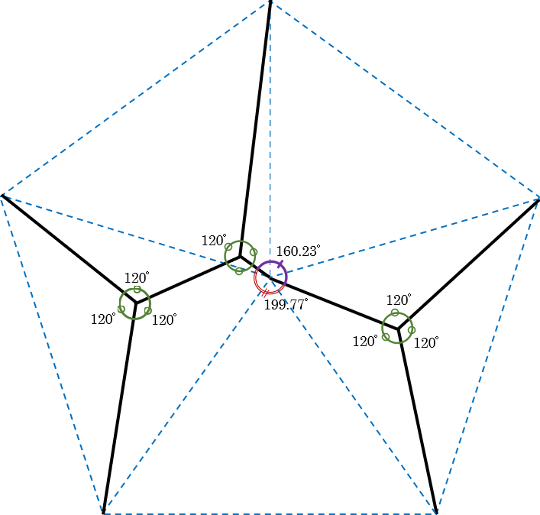
幾何学では、多角形の頂点のような複数の点を結ぶ線分長の合計を最短とする経路を「シュタイナー木」と呼ぶ。

線分が3本に分岐するとき線分の成す角がすべて120°となる場合を「フェルマー点」と呼ぶ。多角形の内部における分岐点がすべてフェルマー点である場合、頂点とフェルマー点を結ぶ形状はシュタイナー木を与えることが知られている（証明は後述）。

上図はそのシュタイナー木を2つ組み合わせた形状になっている。

追記：

すみません、「シュタイナー木」の定義がわかりづらかったので、この段落を書き改めました。

なお後半の「頂点とフェルマー点を結ぶ形状はシュタイナー木を与える」というのは正確でない模様ですが（「その３」参照）、結論が下せないのでとりあえずそのままにします。

追記おわり

水平支柱にこのような形状を採用すると、水平支柱の中心線の長さの合計で比較した場合、正五角形の中心と頂点を放射状に結んだ長さの合計を1とすると約0.928、すなわち約7.2%の短縮になるのだ。

線対象すなわち鏡像を採用しても、同じ結果が得られる。

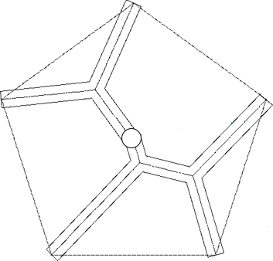
数学が得意な人は、これだけの説明でも「ははぁ」と察してもらえるんじゃないかと思う。数学が得意でない人にも楽しんでもらえないかと、これから多分エントリー3回分くらいかけて、のんびりゆっくり説明したいと思う。ただし三角関数だけは使用します。Windows アクセサリの関数電卓で計算できる範囲です。

詳しいことを早く知りたいという人がいるかも知れないので、元ネタへのリンクを貼っておきます。

astamuse.com

フェルマー点が最短経路を与える証明

あとで必要になるので、シュタイナー木が多角形の頂点を結ぶ線分長の合計を最短にする証明を、三角形の場合のみ示す。

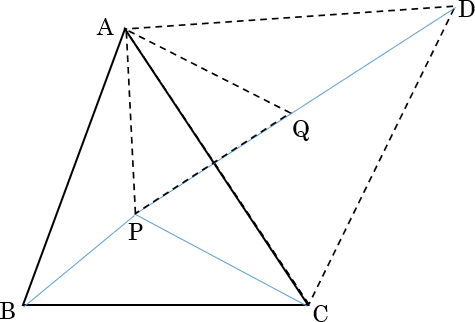
上図の三角形ABCにおいて、三角形の内部にある点を P とし、この点 P を、A を中心として反時計回りに 60°回転させた点を Qとする。

また頂点 C を、A を中心として反時計回りに 60°回転させた点を D とする。

三角形 APQとACD は正三角形となる。

三角形 APC と AQD は2辺とその間の角がそれぞれ等しいので合同となり、PC = QD。

よって
AP + BP + CP = BP + PQ + QD ≧ BD

等号が成立するのはB、P、Q、Dが一直線上にあるときで、そのとき
∠APB = 180°− ∠APQ = 120°

∠APC = ∠AQD = 180°− ∠AQP = 120°（証明終わり）

∠APB = ∠APC = ∠BPC = 120° となる P を三角形ABCのフェルマー点と称し、最大角が 120°未満の三角形にただ1つ存在する。

つかもともとシュタイナー木とは複数の点を結ぶ線分の合計が最短となる形状を言うのだが、三角形の内部にフェルマー点が存在する場合、フェルマー点と各頂点を結ぶ線分がシュタイナー木を与えるのだ。
120°以上の最大角を有する三角形においては、三角形内部にフェルマー点は存在せず、最大角を挟角とする三角形の2辺が、三角形の頂点を結ぶ最短の形状すなわちシュタイナー木となる。

こちらも元ネタへのリンクを。

mathtrain.jp

四角形以上の多角形においても内部にフェルマー点が存在することがあり、その場合は多角形内部の分岐点がすべてフェルマー点である経路がシュタイナー木すなわち多角形の頂点を結ぶ最短経路になるが、証明は省略する。

追記：

要検証なので抹消線を入れました。

追記おわり

水平支柱が四本である場合

椅子の脚が正方形の頂点に向けて四本に分岐している場合を計算してみる。

水平支柱を上から見たとき、水平支柱の中心線は実線のような形状になる。

正方形の1辺を1とすると、中心線の長さの合計は

√2 × 2 ≒ 2.828

である。

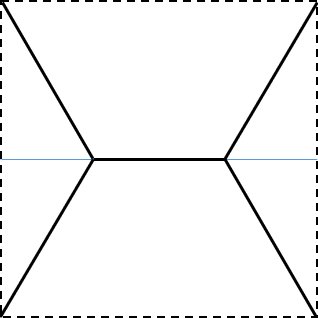
水平支柱の形状を、中心線がシュタイナー木になるように変更してみる。

水平支柱を上から見たとき、中心線は実線のような形になる。

分岐点（フェルマー点）から頂点までの線分の長さの和は

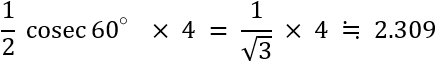
分岐点同士を結ぶ線分の長さは

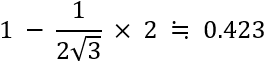
よって中心線の長さの合計は、2.309 ＋ 0.423 で約2.732。

2.732 ÷ 2.828 = 0.966 だから、中心線の長さの合計で比較した場合、約3.4％の短縮となる。

スポンサーリンク

水平支柱が六本である場合

次に、椅子の脚が正六角形の頂点に向けて六本に分岐している場合を計算してみる。

水平支柱を上から見たとき、水平支柱の中心線は実線のような形状になる。

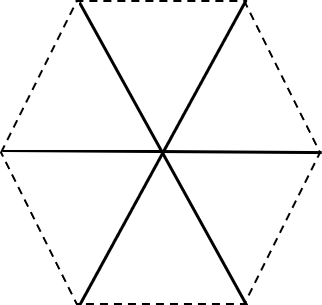
頂点と頂点を結ぶ線分は6つの正三角形を構成する。

正六角形の1辺を1とすると、中心線の長さの合計は 6。

やはり中心線がシュタイナー木になるように変更してみる。

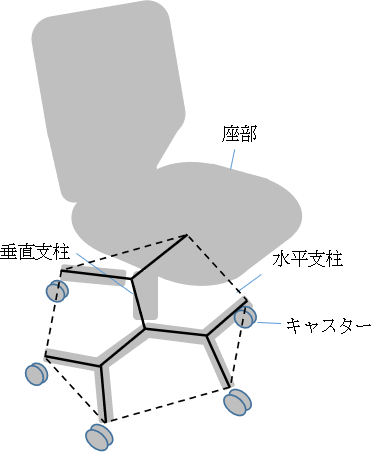
中心線は実線のような形状になる。

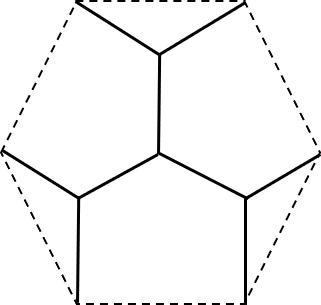
この場合、正六角形の中心からの分岐点（フェルマー点）までの線分の長さ、および各分岐点から各頂点までの線分の長さは全て等しく

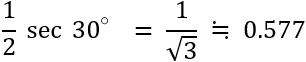
よって線分の長さの合計は

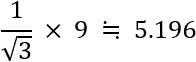
5.196 ÷ 6 = 0.866 ということで約13.4％の短縮となる。

13.4％の短縮って、かなり大きくないですか？

追記：

すみません、「その３」で述べるように、この形状を「シュタイナー木」と呼ぶのは誤りでした。すべての頂点を結ぶもっと短い経路が存在しました。ですが「その３」で言及し検証する必要上、今はこのままにします。

追記おわり

では最もポピュラーな正五角形の場合はどうなるかというと、興味深い形状がつぎつぎと現れるのだが、長くなるので一旦ここで稿を改める。

「その２」はこちら。

www.watto.nagoya

スポンサーリンク