椅子の脚で支柱が多角形の中心から頂へ放射状に延びる形状は意外にも最短ではなく特に正五角形では見慣れない形になる（その３：完結）

目次

（その１）

• まえがき
• フェルマー点が最短経路を与える証明
• 水平支柱が四本である場合
• 水平支柱が六本である場合

（その２）

• 正五角形のシュタイナー木
• 正五角形を外心と頂点で分割した三角形のシュタイナー木

（その３）

スポンサーリンク

正五角形の第三の例

ようやく「その１」冒頭で述べた形状の導出に入る。

正五角形の各辺、および頂点と中心（外心）を結ぶ線分によって構成される5つの二等辺三角形について、下図のように三角形一つと、三角形二つを組み合わせた四角形に着目し、それぞれのシュタイナー木を組み合わせるのだ。

上図右側の三角形（背景を黄色で着色）については、前回「その２」の考察と同じなので省略する。

左側の三角形2つを組み合わせた四角形（背景を薄桃色で着色）につきシュタイナー木を構成してみる。

正五角形の一辺の長さを1とし、二辺が交わる点を原点、右側の二等辺三角形のもう一つの底角の座標を (1, 0) とする。

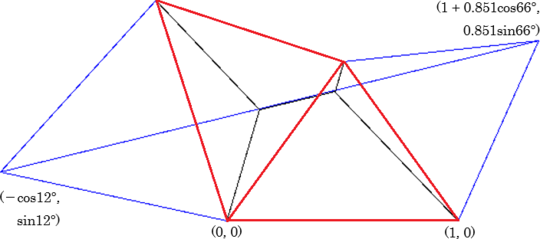
この座標を用いて、四角形のシュタイナー木を構成するためのフェルマー点の座標を求めるのであるが、計算はこれまでと比べてやや煩雑である。

いらんことを言うと、興が乗ると多少の計算の煩雑さは苦にならなくなるものです。ですが読者の皆さんには、次の「スポンサーリンク」の直前に計算結果を置きましたので、そこまで読み飛ばすことをお勧めします。

「その１」で、シュタイナー木が多角形の頂点を結ぶ線分長の合計を最短にする三角形の場合の証明を紹介した。その時と同様、補助線として正三角形を用いる。

すなわち、左側の二等辺三角形の底辺（すなわち正五角形の一辺）を一辺とする正三角形と、右側の二等辺三角形の右側等辺（すなわち正五角形の重心から頂点に引いた線分）を一辺とする正三角形を描き加える。

すると左側のやや大きい正三角形の、左端の頂点の座標は

(－cos12°,sin12°) ≒ (－0.978, 0.208)

右側のやや小さい正三角形の、右端の頂点の座標は

(1 + 0.851 cos 66°, 0.851 sin 66°) ≒ (1.346, 0.777)

となる。

それぞれの正三角形の頂点を結んだ補助線と、x 軸のなす角 θ を計算する。この θ を手掛かりに、必要な数値が次々と計算できるのである。

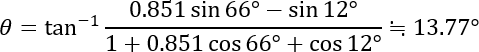
下図のように、フェルマー木を構成する線分を p ～ t 、四角形とフェルマー木の各部位のなす角度を α ～ δ と名づける。

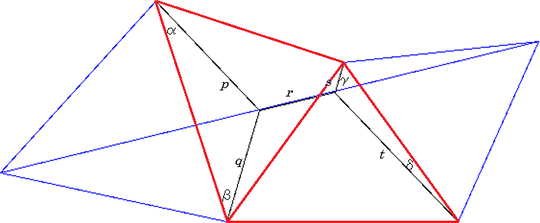
α ～ δ の値は、以下のように求められる。

α = θ＋12° ≒ 25.77°

β = 60°－α ≒ 34.23°

γ = β＋18° ≒ 52.23°

δ = 60－γ ≒ 7.77°

線分 p、q については

p sin α = q sin β
p cos α ＋ q cos β = 1

という連立方程式を解いて

p ≒ 0.6495，q ≒ 0.5020

s、t については

s sin γ = t sin δ
s cos γ ＋ t cos δ = 1/2 cosec⁡ 36° ≒ 0.851

を解いて

s ≒ 0.1328，t ≒ 0.7764

r については

シュタイナー木の左側のフェルマー点の座標は
(q cos(108°－β), q sin(108°－β)) ≒ (0.1403, 0.4820)

右側のフェルマー点の座標は

(1－t cos(54°－δ), t sin(54°－δ)) ≒ (0.4629, 05607)

r ≒ √((0.4629-0.1403)^2 + (0.5607-0.4820)^2 ) ≒ 0.3321

四角形のシュタイナー木の長さの合計は

p + q + r + s + t ≒ 0.6495 + 0.5020 + 0.3321 + 0.1328 + 0.7764 ≒ 2.393

三角形のシュタイナー木の長さは「その２」で計算したように

0.577 × 2 + 0.400  = 1.554

よってシュタイナー木全体の長さは

2.393 + 1.554 ＝ 3.947

すべての頂点を正五角形の外心からの放射状の枝で結んだ場合の長さの合計は、これも「その２」で計算したように

0.5 sec 54° × 5 ≒ 0.851 × 5 = 4.253

よって

3.947 ÷ 4.253 ≒ 0.928

すなわち約7.2％の短縮となる。

スポンサーリンク

実現可能性はひとまず措くとして、この形状を採用した椅子の脚のイメージを再掲する。

「その１」～「その３」の結果を、表にまとめてみた。

	(1)変形後	(2)放射状	(1)÷(2)	短縮率
正方形	2.732	2.828	0.966	3.4%
正五角形1	3.892	4.253	0.915	8.5%
正五角形2	3.953	4.253	0.931	6.9%
正五角形3	3.947	4.253	0.928	7.2%
正六角形	5.196	6	0.866	13.4%

ちなみに正三角形のシュタイナー木は、外心と頂点を放射状に結んだ線と一致する。

正七角形以上は、頂点の角度が120°を超えるため、内部にフェルマー点を持ち得ない。従って、一辺を除いて他の辺をすべて結んだ形状が、シュタイナー木を与える。 

 今回のシリーズには、多くの閲覧とブックマークをいただき、感謝しています。ありがとうございました。

もちろん幾何学的な好奇心を動機として書いたエントリーですが、椅子デザイナーさんがヒントにしてくれないかという微粒子レベルの期待はあります。 

「その１」のコメント欄で、id:sierraromeo さんから「カンチレバーチェア」というものを教えていただきました。ありがとうございました。こんなのです。

ダイニングチェア カンティレバーチェア カンチレバーチェア 椅子 2脚 イスのみ (ホワイト)

カンティレバーチェア or カンチレバーチェアという名称は知らなかったのですが、この形状の椅子には、どこかで腰かけた記憶があります。

「カンティレバー」すなわち「片持ち梁」というのが構造設計ではタブーに近いということは、かすかにどこかで聞いた記憶がありますが、それをあえて採用するのがデザイナーズファニチャーの世界というものかも知れません。

シュタイナー木に基づく形状を椅子の脚に採用するメリットとしては、材料費の節約という意味では、あまりメリットがないように思います。なぜなら手持ちのオフィスチェアをいくつか確認した限り、たぶん重みを増して安定度を増加させる目的だと想像しますが、材料を多めに使用しているように思われたからです。安全率を大きめにとる、というやつです。

なおこの椅子の場合、溶接ではなくダイキャストで一体成形されているようです。

では総延長を減らすことによるメリットは何かというと、脚が床を覆う面積がその分だけ小さくなることで、それに加えて、正五角形の場合では放射状の場合は中心角が鋭角だったのがすべての角が鈍角になることで、靴が挟まりにくくなるとか、消しゴムなど小物を椅子の下に落としたときに拾いやすくなるといったメリットがあるかも知れません。たいしたことはないですけど。

最大のメリットは、デザインの自由度が広がる可能性だと思います。現状のオフィスチェアは、ほぼ五角形放射状のワンパターンなので。ただしブコメなどでご指摘をいただいた三次元的構造や負荷分散といった問題については、私は全く知識を欠くため専門家の力を借りるしかありません。どなたか専門家が興味を持ってくださることを期待するしかありません。

正六角形の二種類のシュタイナー木

問題と言えば、むしろ幾何学の観点から、やっかいな、それゆえ興味深い問題が立ち上がるように思われました。

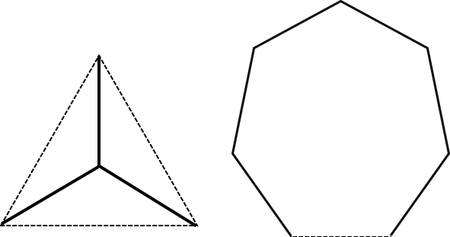
正六角形のシュタイナー木として、「その１」で次の形状を示しました。

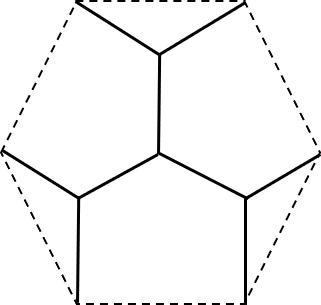
しかし「google:正六角形のシュタイナー木」で検索すると、次図に示す形状がヒットします。

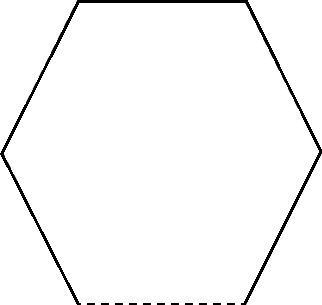
しかも、この形状のほうが、線分の総延長が短いのです！

正六角形の一辺を1とした場合 5 であることは容易にわかり、「その１」で計算した 約5.196 より明らかに小さいのです！

（もともとシュタイナー木という語の定義は「複数の点を最短の総延長で結ぶ線分のセット」ですから、両方をシュタイナー木と呼ぶのは誤りですが、「その１」で2つ上の図を正六角形のシュタイナー木と呼んでしまったので、本エントリーではこれで押し通します）

これは、どう解釈したらよいのでしょうか？

「頂点とフェルマー点を連結した線分は、多角形のシュタイナー木（すなわちすべての頂点を結ぶ線分の最短の総延長）を与える」というのは、局所的にしか正しいと言えないということでしょうか？

もし両者の総延長が等しくて、しかも変形によって一致が示せるとでもいうのであれば、わかりやすいというか気持ちがいいかも知れません。しかし、どう考えてもそうは見えないのです。

数学では、問題の意味がわかりやすく、なおかつ難解な問題が「よい問題」だと言われます。二種類のシュタイナー木がどのような関係にあるか解釈づけるのは、ひょっとしたら数学でいう「よい問題」になりうるかも知れません。

ですが、どこからどう手をつけたらいいのか、いまのところ見当がつかないでいます。

「トポロジー的に相異なる2種類以上のシュタイナー木を有するのは、正六角形が唯一の例か？ それとも他にあるのか？」という問題も、提唱できるかも知れません。

（繰り返しになりますが、長さが異なるシュタイナー木が2種類以上あるという表現は定義に反し不正確です。「すべての頂点を頂点自身かフェルマー点のみで連結する形状が2種類以上ある」と表現するべきでしょうか？ より正確な表現も含めて、目下、検討中です）

シュタイナー木を用いた椅子の脚の特許は、ざっと検索した限りでは いつも元ネタとして示している一件 のみのようですが、電気回路や通信経路の分野では何件かヒットします。すなわちシュタイナー木はすでに実用的に利用されている可能性があり、こうした研究にはひょっとしたら実用的な意義があるかも知れないのです。

私の手に余りそうではありますが、まずは先行研究の調査を、ゆるゆると始めようかと思っています。

追記：

わわわわわ、ネットでこんな図形を見つけた。

正六角形の中に、相似で外心が同じ正六角形を描き、外側の正六角形の頂点と内側の正六角形の頂点を連結し、内側の正六角形の辺を連結したものである。

こうすると、内側の正六角形の頂点は、すべてフェルマー点となる。

このような図形は、外側の正六角形と内側の正六角形がどのような相似比であっても描けるので、正六角形のすべての頂点をフェルマー点のみで結んだ図形は無数にあることがわかる。

また、この図形は、相似比に関わらず線分の長さの合計が外側の正六角形の辺の長さの合計に等しくなるという、ちょっと面白い性質を持つ（外側の正六角形の頂点と内側の正六角形の頂点を結ぶ線分のひとつにつき、下図のような補助線を引くと、平行四辺形の対辺が等しいことにより容易に証明できる）。

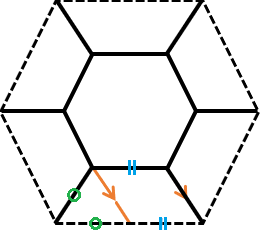
他にもいろんな性質がありそうだ。

ただし、どうもフェルマー点という道具だけを使って正多角形のシュタイナー木問題を解決するのは不可能らしいことは、わかった。

スポンサーリンク