O'REILLY『ゼロから作るDeep Learning』3章 ニューラルネットワークで7セグメントならぬ4セグメントLEDを認識させてみた

何年か前から半年に1冊のペースで専門書を読もうとしている。専門書と言っても、大学1～2年くらいの難易度だが。

今読んでいるのは『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』である。気づいたことをエントリーにしているのだが、気づいたら前回の記事から3ヶ月も経ってしまっていた。

watto.hatenablog.com

3章でニューラルネットワークというのを導入する。早い話が行列演算である。その他いくつかの準備をすると、次はいきなり「MNISTデータセット」という手書き数字のテストデータを認識させる。

ここが、とてもわかりにくかった。プログラム言語 Python で書かれたコードがGitHub からダウンロードでき、演算中のデータが好きなところでダンプできるので、テキストには載っていないテストルーチンを追加して随所でデータをダンプしたりしながら、ようやく何をやっているのか理解した…つもり。

理解するって、どういうことなのかね？ しばしば言われることだが、「理解する」ということ自体が、最も理解しがたいものの一つなのかも知れない。

本当に理解しているかどうかを確認するために、練習問題を作って解いてみるというのは、よく行われる手段だと思う。上掲書では2章でANDゲート、ORゲート、NANDゲートという論理回路をパーセプトロン（これもぶっちゃけ行列演算である）で実現して、そこからいきなりMNISTデータセットにチャレンジする。難易度が断崖絶壁のように変化する。

中間はないんかい！？ ってことで、難易度はそうとうに下がるが、7セグメントLEDをニューラルネットワークで認識させられないかと考えた。

手をつけてみたら、7セグメントLEDでもかなり複雑なことになりそうだった。それでさらに難易度を下げて、4セグメントLEDというのを考えることにした。

4セグメントLEDというのは、こういうものである。そんなものがあるかどうか知らないけど、私が考えたのだいいじゃないか。

名前の通り4つのLEDから構成される。一番上が最下位ビット、時計回りに上位ビットに対応にしてゆくとする。

上掲図の一番上、すなわち全部点灯した状態（1, 1, 1, 1）を「0」とする。

真ん中の（0, 0, 1, 0）と一番下の（1, 0, 0, 0）は、いずれも「1」とする。「1」に二通りの表現があるというのが、いわばミソである。

話を単純にするため「2」～「9」は表現不能とする。「7」は、なんとかなりそうな気もするが諦める。

これを、テキストP84～86でいうところの「機械学習」ではない「人の考えたアルゴリズム」で、認識させようというのだ。

スポンサーリンク

まずはテキストP60～61「第1層1番目のニューロン」を改造してみた。コードはPythonの対話モードに貼り付けが可能のはずである。

import numpy as np
x = np.array([[1, 1, 1, 1],[0, 0, 1, 0],[1, 0, 0, 0]])
W1 = np.array([[0.3, -0.2, 1.1], [0.3, -0.2, -0.2],
    [0.3, 1.1, -0.2], [0.3, -0.2, -0.2]])
B1 = np.array([-1, -1, -1])
A1 = np.dot(x,W1) + B1

上記コードを行列で表現すると、こんな形になる。

変数 x は入力で、テキストの例は2入力だが3入力に改造した。1行目が「0」すなわちビットがすべて1のケースに対応する。2行目と3行目は、それぞれ1ビット目と3ビット目だけが1のケースに対応する。

W1は第1層目の重み、B1は第1層目のバイアスで、「0.3」「-0.2」「1.1」「-1」という数値は私が適当に考えた。1列目はビットがすべて1のときに限り、2列目と3列目は特定のビット1つだけが1のときに限り、正になるような数値の組み合わせであれば、何でもいいのだ。

　　　＊　　　　　　　＊　　　　　　　＊

続いてP61～62の「第1層目の活性化関数」に関しては、テキストのシグモイド関数ではなく、ステップ関数（P47）を採用してみた。今後、機械学習にもチャレンジしたいと思っている。その際にステップ関数ではうまくいかないかも知れないが、今は単純さ、わかりやすさを優先した。

関数の定義は、どこでやってもいい。

def step_function(x):
    return np.array(x > 0, dtype=np.int)

関数を使う前に定義されていればいいのだ。

Z1 = step_function(A1)

ここで print(A1)、print(Z1) でA1とZ1をダンプすると、こうなるはずである。

Z1が3×3の単位行列になってしまうのが、なんか気持ち悪い。つか「何をやってるんだろう」感がある。論理回路を使った方が早い。それはじゅうじゅう承知なのだが、将来の（と言っても5章だが）機械学習を見すえてパーセプトロンで論理回路を実現していることがキモなのだ。

　　　＊　　　　　　　＊　　　　　　　＊

続いてテキストP62～63「第1層から第2層への信号の伝達」を改造する。やりたいことは、Z1の2列目と3列目のORをとって1列にまとめたいだけである。つまり、どっちかが1だったら「1」ということだ。だがこの操作が、1層のニューラルネットワークだけでは不可能だから、多層のニューラルネットワークが必要となるわけだ。

遠回りで面倒なことをしている気がするが、あえてやってみる。くどいようだが後々の機械学習のためだ。

W2 = np.array([[1, 0],[0, 0.5], [0, 0.5]])
B2 = np.array([0, -0.2])
A2 = np.dot(Z1,W2) + B2
Z2 = step_function(A2)

W2は第2層目の重み、B2は第2層目のバイアスで、数値はテキストP27～28でパーセプトロンでORゲートを実現したときと同じものを、わざと使ってみた。

W2とA2を行列表現すると、こうなるはずである。

　　　＊　　　　　　　＊　　　　　　　＊

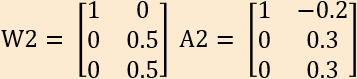
最後に出力層だが、テキストP63の identity_function ではなく代入を使ってみた。理由は単に面倒だったからだ。

y = Z2

これも行列表示。

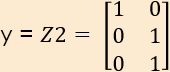
ただしこの結果を、続くテキストP63～の「ソフトマックス関数」に適応するのは、よろしくない。LEDの輝度を「0」と「1」のデジタルでやってしまったからだ。パーセントを用いれば面白いかも知れない。今回の場合は、P80で出てくる np.argmax(y, axis =0) というのを使うのがいいんじゃないかな。つまり行列の最大要素が△行目に出てくるとしたら、△というのが表示された数字だということで。

　　　＊　　　　　　　＊　　　　　　　＊

最後に、こんなこともやってみた。4セグメントLEDの2の4乗全部の組み合わせについて、上記コードを試してみたのだ。

x = np.array([[0, 0, 0, 0],[0, 0, 0, 1],[0, 0, 1, 0], [0, 0, 1, 1],
[0, 1, 0, 0],[0, 1, 0, 1], [0, 1, 1, 0],[0, 1, 1, 1],[1, 0, 0, 0],
[1, 0, 0, 1],[1, 0, 1, 0],[1, 0, 1, 1], [1, 1, 0, 0],[1, 1, 0, 1],
[1, 1, 1, 0],[1, 1, 1, 1]])

A1 = np.dot(x,W1) + B1
Z1 = step_function(A1)
A2 = np.dot(Z1,W2) + B2
Z2 = step_function(A2)
y = Z2

テキストP79流に行列サイズを表記してみる。

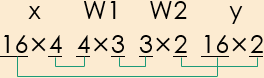
結果の y は 16×2の行列として得られる。1 が現れるのは（0, 0, 1, 0）、（1, 0, 0, 0）、（1, 1, 1, 1）に対応する行だけで、それ以外は全部 0 だった。これは期待した結果である。

追記：

この図解が必要なのだった。第1層と第２層のやっていることを論理回路で示す。

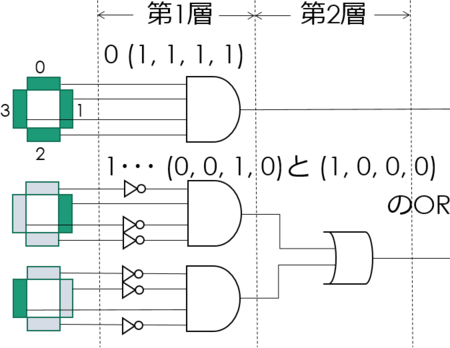
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装