O'REILLY『ゼロから作るDeep Learning』4章のクラスを使ったら4セグメントLEDどころか7セグメントLEDの機械学習ができた！（その2）

前回の記事 を書いた段階でも、他にもいろいろ気づきがあった。例えば『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』（以下「テキスト」）4.4 の勾配というのは、ベクトル解析でいう多次元の勾配と同じことだったのだ！ 

なんだか書いてみるとあたりまえのことだな。テキストP103で「勾配」という言葉が最初に出てきたときには、2変数の関数に対する勾配を数値微分によって求め、次の段階でP109で対象がニューラルネットワークに拡張されたため、気づくのが遅れた。ニューラルネットワークとしてはごく簡単な例とは言え、いきなり6変数（6次元）なのだ。それを自分で3変数（3次元）に引き下げて、遅まきながら「あっ、そうか」となった。ベクトル解析の授業で、6次元の例題なんてそうそう扱わないよね？ 

さらに言うと、数学（より狭くは幾何学）でいう「次元」と、プログラミング（より狭くは配列）でいう「次元」には、意味のズレがある。テキストP109のニューラルネットワークは6変数なので数学的には6次元だが、プログラミング的には2次元6要素（3×2要素）の配列なのだ。

これも言語化できてしまえば何と言うことはないが、「ナニガワカンナイカワカンナイ」状態のときには、じゅうぶん躓きの石の一つとなる。

スポンサーリンク

それはともかく、4セグメントLEDである。4セグメントLEDに関しては 5月21日付拙記事 参照。私がでっち上げたもので現実にそんなものはない。これを認識させるには2層ニューラルネットワークが必要となるのがキモである（前回のパーセプトロンは1層）。

そこで今度は、テキストP114～115にコードがある2層ニューラルネットワークのクラス “TwoLayerNet” を流用することにした。

とは言うものの、私はクラスという概念になじんでいるとは言えない。Python という言語においては、なおのことである。だからまずは、データと関数をバラバラに流用することにした。

今回示すコードも、 Anaconda Prompt に貼り付けて実行可能なはずである。

import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient
x = np.array([[1, 1, 1, 1],[0, 0, 1, 0],[1, 0, 0, 0]])
t = np.array([[1, 0], [0, 1], [0, 1]])
weight_init_std=0.01
W1 = weight_init_std * np.random.randn(4, 3)
W2 = weight_init_std * np.random.randn(3, 2)
B1, B2 = np.zeros(3), np.zeros(2) 

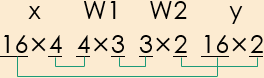
インポートは  “TwoLayerNet” と同じにし、入力データ “x” と教師データ “t” は numpy配列で与えてしまった。1層と2層の重みとバイアスは、サイズだけ指定して “TwoLayerNet” と同じ方法で与えた。

なんで1層と2層のサイズがこうなるかについては、5月21日付の拙記事より図のみ引用して再掲する。“y” は出力データである。

推定を行う関数は、クラス“TwoLayerNet” の “predict” メソッドと同じにした。つかそのままコピペした。

def predict(x):
    A1 = np.dot(x,W1) + B1
    Z1 = sigmoid(A1)
    A2 = np.dot(Z1,W2) + B2
    y = softmax(A2)
    return y

損失関数も、クラス“TwoLayerNet” の “loss” メソッドをそのまま流用した。前回の自作クラス "Perceptrn" では損失関数に二乗和誤差を使用したが、交差エントロピー誤差使用に変更したのは特に意味があってのことではない。

def loss(x, t):
    y = predict(x)
    return cross_entropy_error(y, t) 

認識精度を求めるメソッド “accuracy” は、今回は使わないので流用しなかった。

そしてパラメータの更新は、メソッド “numerical_gradient” を使う代わりに、今回も繰り返しコピペによって実行する。

その準備として、先に定義した損失関数 “loss” をラムダ式によって読み込む。実は Python のラムダ式というのを、まだよくわかっていないのは内緒。学習率 “leaning_rate” は0.1ではなく1.0としてみた。コピペ回数が減らせるかなというほどの意図である。

loss_W = lambda W: loss(x, t)
learning_rate = 1.0

そして以下を繰り返し Anaconda Prompt に貼り付けとなる。predict(x) は推定値の生データの表示、argmax（テキストP80）を噛ませたのは、前回のステップ関数と同様、ちょっとは結果が見やすくならないかなという工夫のつもりである。

関数 “numerical_gradient” は common\gradient.py からのインポートだ。これに学習率を掛けたものが、重みとバイアスの修正値となる。

predict(x)
np.argmax(predict(x), axis =1)
loss(x, t)
W1 -= learning_rate*numerical_gradient(loss_W, W1)
B1 -= learning_rate*numerical_gradient(loss_W, B1)
W2 -= learning_rate*numerical_gradient(loss_W, W2)
B2 -= learning_rate*numerical_gradient(loss_W, B2)

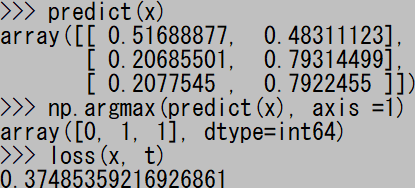
貼り付け一回目。下から3行が “array([0, 1, 1]…” となれば正解だ。

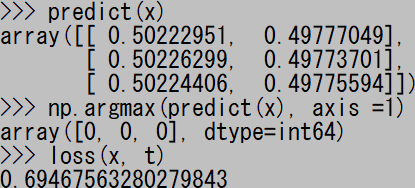
二回目。損失 “loss” の値が減少している。

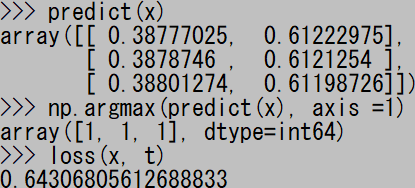
26回目。正解が出る直前。

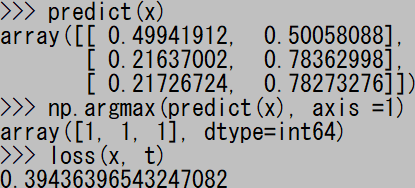
27回目にして正解が出るようになった。いつもだいたい30回貼り付けるまでには正解が出るようだ。

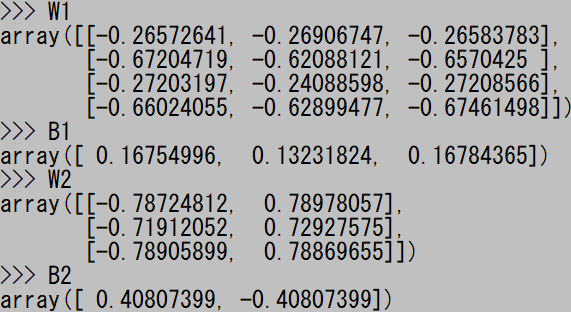
この段階で、1層目の重み “W1” とバイアス “B1”、2層目の重み “W2” とバイアス "B2" をダンプすると、興味深い値が表示された。

だいたいこんな感じ。ただし上に貼り付けたときとは別の試行である。

収束を確実にするため、念のためもう20回ほど、合計50回ほど貼り付けを繰り返した。これも別の試行だから初期値が違う。あのデータも採っとけばよかった、このデータも採っとけばよかったというのは、だいたいあとから気づくので。

ものは試しということで、その結果をダンプした値を基に、5月21日の「人の考えたアルゴリズム」の重み "W1"、"W2" とバイアス "B1"、"B2" を、次のように変更してみた。

common\functions.py からすべての関数をインポートしているので、ステップ関数 “step_function”（テキストP45）も使えるのだ。

x = np.array([[1, 1, 1, 1],[0, 0, 1, 0],[1, 0, 0, 0]])
W1 = np.array([[-0.31, -0.29, -0.30], [-1.11, -1.23, -1.20],
[-0.29, -0.28, -0.27], [-0.73, -0.77, -0.70]])
B1 = np.array([0.54, 0.70, 0.68])
A1 = np.dot(x,W1) + B1
Z1 = step_function(A1)
W2 = np.array([[-1.31, 1.31],[-1.51, 1.51], [-1.47, 1.48]])
B2 = np.array([1.15, -1.15])
A2 = np.dot(Z1,W2) + B2
Z2 = step_function(A2)

上記コードを Anaconda  Prompt に貼り付けて Z1、Z2 をダンプすると、次のようになった！

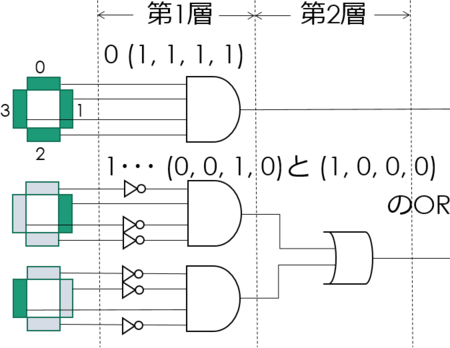
5月21日拙記事に示した係数を使用したときには、Z2 すなわち第2層の出力は同じ結果だったが、Z1 すなわち第1層の出力は単位行列みたいになったのだった。

画像のみ再掲。

これはこれで、興味深い研究対象を与えてくれるように思う。5月21日で決めた係数は、4セグメントLEDの表示のうち “0”、“1” に対応する以外の組み合わせについては、すべて「値なし」を返してくれた。だが今回の係数は、それらの組み合わせに対しては学習を行っていないので、おそらく誤った値を返してくるであろうことは、すぐに想像がついた。「値なし」を学習させるには、どうしたらいいんだろう。ちょっと知恵を絞らなければならない。

だがその前に、今回のスクリプトを作っていて、重要なことに気がついたので、そっちを先に試さなきゃと思った。

今回のスクリプトは、結局テキストP114～115の2層ニューラルネットワークのクラス “TwoLayerNet” の流用で事足りてしまった。ということは、せっかくのクラスをわざわざ崩さなくても、クラスに適切な引数を与えれば実行できるのではないかと思いついたのだ。

やってみたら、本当に実行できた！ そのことは今回のシリーズのブログタイトルに掲げ「その１」の冒頭でも結論から先に述べた通り。だが今回も長くなったので、ここでまた一旦エントリーを区切り、内容は次回で詳述することにする。

この項続く。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装