O'REILLY『ゼロから作るDeep Learning』5章誤差逆伝播法は見かけに反して意外な難関だった（その3）

前回の内容、すなわち「2章パーセプトロンによる論理ゲート」を誤差逆伝播法で機械学習するという自作の演習問題を解いてみた感想だ。

まずは、なぜ自分の書いたスクリプトが「動けばいい」というレベルにすぎず拙い、ということを繰り返したかという理由から。O'REILLY『ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装』（以下 “テキスト”）に掲載されているクラスは、前回使用した数値微分を求める “numerical_gradient” にしろ、6月26日付 および 7月1日付 記事で使用したMNISTデータセットの推定値を求める  “TwoLayerNet”  にしろ、目的以外の用途に使用しても立派に動作してくれた。私の書いたスクリプトでは、絶対そうはいくまい。

これは、たまたま動いたのではなく、あえてそう作ってあるのだと思う。例えば “numerical_gradient” のソースコードを見ると、for 文（“イテレータ” と言うのだそうだ）が多次元配列にも柔軟に対応できるような書き方になっている。「はぁ、Python ではこう書くのか！？」と思わずにはいられなかった。それ以前に、考えてみれば私は昔から汎用性の高いプログラムの書き方をするのが苦手だった。ナマの数値（“リテラル” とか “マジックナンバー” とか呼ばれる）を変数に置き換えるだけでも抵抗を感じるタイプなのだ。一言で言えばプログラミングの才能がないのだろう。

スポンサーリンク

そんなわけで、たったあれだけのスクリプトを書くだけでも、情けないほどの労力を消費した。どこでどう苦労したかを他人に説明するのは案外困難なものだが、他に躓きの石となった原因として、比較的言語化しやすいかなと思ったものに、次のようなことがある。

逆伝播を求める式は、簡略であるに越したことはない。だから Sigmoid レイヤの逆伝播を与える式は、順伝播における出力側の変数を用いて、次のように記述した。出力側というのは、丸印で示した計算ノードの右側ということだ。前回のエントリー に示した自作の計算グラフから取り出したものなので、変数名がテキストP146の図5-22と異なっているが、内容的には同一のはずである。

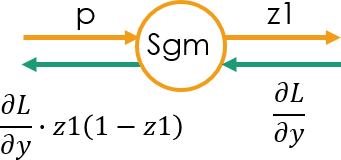
一方、2乗和誤差の逆伝播を与える式は、順伝播の入力側の変数を用いて記述した。入力側というのは、計算ノードの左側ということだ。テキストに全く同じものはないが、P132 の “z = t**2”、“t = x + y” についての逆伝播を示した図5-8が、内容的には似ているはずだ。

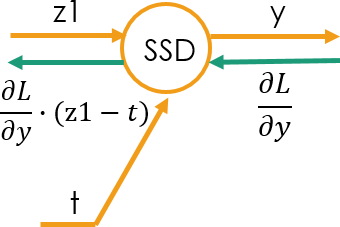
入力側の変数だろうと出力側の変数だろうと、クラスのインスタンス変数（内部変数）として保存することはいくらでも可能なので、使いやすいものを使えばよい。言語化してしまえばただそれだけのことだが、やってる最中は、「あれ？ オレ今何を計算してるの？」とわけわかんなくなることが、しょっちゅう起きたのだ。

また結果として、スクリプトに z1*(1 － z1)*(z1 － t) という内部変数 z1 の3乗を計算する式が現れた。「これなに？」てなもんで大変気持ち悪く感じたが、間違ってはいないはずだ（よね？

気持ち悪さを少しでも解消しようと思って、つかダメを押すようなつもりで、Excel で同じことをやってみようと思いついた。Excel を使えば内部変数の一覧化、可視化ができるはずだ。

事前の予想に反してこれも少なからず苦労したが、こんなものができたと結果のスクショを示す。

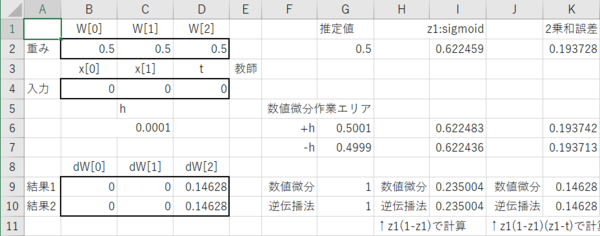
セル B2：D2（重み・バイアス）、B4：D4（入力データ・教師データ）、および h （数値微分用微小値）が入力データである。

以下、設定した数式を示す。

セル G1（推定値）：=B2*B4+C2*C4+D2

セル I1（Sigmoid）：=1/(1+EXP(-1*G2))

セル K2（2乗和誤差）：=0.5*(I2-D4)^2

そして、作業エリアでセル B2（：重み W[0]）、C2（：重み W[1]）、D2（：バイアス W[2]）のいずれかをそれぞれ ±h だけ変化させ、上掲式と同内容の計算結果の差を取ってセルG9、I9、K9の数値微分値とする。

一方、逆伝播法による値として、セル I10 に=I2*(1-I2)（z1(1-z1) に相当）、セル K10 に =I10*(I2-D4)（z1(1-z1)(z1-t) に相当）という数式を設定した。これらがセル I9、K9 と小数点以下5桁のレベルで一致したのは、前回の Python スクリプトと用いて計算した場合と同じだった。

参考のため、前回エントリー に示した計算グラフを再掲する。

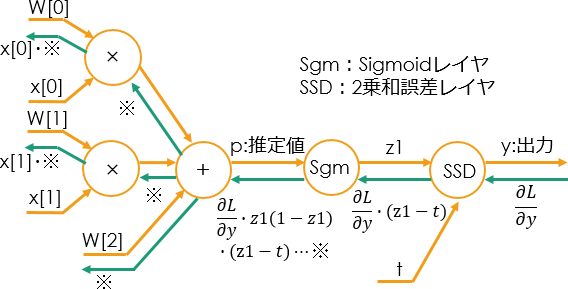
つまり、もう一度短く整理すると、

シグモイドを微分するには、z1(1-z1) を掛ければいいのだ。

2乗和誤差を微分するには、(z1-t) を掛ければいいのだ。

両者の合成関数を微分するには、z1(1-z1) と (z1-t) を掛ければいいのだ。

それはわかっているはずなのだが、なんだろうこの「何をやってるんだ」感は？ 合成関数の微分法の公式の導出を、もう一度復習すればいいのだろうか？ それもわかっているつもりなのだが…

念のため OR ゲートについて、さらに計算してみた。

入力データを0、1、教師データを1とした場合の結果。

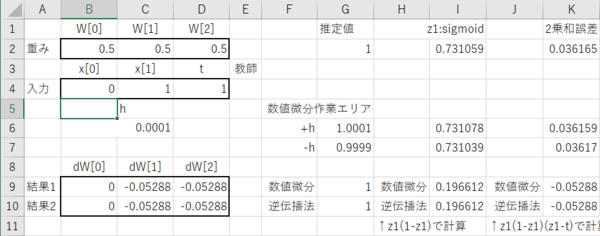
入力データを1、0、教師データを1とした場合の結果。

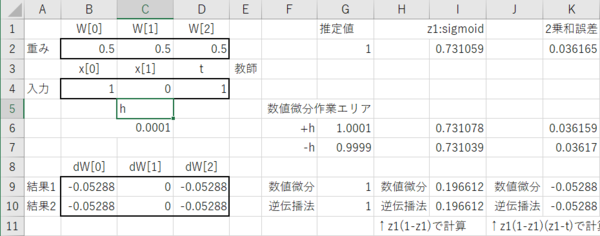
入力データを1、1、教師データを1とした場合の結果。いずれも前回の Python スクリプトで計算した結果と一致した。

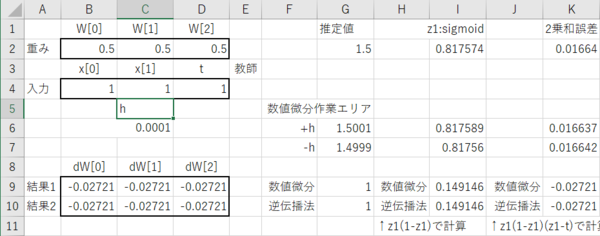
なんかどっかいっぱい間違いをやらかして、間違い同士がたまたま偶然うまく相殺し合って、あたかも正しい値が得られているように見えるだけで、実は全部間違っていた、なんてことはないよね？ ね？（誰に訊く？

この項続く。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装