「後編」で完結させられなかったので、本稿を書きました。
元のパズル「王様と7人の大臣と不貞なその配偶者」を、次のように改変する。
図示しやすくするためと、やろうと思えば教室などで実演できることを目指してである。
元のパズルとの同値性は、満たされているはずだ。
先生がパズルのマスター、生徒がパズルのプレイヤーである。7人の生徒に、ちょっと目をつぶってもらって先生が紅白帽をかぶせる。
個々の生徒には、他の6人がかぶっている帽子の色は見えるが、自分がかぶっている帽子は見えない。
最低誰か1人は赤い帽子をかぶっているとして、生徒に自分のかぶっている帽子の色を当てさせることはできるだろうか?
赤い帽子をかぶっているのが1人の場合は…

もし自分以外の全員が白い帽子をかぶっている生徒がいれば、その生徒は自分が赤い帽子をかぶっていると判断することができるので、それを自己申告すればいい。
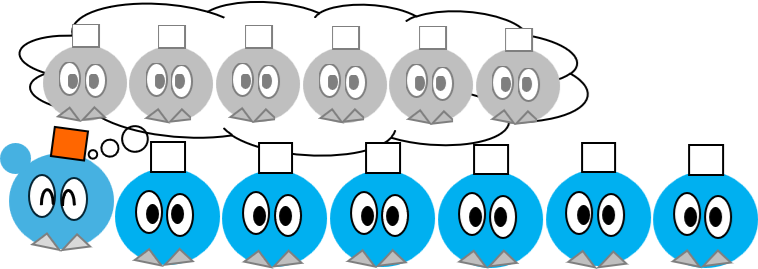
それを受けて他の生徒は、自分が白い帽子をかぶっていることがわかるのである。

では生徒が目を開けたとき、赤い帽子をかぶっている生徒が1人見えた場合は、どうすればいいだろう?
自分が白い帽子をかぶっていて、7人のうち1人だけが赤い帽子をかぶっているケースと…
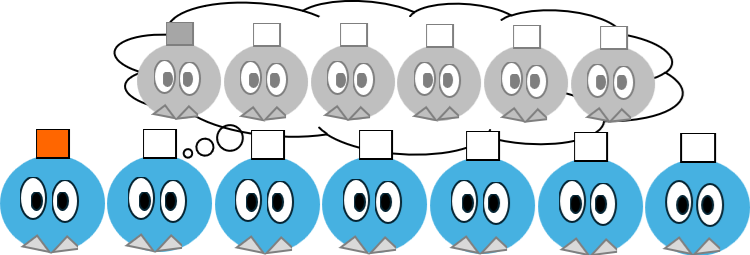
自分も赤い帽子をかぶっていて、7人のうち2人が赤い帽子をかぶっているケースがある。
この2つのケースは、何かヒントがないと区別できない。
弊ブログはアフィリエイト広告を利用しています
そこで先生は、こんなヒントを出すことにする。
先生はベルを用意し、一定時間ごとにチンと鳴らす。
最初のベルが鳴るまでを1ラウンド、2度めのベルが鳴るまでを2ラウンド、n度目のベルがなるまでをnラウンドと呼ぶことにする。
ボクシングの1ラウンドは3分だが、3分は長すぎるので1分ほどでいいと思う。30秒でもじゅうぶんじゃないだろうか?
そして1ラウンドごとに「自分の帽子の色がわかった人、手を挙げて」と尋ねる。
赤い帽子をかぶっている生徒が1人の場合は、その生徒が判断を間違えなければ、1ラウンド目で手を挙げるはずである。

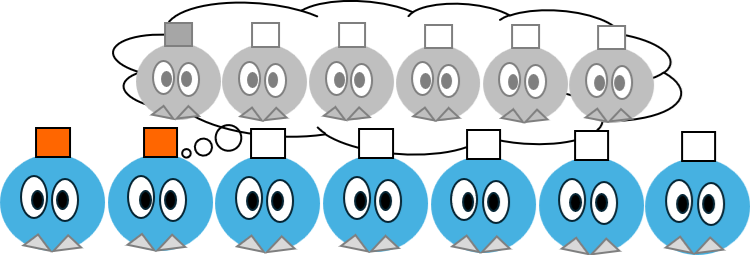
このヒントによって、赤い帽子をかぶっている生徒が2人の場合も、赤い帽子をかぶっている生徒は自分が赤い帽子をかぶっていると判断できるようになる。
もし自分に見えている赤い帽子をかぶっている生徒が1人で、1ラウンド目で手を挙げる生徒がいなければ、自分も赤い帽子をかぶっていると判断することができる。
なんとなれば、1ラウンド目で手を挙げた生徒がいなかったことにより、赤い帽子をかぶっている生徒が1人だけである可能性がなくなったからだ。
だから2ラウンド目で、すなわち2番目のベルが鳴る前に手を挙げればいい。

2人の生徒が「自分は赤い帽子をかぶっている」と申し出れば、そして彼らの判断が間違っていなければ、残りの生徒は自分がかぶっている帽子が白だとわかる。

ベルの音は、元のパズル「王様と7人の大臣と不貞なその配偶者」の朝刊に相当する。
1ラウンドは、元のパズルの1日に相当する。
同様に3ラウンド目では、もし自分に見えている赤い帽子をかぶっている生徒が2人で、1ラウンド目と2ラウンド目で申し出る生徒がいなければ、自分は赤い帽子をかぶっていると判断することができる。
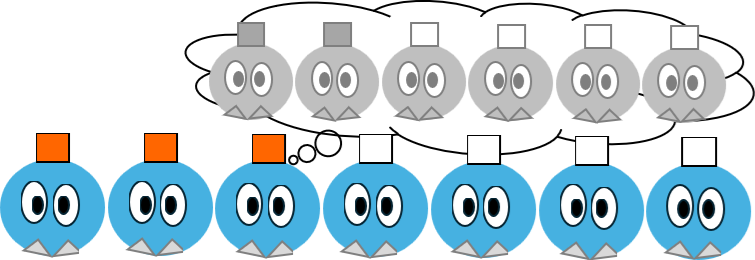

以下、nラウンド目で、もし自分の目に映っている生徒のうち n-1人が赤い帽子をかぶっていれば、自分は赤い帽子をかぶっていると判断することができる。
だから、もし6人が赤い帽子をかぶっていれば、そのことは6ラウンド目で判明し…
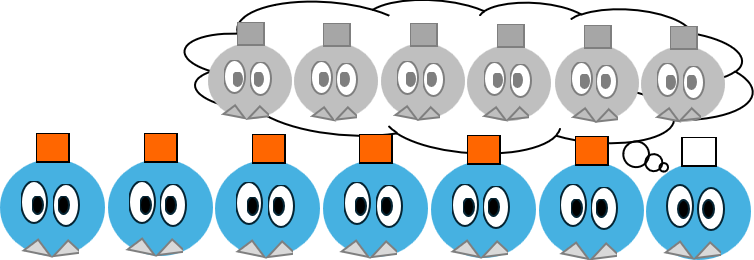

7人全員が赤い帽子をかぶっていれば、7ラウンド目でそれが判明する。
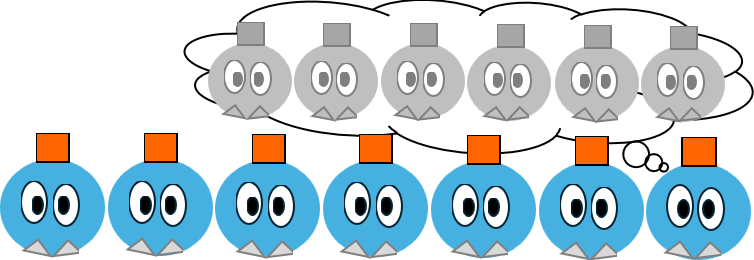

これは元のパズルで、7日目に7人の大臣宅で同時に惨劇が起きることに対応する。もし「40人の貴族と40人の従者」であれば、40日目に従者が悪者であることが判明する。つまり、導かれる結論は同じなのだ。
しかし「前編」で示した解法は大臣が1人~7人のケースを順に検討したが、本編の解法は赤い帽子をかぶっている生徒(配偶者が不倫をしている大臣)1人~7人のケースを順に検討している点が異なる。生徒or大臣の人数は、最初から7人なのだ。
考え方自体は「前編」に示したメタ思考と似ていなくもないが、赤い帽子をかぶっている生徒が1人であるケースから7人であるケースまですべてに対応している(参加者の全員が自分がかぶっている帽子の色が判断できる)ことと、数学的帰納法らしきものは用いているが再帰呼び出し(リカーシブ)ではなさそうであること、そして1ラウンドごとに使用される仮定が1つであることから(数学的帰納法において、仮定は「n-1 のときに成立している」だけだったはず)、推論に安心感があるように思うのですが、いかがでしょうか。
ご指摘歓迎。
つか、誰かもう同じこと考えている人、とっくにいそうだな。100円ショップに行けばゲームグッズがあったりして。
弊ブログはアフィリエイト広告を利用しています
ところで、このシリーズのオチを2通り思いついた。
一つは、"完全に論理的な存在"(Perfectly Logical Being:PLB) であるガッシュ伯爵を含む7人の大臣たちが、ロジックの脆弱性に気づき自分たちの奥方に手を下すことなく、また王様もそれを認めたと仮定すると、大臣たちが和解したことによりナーナッパ王国はさらなる発展を遂げたというエンドと…

あるいは大臣たちは心ならずも配偶者に手を上げざるを得なかったとして、それがあとで濡れ衣だったと判明したとして、さらに王様は悲劇の原因を作ったことを認めなかったと仮定すると、大臣たちは一致団結して王制を打倒しナーナッパ国は共和制に移行するというエンドを考えた。
いずれも2つ以上の仮定を含むため、どちらがより正しいかは証明できない。

追記:
本稿で完結と言いつつ、姉妹編を書きました。もしご興味をお持ちいただけましたら、ご笑覧願います。
弊ブログはアフィリエイト広告を利用しています