前回です。
1月19日付拙過去記事「【論理パズル】王様と7人の大臣と不貞なその配偶者(後編)」中に書いた "「死刑囚のパラドックス」に対する新しい解釈" というのを、改めて書いてみる。ただし、期間を3日に短縮する。
王様「お前の処刑は、3日後の日曜日までに行われる。だが、いつ死刑が執行されるかは知らされない」
もし土曜までに死刑が執行されていなければ、死刑が執行できるのは日曜日しかない。すると王命の後半に矛盾が生じる。だから日曜日に死刑を執行することは、できない。
1月19日付拙記事のイラストを再掲する。

そうすると、もし金曜日までに死刑が執行されていなければ、土曜日にも死刑を執行することはできない。なんとなれば、前段により日曜日に死刑が執行できないのだから、土曜日に死刑が執行されることがわかってしまうからである。
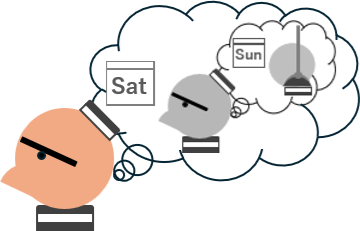
そうすると、金曜日にも死刑が執行できない。なんとなれば、前段により土曜日に死刑が執行できないのだから、金曜日に死刑が執行されることがわかってしまうからである。
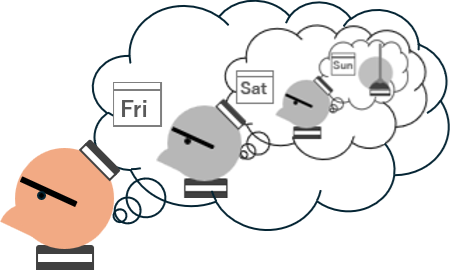
この推論に対して、登場人物の死刑囚に次のような反省をさせた。
金曜日の推論に着目すると
1. もし金曜日に死刑が執行されないと仮定すると
2. もし土曜日に死刑が執行されないと仮定すると
という2つの仮定を用いて、
∴ 日曜日に死刑が執行される
という結論を導いている。
もしこの結論が矛盾を生じるならば、仮定1. と2. のどちらが否定されることになるだろうか?
「金曜日に死刑が執行されるか、土曜日に死刑が執行されるか、どちらかである」という結論しか導けないのではなかろうか? 推論はここで停滞し前進しないのだ。
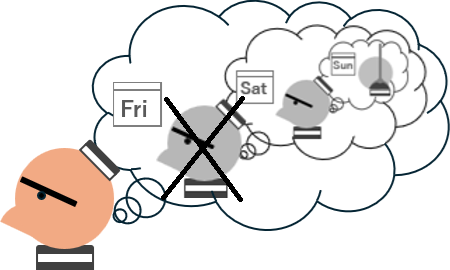
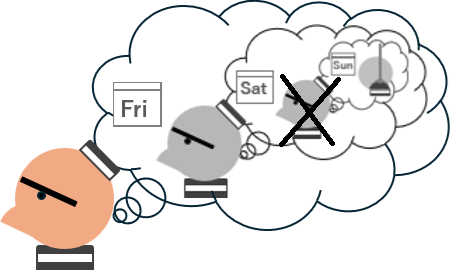
同じことを「抜き打ちテストのパラドックス」に対して繰り返してみよう。
教員が生徒に告げた。やはり期間を3日に短縮するため、火曜日に宣言したことにする。
教員「3日後の金曜日までに、抜き打ちテストを行う。だが、いつテストを行うかは知らされない」
死刑囚のパラドックスも「金曜日まで」と揃えておけばよかった。このくらい勘弁してください。
金曜日に抜き打ちテストを行うことはできない。なぜなら金曜日にテストが行われることが、わかってしまうからだ。

そうすると、木曜日にもテストを行うことはできない。金曜日にテストができないから、木曜日にテストを行うしかないとわかってしまうからだ。

そうすると、水曜日にもテストを行うことはできない。木曜日にテストができないから、水曜日にテストを行うしかないとわかってしまうからだ。

この推論は、正しいのだろうか?
1. もし水曜日にテストが行われないと仮定すると
2. もし木曜日にテストが行われないと仮定すると
という2つの仮定を用いて、
∴ 金曜日にテストが行われる
という結論を導いている。
もしこの結論が矛盾を生じるなら、「水曜日にテストが行われるか、木曜日にテストが行われるか、どちらかである」という結論しか導けないのではなかろうか? 推論はここで停滞し前進しないのだ。
ここまでが「2つ以上の仮定を含むため、背理法的な結論が下せないのではないか?」という解釈のおさらい。
ただし「1つ目の仮定(最終日前日に処刑orテストが行われる)は、前段の推論で否定される」という反論がありうること、それに対して「前段の推論の結論は、後段の推論(最終日2日前すなわち金曜日or水曜日に処刑orテストが行われる)に適用できるのか?」という再反論がありうることも、再録しておこう。
これらのことは、私にとっては意外なことに「その1」で述べた「赤い帽子の問題」を合わせて考えると、より論点が明確になるように思われた。
さらに「伏せたトランプ」も合わせるとグラデーションになるのでは、ということも思いついた。
書いていて新しいことを思いつくとは、もくろみ通りだ!
弊ブログはアフィリエイト広告を利用しています
「赤い帽子の問題」は死刑囚のパラドックスや抜き打ちテストのパラドックスとは、どうも異なる構造を持っていると、前回の「その1」で述べた。
n人のプレイヤーが、自分の前にいるプレイヤーの帽子の色しか見えないように並ぶ。かぶせ手が赤い帽子1個と白い帽子nマイナス1個のうち、どれかを彼らにかぶせる。
もし赤い帽子をかぶせられたプレイヤーが「自分の帽子は赤だ」と申し出ればプレイヤーたちの勝ち、誰も申し出ることができなかったらかぶせ手の勝ちである。
プレイヤーが1人しかいない場合は、プレイヤー必勝かぶせ手必敗だ。赤い帽子1つしかないため、プレイヤーに赤い帽子をかぶせることしかできないからだ。

プレイヤーが2人の場合、やはりプレイヤー必勝かぶせ手必敗になる。後ろのプレイヤーに赤い帽子をかぶせたら、前(後ろから2番目)のプレイヤーが白い帽子をかぶっていることから、後ろのプレイヤーには自分が赤い帽子をかぶっていることがわかってしまう。
だが前のプレイヤーに赤い帽子をかぶせたら、後ろのプレイヤーが「自分が赤い帽子をかぶっている」と申し出ないことにより、前のプレイヤーには「自分が赤い帽子をかぶっている」とわかってしまうという次第だ。

さて、プレイヤーが3人の場合。
もし1番後ろにのプレイヤーに赤い帽子をかぶせた場合、彼は前の2人が白い帽子をかぶっていることにより「自分が赤い帽子をかぶっている」と申し出ることができる。
後ろから2番目(真ん中)のプレイヤーに赤い帽子をかぶせた場合、1番前のプレイヤーが白い帽子をかぶっているのが見えるのだから、前段の推論(プレイヤー2人の場合)と同様1番後ろのプレイヤーの申し出がなければ「自分が赤い帽子をかぶっている」と申し出ることができる。
しかし1番前のプレイヤーは、どうだろう? 後ろの2人が「自分が赤い帽子をかぶっている」と申し出なければ、自分が「自分が赤い帽子をかぶっている」と申し出ることができる。
だが現実には、プレイヤーが自分が赤い帽子をかぶっていると判断してそれを申し出るまでには有限時間のタイムラグが必要である。その分、不確実性が生じ、かぶせ手にも勝つチャンスが生じるのではないか。
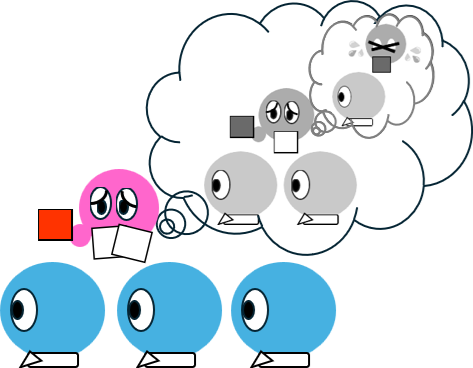
元ネタ『詭弁論理学』のようにプレイヤーが9人だったら、どうだろう? もっと大勢だったら、どうだろう? 前の方のプレイヤーに赤い帽子をかぶせたら、かぶせ手が勝つ可能性の方が高いと言えまいか。

ただし「その1」や 1月20日付拙記事 に書いた「一定時間ごとにベルを鳴らし、その都度申し出を促す」というヒントをつけ加えると、ふたたびプレイヤー必勝かぶせ手必敗に変化する。
「一定時間ごとにベルを鳴らす」というヒントをつけ加えた方が、赤い帽子の問題は死刑囚のパラドックスや抜き打ちテストのパラドックスと構造が近くなる。
それでもまだ違いがある。
赤い帽子の問題では、1番後ろのプレイヤーに赤い帽子をかぶせられないことが確定している。いっぽう死刑囚のパラドックスや抜き打ちテストのパラドックスで、最終日に死刑執行やテストの実施ができるかは、ルールからは読み取りづらい。あくまでグレーなのだ。
「伏せたトランプ」では、赤い帽子の問題と対照的に、最後の1枚がジョーカーであってもいっこうにかまわない。死刑囚のパラドックスや抜き打ちテストのバラドックスと並べると、鮮やかなグラデーションを構成しないだろうか。
n枚のトランプのうち、1枚だけがジョーカーである。このトランプを伏せて開いていく。何枚目がジョーカーか当てられるだろうか?
もしトランプが1枚だけだったら、それがジョーカーに決まっているから必ず当てられる。

だがトランプが2枚以上の場合、開き手は開いたカードがジョーカーかどうかは確率的にしか当てられなくなる。
これまで用いてきた「もし最後の1枚がジョーカーだったら」という推論は、無力になるからだ。
トランプが2枚の場合、もし最後のカードがジョーカーだと仮定する。そうすると1番上のカードはジョーカーではない。だがその仮定は、推論の役に立たない。「だから何?」ってやつで、1番上のカードがジョーカーかどうか判断する材料にはならない。

トランプが3枚の場合、前段までの推論は、1番上のカードがジョーカーがどうかの推論に役立つだろうか? 役に立たない。これまた「だから何?」ってやつで、1番上のカードがジョーカーかどうか、判断する材料にはならない。

素材はいらすとやさん トランプ | かわいいフリー素材集 からお借りしました。
まとめると、こうである。
赤い帽子の問題(一定時間ごとにベルを鳴らす)
一番後ろのプレイヤーが赤い帽子をかぶれるか? …かぶれない
プレイヤーが赤い帽子をかぶっていると申し出ることはできるか?…できる
死刑囚のパラドックス・抜き打ちテストのパラドックス
最終日に処刑orテストができるか?…あいまい、グレー
死刑囚or生徒が処刑日orテストの日を当てられるか?…確率的にしか当てられなさそうだがグレー
伏せたトランプ
一番下のトランプがジョーカーでありうるか?…ありうる
開いたカードがジョーカーか当てられるか?…確率的にしか当てられない
どうでしょう、グラデーションになっているという意味が、おわかりいただけるでしょうか?
死刑囚のパラドックスや抜き打ちテストのパラドックスにおいては、最終日に処刑orテストができるかがルールからは明確に読み取れないため、そのあいまいさが推論を重ねることにより増幅されると解釈することもできそうに思えてきた。
もし死刑囚のパラドックスや抜き打ちテストのパラドックスで、最終日に処刑orテストができるとルールで明確にしたら、どうなるだろう?
パズルの構造は伏せたトランプと全く同じになって、プレイヤーが確率的以外に処刑日orテストの日を当てることはできなくなる。
ではもし最終日に処刑orテストができないとルールで明確に定めたら、どうなるだろう?
この項、ひょっとしたら続けるかも知れません。ひょっとしたら尻切れトンボでこれで終わりにするかも知れません。
追記:
けっきょく続きを書きました。
弊ブログはアフィリエイト広告を利用しています